Глава 4 Векторные пространства 93

Глава 4. Линейные векторные пространства и подпространства

§ 4.1. Векторное пространство и его базис

Понятие линейного пространства Определение векторного пространства Базис векторного пространства Разложение вектора по базису Дополнение до базиса Переход к новому базису Свойства матрицы перехода

Понятие линейного пространства

Для дальнейшего изучения векторного анализа нам понадобится детализация понятия векторного пространства.

Определение. Множество элементов называется линейным пространством, если по некоторому правилу

1. любым двум элементам х и у из W поставлен в соответствие элемент из W, обозначаемый и называемый суммой элементов х и у;

2. любому элементу х из W и каждому числу поставлен в соответствие элемент из W, обозначаемый и называемый произведением числа на элемент х, причем справедливы следующие аксиомы:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) существует нулевой элемент 0 такой, что для любого ;

8) для каждого элемента х существует противоположный элемент –х такой, что .

Назовем эти два правила и восемь аксиом законами и аксиомами композиции в линейной алгебре. Элементы любой природы, удовлетворяющие всем этим условиям, по определению, образуют линейное пространство. Например, совокупность любых матриц размерами образует линейное пространство, поскольку для них выполнены оба правила и все аксиомы. Легко проверить, что совокупность геометрических векторов, например, трехмерного пространства также является линейным пространством.

Линейное пространство называется пустым, если оно состоит из нулевого элемента.

Изоморфизм линейных пространств.

Два линейных пространства называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие. Это соответствие для нас будет означать, что не только любой элемент из линейного пространства переходит в элемент из линейного пространства , но и сохраняются законы композиции, а именно: если и , то из и следует

1. ;

2. .

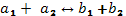Слово «элемент», а не «вектор» здесь приведено не случайно. Изоморфизм линейных пространств означает, что элементами линейных пространств могут быть не обязательно векторы, а, например, матрицы или что либо еще. Изоморфизм есть неразличимость линейных пространств различной природы с точки зрения свойств линейного пространства. Поэтому изучать линейные пространства можно на элементах простой структуры. Такими элементами мы будем брать наборы чисел (так называемые арифметические или координатные пространства). Называть эти наборы будем векторами и рисовать на бумаге (так называемые геометрические пространства).

Определение векторного пространства

Определение. Пусть для n-мерных векторов выполнены правила сложения и умножения на число, удовлетворяющие аксиомам линейного пространства. Тогда множество всех n-мерных векторов называется линейным векторным пространством и обозначается . Векторное пространство называется n-мерным, если среди множества его векторов найдутся n линейно независимых векторов, а любые векторов уже окажутся зависимыми. Число называется размерностью векторного пространства.

Например, среди бесконечного множества векторов, расположенных в одной плоскости, любые два неколлинеарных вектора являются линейно независимыми. Выберем какие-либо два неколлинеарных вектора и . Добавление 3-го вектора к выбранным двум делает их линейно зависимыми. Действительно, система уравнений, полученная из векторного равенства , будет иметь вид

.

Матрица коэффициентов имеет ранг, равный двум, откуда следует, что один из трех столбцов есть линейная комбинация двух других. Следовательно, размерность такого линейного векторного пространства равна двум.

Базис векторного пространства

Определение. Упорядоченная совокупность линейно независимых векторов -мерного векторного пространства называется базисом этого пространства.

Выбранные нами в рассмотренном выше примере в определенном порядке два неколлинеарных вектора составляют базис в двухмерном пространстве. Если векторы поменять местами, они также составят базис этого пространства, но другой. Если выбрать два других неколлинеарных вектора в определенном порядке, на них можно построить свой базис.

В общем случае пусть в -мерном векторном пространстве нам известны векторов . Количество способов выбора линейно независимых векторов из общего числа заданных не превышает величины

Кроме того, выбрав векторов, можно построить упорядоченных совокупностей. Тогда количество базисов в таком -мерном векторном пространстве может достигать величины

.

Если в векторном пространстве определен базис, другие векторы могут быть выражены через этот базис.

Разложение вектора по базису

(о разложении вектора по базису)

Каждый вектор линейного пространства можно представить и притом единственным образом в виде линейной комбинации векторов базиса.

◄Пусть векторы образуют базис в -мерном векторном пространстве. Возьмем произвольный вектор из этого пространства. Тогда совокупность векторов линейно зависима, т.е. найдутся такие не равные одновременно нулю числа , что

,

причем . Если бы выполнялось равенство , то хотя бы один из коэффициентов обязан быть неравным нулю. Но это противоречит определению линейной независимости векторов .

Разделим обе части уравнения на . Получим

. (1)

Равенство (1) есть линейная комбинация векторов базиса

, (2)

где . Представление вектора в виде линейной комбинации (2) является единственным в силу свойства 3 линейной зависимости векторов.►

Замечание. Равенство (2) называется разложением вектора по базису , а числа - координатами вектора в этом базисе. Считая компоненты вектора его координатами, можно представить вектор набором своих координат . Таким образом, упорядоченная совокупность действительных чисел (так определяется -мерный вектор) есть набор координат в определенном базисе некоторого -мерного пространства.

ПРИМЕР. Векторы заданы совокупностями действительных чисел

.

1. Найти размерность и базис линейного пространства, в котором заданы векторы.

2. Сколько базисов можно построить на данных векторах?

3. Задав базис, разложить остальные векторы по этому базису.

Решение. Составим матрицу из координат всех векторов

.

1. Ранг матрицы равен двум. Только два линейно независимых столбца содержатся в этой матрице. Остальные столбцы могут быть представлены как линейные комбинации двух выбранных линейно независимых столбцов. Следовательно, размерность пространства равна двум. Базисными векторами можно выбрать векторы , расположив их в следующем порядке: .

2. Число базисов, которые можно построить, не превышает величины

.

На самом деле их меньше. На векторах построить базис невозможно. Они коллинеарны и, следовательно, линейно зависимы: . Число возможных базисов равно 28.

3. Разложим векторы по выбранному базису .

Начнем с векторов и : ,

Представим векторы равенства как матрицы-столбцы

,

В матричной форме

,

или в сокращенной матричной форме

решение матричного уравнения имеет вид

или , .

Следовательно, , .

Действуя аналогично, для векторов и получим разложения , .

Дополнение до базиса

Вопрос о нахождении базиса - мерного линейного векторного пространства сводится к перебору наборов из произвольных векторов этого пространства и изучению ранга матрицы, составленной из координат выбранных векторов. При нахождении матрицы с величиной ранга соответствующие векторы можно брать как базис векторного пространства.

Если уже имеются линейно независимых векторов , возникают вопросы:

1. Можно ли создать базис в рассматриваемом векторном пространстве, опираясь на имеющиеся векторов и дополняя их другими векторами;

2. Если можно, как это сделать?

Ответ на первый вопрос дает следующая теорема.

(о дополнении до базиса)

Пусть векторы линейного пространства размерности линейно независимы, причем . Тогда в пространстве найдутся векторы такие, что совокупность векторов составит базис этого пространства.

◄ Пусть - произвольный вектор линейного векторного пространства . Представить любой вектор в виде линейной комбинации векторов нельзя, так как в противном случае совокупность векторов была бы базисом. Но в силу условия это невозможно. Поэтому должен существовать вектор такой, что дополненная система векторов будет линейно независимой.

Если , то эта система является базисом пространства .

Если , следует повторить рассуждения с векторами .

Следовательно, любая заданная совокупность линейно независимых векторов может быть дополнена до базиса векторного пространства. ►

Перейдем к методу дополнения линейно независимых векторов до базиса. Пусть даны векторы Составим из координат векторов матрицу, расположив для удобства координаты векторов по строкам:

.

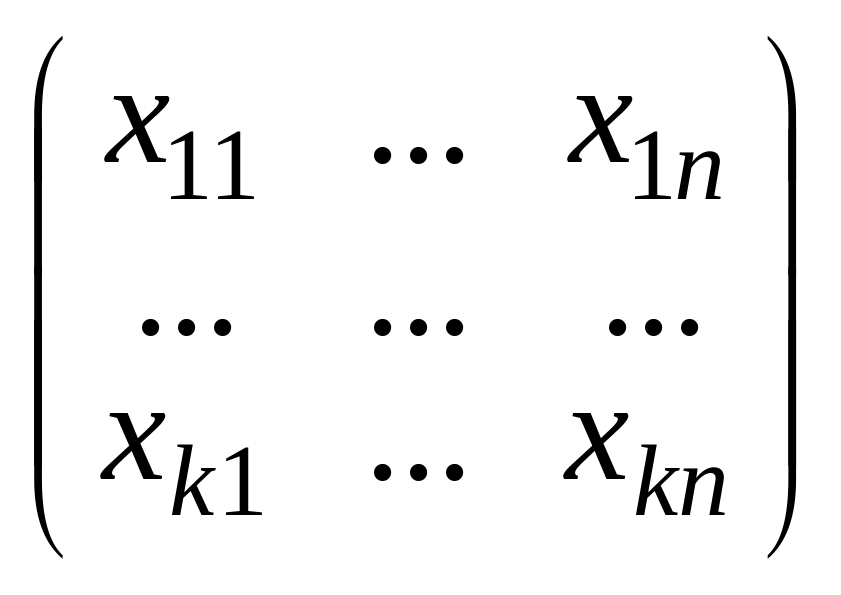Поскольку векторы линейно независимы и , элементарными преобразованиями строк матрица приводится к ступенчатому виду. Дополним полученную матрицу строками вида так, чтобы ранг новой матрицы, например, такой

стал равен . Тогда векторы вместе с векторами , координаты которых расположены в последних строках матрицы, составят базис - мерного линейного векторного пространства.

Замечание. Дополнение векторов до базиса произвольными векторами соответствующей размерности может не дать линейно независимых векторов.

ПРИМЕР. Дополнить набор векторов , 4-х-мерного векторного пространства до базиса этого пространства.

Р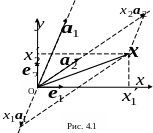 ешение. Если выбирать векторы с произвольными координатами, дополняя базис, среди них могут оказаться векторы, являющиеся линейными комбинациями данных векторов. Например, вектором нельзя дополнить базис, поскольку . Составим матрицу из координат данных векторов, приведем ее к ступенчатому виду и дополним ее двумя строками, чтобы она приняла вид

.

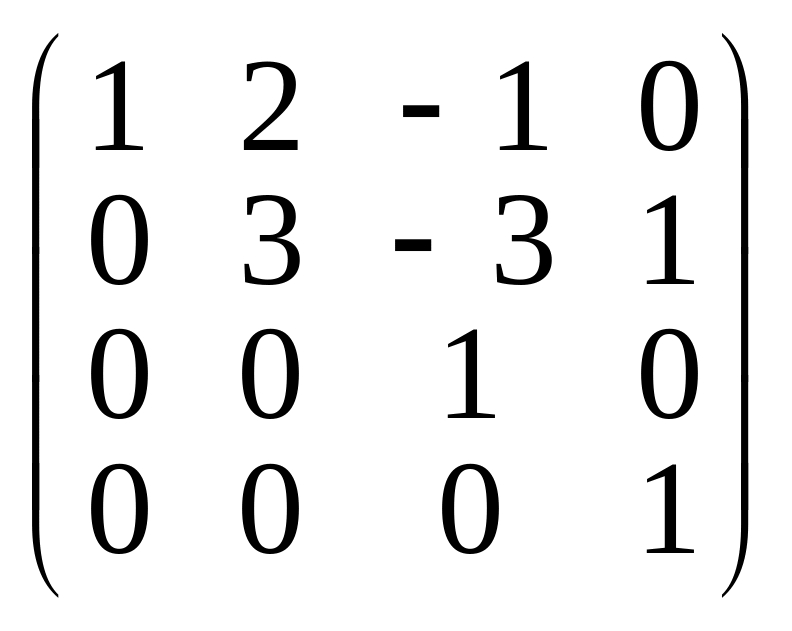Векторы , , , линейно независимы и составляют базис 4-х-мерного пространства.

В векторном пространстве не всегда удобно работать с уже заданным базисом. Рассмотрим, например, частный случай двухмерного векторного пространства – геометрическую плоскость, на которой определены длины и углы. Если вектор задан в базисе (рис. 4.1), имеет смысл перейти к другому базису , составленному из единичных и взаимно перпен­ди­­кулярных векторов. В новом базисе вектор имеет координаты . Возникает вопрос, как, зная коорди­наты вектора в старом базисе и взаимное расположение векторов старого и нового базисов, вычислить координаты вектора в новом базисе.

ППереход к новому базису

усть и - старый и новый базисы линейного - мерного векторного пространства . Каждый из векторов нового базиса можно выразить через векторы старого базиса:

а также представить в матричной форме:

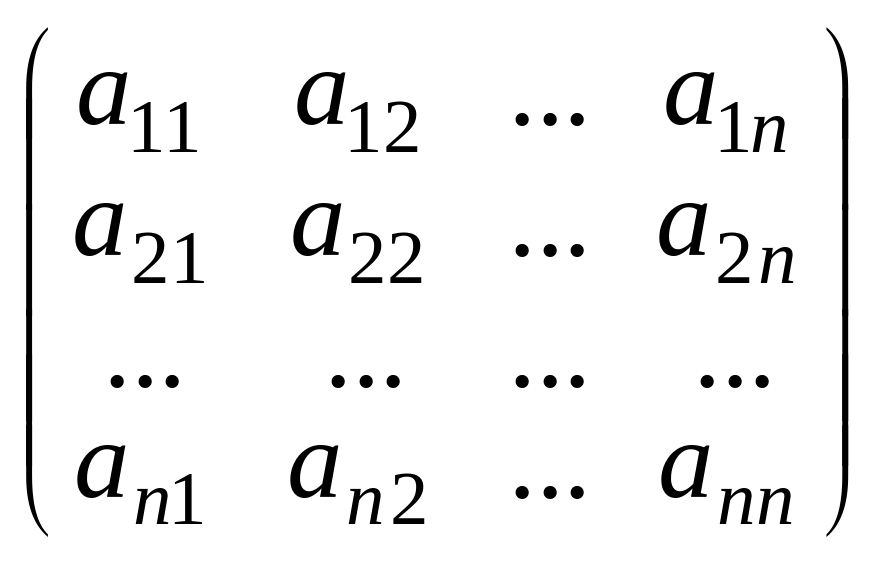= (3)

или в сокращенной матричной форме

,

где матрица А есть матрица координат старого базиса, расположенных по столбцам, В – матрица координат нового базиса, также расположенного по столбцам.

Матрица

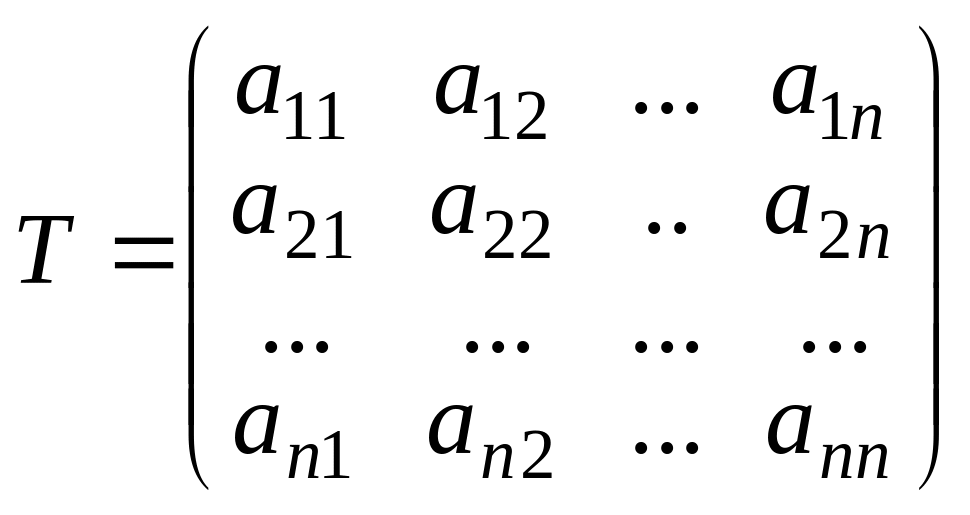
называется матрицей перехода от старого базиса к новому базису .

Замечание. Следует обратить внимание на то, что координаты разложения векторов нового базиса по старому базису располагаются в матрице перехода по столбцам.

Свойства матрицы перехода

1) Матрица перехода является невырожденной, т.е. .

Действительно, из равенства следует, что, один из столбцов матрицы Т является линейной комбинацией остальных столбцов. Тогда один из векторов есть линейная комбинация других векторов этого базиса, что невозможно.

2) Матрица перехода от нового базиса к старому имеет вид .

Умножив равенство (3) на справа, получим

= .

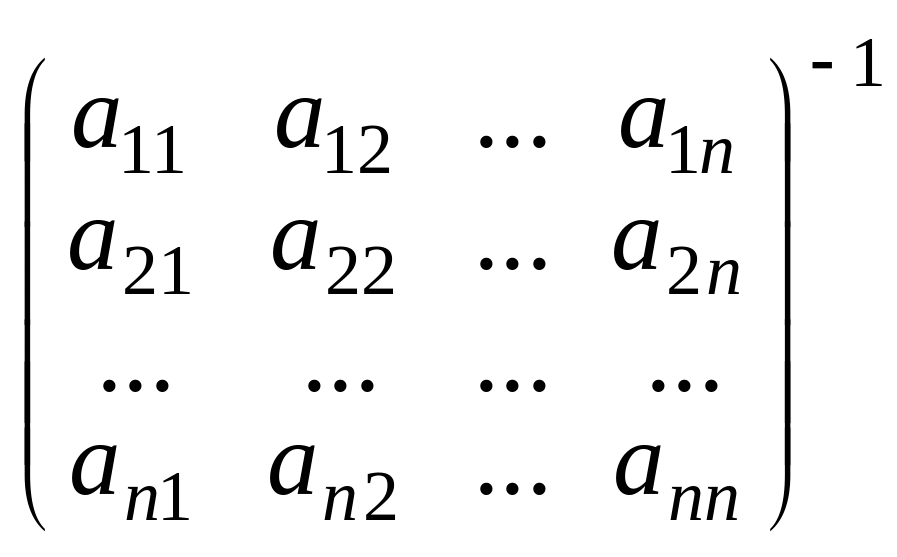3) Координаты вектора в разных базисах связаны матрицей перехода. Пусть некоторый вектор имеет координаты в старом базисе и координаты в новом базисе. Тогда

.

Подставив в это выражение разложения векторов по базису ,

получим

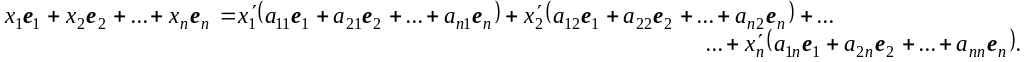
Перенесем все влево и сгруппируем слагаемые с одинаковыми сомножителями

Это равенство выполняется при условии, что все коэффициенты перед равны нулю. Следовательно,

В матричной форме или .

Координаты вектора в новом базисе выражаются через координаты вектора в старом базисе:

.

В развернутой матричной форме .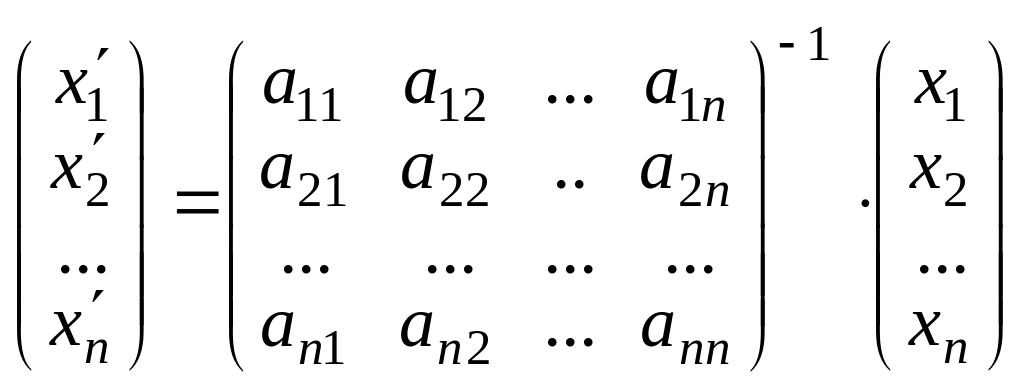

ПРИМЕР. Векторы , , , заданы своими координатами в старом базисе . Выразить координаты вектора в новом базисе .

Решение. Матрица перехода от старого базиса к новому базису имеет вид

.

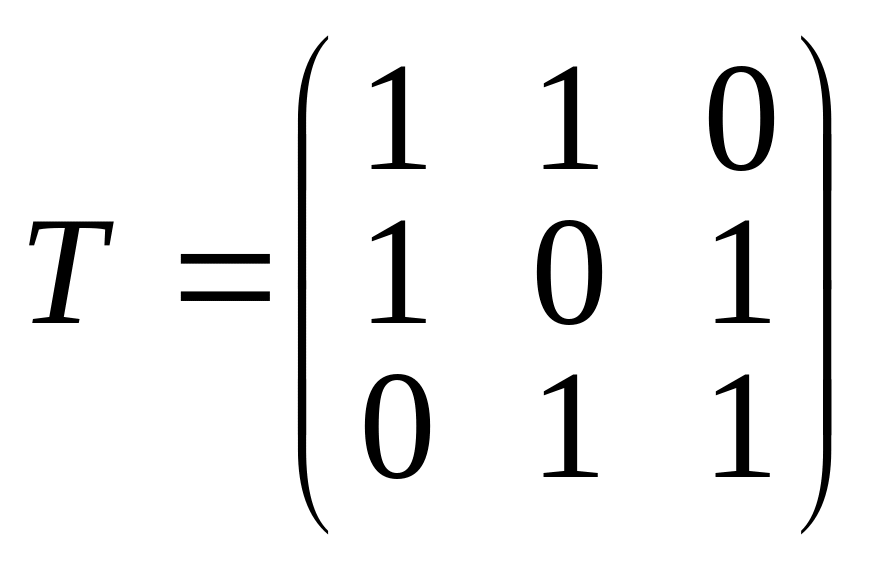Вычисляется обратная матрица: .

Координаты вектора в новом базисе:

.