§ 4.3. Линейные многообразия

Понятие линейного многообразия Способы задания линейного многообразия Свойства линейного многообразия Размерность линейного многообразия Арифметические операции над линейными многообразиями

Понятие линейного многообразия

При рассмотрении примеров линейных подпространств, было указано, что в геометрическом пространстве векторов пространства каждая прямая и каждая плоскость, проходящие через начало координат, определяют линейное подпространство. Прямым и плоскостям, не проходящим через начало координат, соответствует в линейной алгебре новый математический объект – линейное многообразие.

Пусть - линейное пространство, - некоторое его подпространство, содержащее векторы , (9)

- некоторый вектор из пространства . Все векторы считаются отложенными от начала координат. Множество всевозможных векторов вида , где вектор есть любой вектор из множества векторов (9) или любая их линейная комбинация, называется линейным многообразием и обозначается . Линейное многообразие, очевидно, получено сдвигом подпространства на вектор (рис. 4.5). Вектор называется вектором сдвига, подпространство - направляющим подпространством линейного многообразия .

Линейное многообразие обращается в линейное подпространство , когда вектор сдвига .

Пусть линейное подпространство - это совокупность всех векторов, лежащих на прямой, которая проходит через начало координат (рис. 4.5). Положим один из этих векторов равным . И пусть вектор . Тогда линейное многообразие состоит из множества векторов , , концы которых лежат на прямой, полученной сдвигом исходной прямой на вектор .

Способы задания линейных многообразий

Линейное многообразие может быть задано с помощью векторов следующим образом: задается базис векторного подпространства и вектор сдвига .

Другой способ задания - посредством системы неоднородных линейных уравнений. Множество решений неоднородной системы линейных уравнений является линей­ным многообразием. Обоснуем это утверждение. Напомним, что общее решение системы линейных уравнений склады­вается из общего решения однородной системы и базисного (частного) решения неодно­родной системы . Общее решение однородной системы есть линейная комбинация фундамен­таль­ного набора решений (ФНР), задающего некоторое линейное подпространство . Линейная комбинация ФНР плюс базисное решение есть общее решение системы неоднородных линейных уравнений. Поэтому линейное многообразие можно представить как множество решений некоторой в общем случае неоднородной системы линейных уравнений .

Свойства линейного многообразия.

1. Вектор сдвига принадлежит линейному многообразию.

◄Линейное подпространство содержит нулевой вектор: . Поэтому в суммах векторов содержится вектор .►

2. Вектором сдвига, принадлежащим линейному многообразию, может быть любой вектор этого линейного многообразия.

◄Пусть . Возьмем произвольный вектор . Тогда существует вектор такой, что , причем . Найдем сумму подпространства и вектора .

.

Получим то же линейное многообразие .►

3. Линейное многообразие определяется однозначно по известным подпространству и вектору сдвига .

◄Предположим, что существует еще одно линейное многообразие , построенное на линейном подпространстве , сдвинутом на вектор . Выберем базис в подпространстве . Любой вектор из линейного многообразия может быть представлен в виде линейной комбинации векторов базиса линейного подпространства и вектора сдвига

.

Точно также, в виде линейной комбинации можно представить любой вектор из линейного многообразия : ,

где . Но тогда вектор , а вектор . Векторы и - это произвольные векторы из линейных многообразий и . Следовательно, = .►

Размерность линейного многообразия

Определение. Размерностью (рангом) линейного многообразия называется размерность линейного подпространства :

Если линейное подпространство состоит только из нулевого вектора, то . Такое линейное многообразие имеет размерность , называется 0-мерным линейным много­образием (ранг равен нулю) и геометрически соответствует точке (конец единственного вектора ).

Если линейное подпространство , т.е. состоит из векторов, лежащих на одной прямой, то линейное многообразие называется одномерным. Его ранг равен единице. Геометрическая интерпре­тация многообразия – прямая (концы всех векторов лежат на прямой), не проходящая через начало координат.

Линейное многообразие, полученное из подпространства, состоящего из векторов плоскости, называется двумерным. Его геометрический образ – плоскость.

В –мерном векторном пространстве линейное многообразие размерности называется гиперплоскостью, а размерности , где , - k-мерной плоскостью.

Подобно прямым или плоскостям линейные многообразия могут пересекаться, скрещиваться, быть параллельными. Вводится также операция проектирования одного линейного многообразия на другое. Об этом подробнее в (9).

Операции с линейными многообразиями и их взаимное расположение.

1. Сумма двух линейных многообразий и есть линейное много­образие, определяемое по следующему правилу:

.

В частном случае при имеем

2. Пересечение двух линейных многообразий и есть линейное многообразие, вычисляемое по правилу

,

где .

2. Умножение линейного многообразия на число порождает новое линейное многообразие , определяемое так:

.

2. Параллельность двух линейных многообразий и означает, что направляющее подпространство одного из них содержит направляющее подпространство другого:

, если или .

2. Скрещивание двух линейных многообразий и имеет место в том случае, если они не пересекаются и не параллельны.

ПРИМЕР 1. Линейное многообразие задано системой линейных уравнений

Найти линейное подпространство и вектор сдвига такие, что .

Решение. Составим расширенную матрицу из коэффициентов и свободных членов системы уравнений и преобразуем ее, используя метод Гаусса.

 .

Вернемся к системе уравнений, взяв свободными переменными

.

Выделим фундаментальный набор решений (ФНР)

.

Линейно независимые векторы составляют ФНР, а, следовательно, базис подпространства . Любой вектор можно представить в виде . Вектор сдвига есть вектор .

ПРИМЕР 2. Линейное многообразие имеет вид

, где , , , .

Представить линейное многообразие в виде системы линейных уравнений.

Решение. Линейное многообразие есть множество векторов вида или в координатном виде .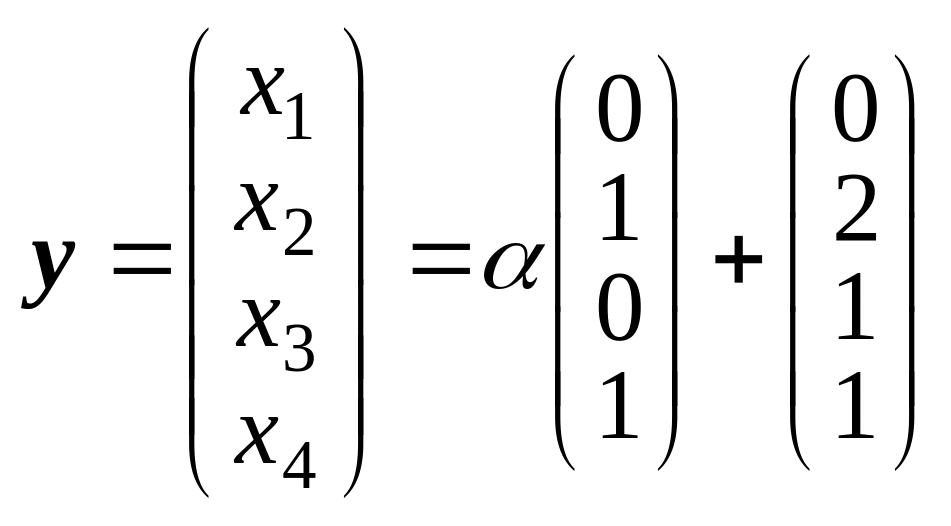

Перепишем систему уравнений относительно переменной , выделив столбец свободных членов.

.

Представим систему матрицей коэффициентов и воспользуемся методом Гаусса

  .

Система совместна при условии, что ранг матрицы коэффициентов равен рангу расширенной матрицы (теорема Кронекера-Капелли).

Следовательно, или

Линейное многообразие записано в виде системы неоднородных линейных уравнений.

Рассмотрим вопросы взаимного расположения линейных многообразий. Начнем с простого примера.

ПРИМЕР 3. Пусть в трехмерном линейном векторном пространстве заданы два двухмерных многообразия

где и

, где

Найти пересечение линейных многообразий .

Решение. Произвольный вектор , принадлежащий как одному так и другому линейному многообразию, может быть представлен в виде

(10)

или

,

где – координаты вектора в базисах направляющих подпространств линейных многообразий. Для удобства перепишем матричное уравнение так

Чтобы найти , составим расширенную матрицу и преобразуем ее методом Гаусса-Жордана

,

откуда следует . Подставив в равенство (10), получим

.

Следовательно, две двухмерные плоскости пересекаются по прямой ( ). Такой вывод можно сделать по виду преобразованной методом Гаусса-Жордана расширенной матрицы. Во второй строке 2-го и 3-го столбцов матрицы стоят отличные от нуля цифры. Значит, существует только одна независимая переменная, например, . ФНР содержит одно решение (один вектор). Этот вектор составляет базис подпространства размерности один, являющегося пересечением направляющих подпространств линейных многообразий.

Возможны другие варианты решений для двух плоскостей в трехмерном пространстве.

Пусть преобразованная матрица имеет вид

.

Значок поставлен в позициях, содержащих любое число. Если на пересечении последних столбца и строки стоит единица, решений нет (линейные многообразия не пересекаются ). Кроме того, поскольку зависят от , ФНР будет содержать два независимых решения (два вектора). Они составят базис двухмерного подпространства. При наличии единицы в последней строке последнего столбца двухмерные плоскости параллельны.

Если на пересечении последних столбца и строки стоит нуль, решения существуют (двухмерные плоскости пересекаются по плоскости, т.е. совпадают, .

Замечание. В преобразованной методом Гаусса-Жордана матрице в некоторых позициях могут стоять вместо единиц и нулей другие числа. Метод исследования взаиморасположения многообразий остается справедливым, если выполнены два условия:

1. Ранг матрицы базиса направляющего подпространства линейного многообразия соответствует рангу матрицы, составленной из столбцов, у которых только в одной позиции по вертикали стоит единица.

2. Если все базисные векторы какого-либо подпространства, расположенные по столбцам, содержат нули в определенной строке, то соответствующая матрица с единицами только в одной позиции по вертикали должна содержать в этой строке нули.

ПРИМЕР 4. Рассмотреть все варианты взаимного расположения трехмерного и двумерного многообразий в пятимерном пространстве.

Решение. Перечислим существенно различные варианты:

1) , 2)

1а) Комбинация цифр в последнем столбце « » → . Многооб­ра­зия не имеют общих точек.

1б) Комбинация « » → . Многообразие включено в многообразие .

2а) Цифра в последнем столбце «1» → . Многообразия не имеют общих точек.

2б) Цифра в последнем столбце «0» → Многообразия пересекаются по прямой.

3) , многообразия пересекаются в точке.

4.4. Метрические пространства

Аксиомы метрического пространства Нормы метрического пространства Геометрическая интерпретация норм

Аксиомы метрического пространства

Векторное пространство называется метрическим, если задано некоторое правило, по которому каждой паре векторов ставится в соответствие некоторое число . Оно должно удовлетворять 3 аксиомам:

1. для всех и при .

2. для всех ;

3. для всех .

Это число , где и , называется расстоянием между векторами или нормой, а правило (функция двух векторов, формула) – метрикой. Метрику можно ввести по-разному. Докажем, что векторное пространство станет метрическим, если для любых x и y из положить .

Покажем, что выполняются аксиомы метрики. Действительно, из свойств нормы вытекает, что

1. , причем тогда и только тогда, когда .

2. .

3. .

Нормы метрического пространства

Модуль разности векторов может быть вычислен в координатах по-разному (разные нормы). В экономике наиболее распространены следующие:

1. евклидова норма: .

В частном случае расстояние между вектором и нулевым вектором есть норма вектора = .

2. октаэдрическая норма: .

Норма вектора в векторном пространстве с октаэдрической нормой есть величина

= .

3. кубическая норма: .

Норма вектора вычисляется по формуле

= .

Задавая по-разному модуль разности векторов в координатах, мы должны убедиться в том, что аксиомы метрики не нарушены. Проверим справедливость аксиом на примере евклидовой нормы.

1. Очевидно , причем при .

2. 3. Аксиома для метрики имеет вид

.

Пусть и . Тогда получим неравенство

,

которое называется неравенством треугольника. Докажем его.

Запишем неравенство в координатной форме

.

Для доказательства возведем обе части в квадрат и раскроем скобки. После упрощения получим неравенство в координатах, называемое неравенством Коши-Буняковского

.

Докажем его справедливость. Рассмотрим очевидное неравенство

,

г де параметр . Раскрыв скобки, приведем его к квадратному неравенству относительно .

.

Поскольку неравенство выполняется при всех , его дискриминант не положителен ( )

,

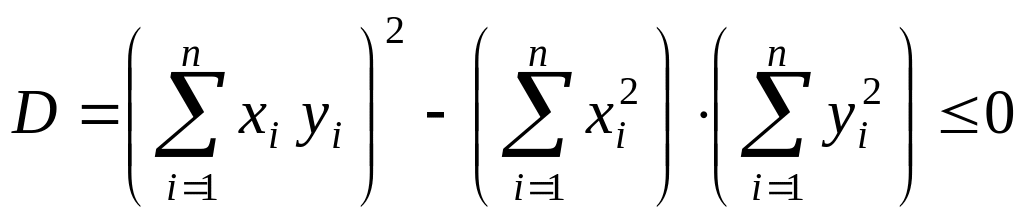о ткуда получаем неравенство Коши-Буняковского. Доказательство закончено.

Все аксиомы проверены.

Геометрическая интерпретация норм

Дадим геометрическую интерпретацию каждой нормы при и .

Для евклидовой нормы величина

есть расстояние между концами векторов и , указанное пунктирной линией (рис. 4.6). Эта величина соответствует расстоянию между двумя точками на плоскости в нашем физическом пространстве.

Октаэдрическая норма устанавливает расстояние между концами векторов

, (10)

п оказанное пунктирной линией на рис. 4.7. Наглядно представить себе это расстояние можно следующим образом. Представим себе, что мы находимся в той части города, где улицы пересекаются под прямыми углами (рис. 4.8). Рас­сто­яние от А до В мы можем пройти, двигаясь по улицам, по траектории АСВ или, например, по траектории АDВ. Но не мо­жем пройти по траектории АВ. Для нас расстояние от точки А до точки В вычисляется по формуле (10).

Расстояние, определяемое кубической нормой

,

представ­лено на рис. 4.9 пунктирной линией. Дадим экономи­ческую интер­пре­­та­цию этой нормы. Если вы можете заработать ден. единиц, но обязаны израсхо­довать ден. единиц, или, заработав ден. единиц, израсходуете при этом ден. единиц, ваш потребительский выбор, нацеленный на наибольшую выгоду, будет таким: максимум из двух величин или .

ПРИМЕР. Метрика линейного векторного пространства задается правилом . На координатной плоскости изобразить множество точек, для которых , если в метрическом пространстве принята 1. евклидова норма; 2. октаэдрическая норма; 3. кубическая норма. Ограничиться рассмотрением случая .

Решение. В двумерном векторном пространстве с евклидовой нормой и уравнение имеет вид или , с октаэдрической нормой - , с кубической нормой - . На координатной плоскости построим соответствующие графики (рис. 4.10)

Д ля понимания того, как выглядит объемное тело, если расстояния измерять, пользуясь разными нормами, введем понятие математического шара в метрическом пространстве. Математическим шаром с центром в точке и радиусом в трехмерном метрическом пространстве назовем множество .

В метрическом евклидовом пространстве это неравенство имеет вид

и представляет собой знакомый нам геометрический шар. Евклидова норма при описывает наше физическое трехмерное пространство.

В линейном векторном пространстве с октаэдри­ческой нормой математический шар

является более сложной фигурой. Изобразим ее на рис. 4.11, взяв центром точку и радиусом . Это октаэдр (восьмигранник). Поэтому и норма названа октаэдрической.

Математический шар в линейном векторном пространстве с кубической нормой

представляет собой куб, отсюда название нормы.