4. Применение магнитной термометрии

Прежде чем остановиться на свойствах конкретных пара­магнитных солей, рассмотрим, какое значение для термометрии имеют уравнение (2). Константы С, Θ и δ удается независимо вычислить с достаточ­ной точностью только для некоторых солей и получить связь между χ и Т в явном виде. Однако квантовая механика позво­ляет уверенно описать эти величины в широкой области темпе­ратур для ряда солей редкоземельных элементов и металлов переходной группы. Во всяком случае, измеряя парамагнитную восприимчивость при некоторых известных температурах и пользуясь уравнением (2), можно определить численные зна­чения констант и тем самым получить возможность интерполи­ровать, а в некоторых случаях и экстраполировать зависи­мость χ (Т).

Влияние анизотропии восприимчивости некубических кристал­лов в большинстве случаев можно сделать малым либо путем тщательной ориентации монокристалла, либо применяя порош­кообразный образец, хотя несферическая форма зерен порошка может вызвать нескомпенсированный магнитный момент и оста­точную анизотропию. Осуществить тепловой контакт с образ­цом из порошка проще, чем с монокристаллом, поэтому в маг­нитной термометрии применяется удобная форма образца неза­висимо от кристаллической симметрии соли.

Абсолютные измерения магнитной восприимчивости оказы­ваются очень трудными и в магнитной термометрии не приме­няются. Вместо этого измеряется взаимоиндуктивность двух ка­тушек, внутри которых находится образец. Она пропорцио­нальна восприимчивости образца. На ранних этапах развития магнитной термометрии для этой цели применялся мост взаимо­индукции Хартсхорна, однако в последнее время предпочтение отдается мосту, построенному на трансформато­рах отношений. В любом случае показания моста n можно представить в виде

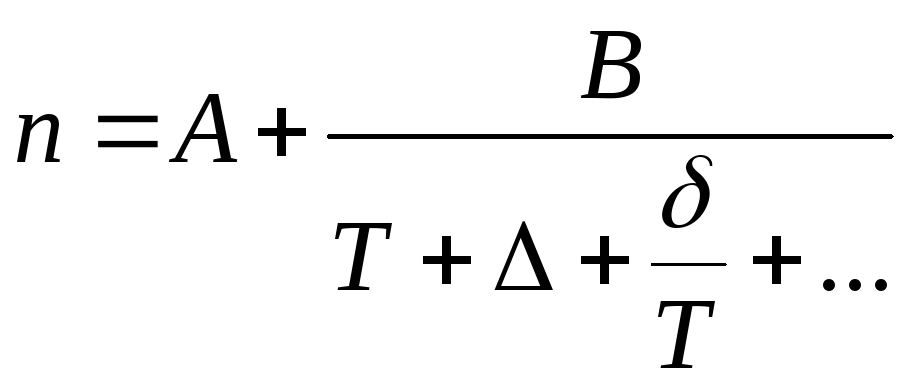(5)

где А — функция геометрических размеров катушек, которая включает в себя также не зависящую от температуры часть восприимчивости; В — функция геометрических размеров кату­шек и константы Кюри для данной соли; Δ учитывает свойства соли и форму образца; δ учитывает лишь свойства соли. Поскольку измеряемая величина n зависит от геометрических размеров катушек и данного образца, измеренные значения А, В и Δ описывают свойства только одного конкретного образца соли.

В магнитной термометрии широко применяются такие соли, как церий-магниевый нитрат (ЦМН), хромметиламмониевые квасцы (ХМК) и марганце-аммониевый сульфат (MAC). Пер­вая из них, ЦМН, Ce₂Mg₃(NO₃)₁₂24H₂O, применяется при тем­пературах ниже 4,2 К, так как чувствительность ее низка, а первое возбужденное состояние соответствует 38 К. ЦМН обладает гексагональной структурой и его магнитные свойства сильно анизотропны. Несмотря на это, величина Δ очень мала, приблизительно 0,27 мК. Восприимчивость в направлении, параллельном гексагональной оси, χ много меньше, чем вос­приимчивость в перпендикулярном направлении χ_. Восприим­чивость χ_ также мала, поскольку мал момент иона, J=1/2, а также вследствие того, что ионы в кристаллической решетке расположены на относительно больших расстояниях. Последнее обстоятельство приводит к тому, что ЦМН достаточно точно подчиняется закону Кюри и является одной из причин широкого применения этой соли для термометрии ниже 1 К.

Другие соли: ХМК, Cr(CH₃NH₃) (SO₄)₂12H₂O, и MAC, Mn(NH₄)₂(S0₄)₂6H₂O, могут применяться при более высоких температурах, чем ЦМН, поскольку первое возбужденное со­стояние для них соответствует очень высоким температурам. Ниже температуры перехода 164 К кубическая решетка ХМК перестраивается в орторомбическую. Магнитные свойства ХМК достаточно хорошо известны в связи с простотой ос­новного состояния, а ионы в узлах решетки расположены на относительно больших расстояниях, так что диполь-дипольное взаимодействие становится незначительным. Дюрье для ХМК нашел значения δ = 0,00279 К², Θ =12 мК и показал, что при температурах выше 1 К членами вида 1/Т² и более высо­ких порядков можно пренебречь. Таким образом, соль ХМК с успехом может применяться в магнитной термометрии для об­ласти температур выше 0,3 К. Теория магнитного состояния для MAC изучена значительно хуже ввиду гораздо более труд­ного для описания основного состояния, чем у ХМК. Пока не получено достаточно точных численных значений для Θ и δ, каждое из которых определяется экспериментально для кон­кретного образца. Тем не менее поведение индивидуальных образцов MAC довольно точно описывается уравнением (2) и, кроме того, константа Кюри для MAC в три раза выше, чем для ХМК. Большинство парамагнитных солей легко теряет кристал­лизационную воду, однако это не относится к ЦМН, с которой поэтому гораздо легче работать. Существует еще одна соль, свойства которой делают ее перспективной для магнитной тер­мометрии при температурах выше 4 К; это — метафосфат гадо­линия Gd(РОз)з. Эта соль не имеет кристаллизационной воды, а ее константа Кюри велика. Образец из такой соли можно приготовить как из порошка, так и из отдельного куска, по­скольку свойства ее изотропны.

На практике в магнитной термометрии достигнуты большие успехи. На рис. 2 и 3 схематически показана аппаратура, которую использовали Сетас и Свенсон для установления магнитной шкалы от 0,9 до 18 К. Эта шкала была принята за основу при установлении шкалы ПТШ-76. Образец соли, приготовленный из порошка, помещался в немагнитную нейлоновую капсулу, которая поддерживалась стержнем из кварцевого стекла, прикрепленным к медному блоку.

Рис.2. Схема криостата Сетаса и Свенсона для магнитной термомет­рии.

А — вывод электрических про­водов; В — промежуточный экран; С — термодатчик; D — экран блока; Е —ва­куумная рубашка из латуни; F — изме­рительные провода; G — тепловые ключи; Н — экран; I — стержень из кварцевого стекла;J — медные провода; K — катушка; L — нейлоновая ячейка; М — экран из «проволочной фольги»; N—радиационный экран из черной бу­маги; О — вакуумная рубашка из пирекса; Р—переход медь-пирекс; Q — высоковакуумная откачка; R—вакуум­ная рубашка трубки, передающей дав­ление; S — образец с солью; Т — гер­маниевый термометр сопротивления; U — медный блок; V — платиновый тер­мометр сопротивления; W—жидкий ⁴Не; Z — откачка паров ⁴Не.

Темпе­ратура блока измерялась германиевым и платиновым термо­метрами сопротивления. Медный блок имел полость, куда заливался жидкий гелий с последующей откачкой. Тепловой кон­такт между медным блоком и образцом обеспечивался набором тонких медных проволочек. Катушки располагались с наруж­ной стороны стеклянной вакуумной рубашки и поддерживались при постоянной температуре 4,2 К.

33 Г и.

Рис.3. Схема моста взаимоиндукции для измерения воспри­имчивости

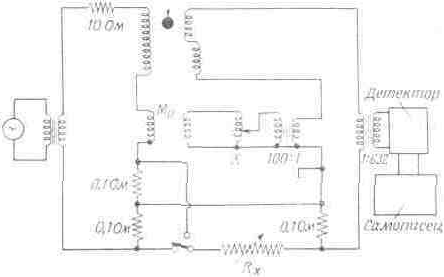
Взаимное расположение образца и катушек в течение серии измерений должно оставаться неизменным, так как от этого зависят константы в уравнении (5). Основные трудности, возникающие в магнитной термометрии, связаны с наличием малых температурных градиентов, зависящих от температуры, эффектов магнитной связи между различными частями криостата и движениями катушки и образца относительно друг друга. Для получения надежных экспериментальных результа­тов необходимо следить за чистотой образца и отсутствием магнитных примесей.

Согласно методике, которую применяли Сетас и Свенсон для получения магнитной температурной шкалы от 0,9 до 18 К, необходимо провести независимые серии температурных изме­рений в области от 18 до 34 К, чтобы определить константы А и В, а также в области от 0,9 до 2,6 К для получения Δ и . Значения Δ и  определялись первыми. Несмотря на про­стоту, методика в целом содержала ряд проблем, которые изло­жены в оригинальной работе. Сходная работа была выполнена Сетасом для значительно более широкой области темпера­тур. Он использовал две соли MAC и дополнительно октогидрат сульфата гадолиния Gd₂(SO₄)₃8H2O.

Воспроизводимость лучших магнитных термометров в широ­кой области температур выше 0,5 мК. Точность по отношению к термодинамической температуре зависит от точности, с ко­торой уравнение (5) описывает измеренную восприимчивость, от стабильности констант и точности, с которой они мо­гут быть измерены. Остаточные отклонения от термодинамиче­ской температуры связаны с отсутствием членов высокого по­рядка по 1/T в уравнении (5) .

Роль магнитной термометрии для исследования температурных шкал состоит в возможности найти их отклонения от термодинамической температуры.