3. Градуировка термометров на основе второго закона термодинамики

Некоторые соотношения, прямо основанные на втором законе термодинамики, можно использовать для однозначного определения абсолютной температуры, а именно

где ΔQ-количество тепла, приводящее к увеличению энтропии ΔS;U-внутренняя энергия;H=U+PV-BM– энтальпия.

На рис.1 показано применение соотношения T=ΔQ/ΔSдля градуировки магнитного термометра при адиабатическом размагничивании.

Пусть состояние парамагнитной соли соответствует точке 1 с Т=Т_iи В=В₁. Намагничивая соль изотермически, перейдём в точку 2, где Т=Т_iи В=В₁. Предполагается, что Т_i- температура_, которая известна по абсолютной термодинамической шкале. Затем образец термоизолируется и адиабатически полностью размагничивается; в результате он переходит в состояние, которому соответствует точка 2’, где температура имеет более низкое значение Т^*_f.

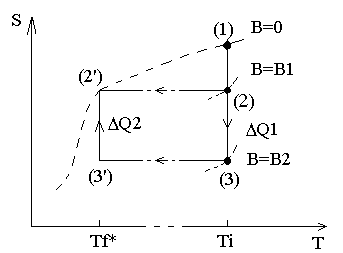
Рис.1. Определение связи между температурой Т и температурой магнитного термометра Т* термодинамическим методом.

Здесь Т^*_f– это температура по условной шкале, основанной на измерениях восприимчивости, причём предполагается, что закон Кюриχ=Λ/Т строго выполняется. Необходимо найти связь температуры Т=Т_fс истинной термодинамической температурой Т_f.

Далее система возвращается обратно в точку 2 и при поддержании строго постоянной температуры Т=Т_i(для чего применяется эффективный тепловой ключ) намагничивается от В₁ до В₂. При этом с помощью соответствующей методики, зависящей от условий эксперимента, необходимо определить количество тепла ΔQ₁, поглощаемое внешним резервуаром при намагничивании. Применяя уравнение (3), можно вычислить соответствующее значение энтропии ΔS₁=-ΔQ₁/ Т_iи таким образом, нанести точку 3 на (Т,S) - диаграмме.

Потом система теплоизолируется и адиабатически размагничивается, пока не будет достигнута точка 3’, где температура, также равная Т^*_f, как и ранее, определяется термометром, основанном на измерениях восприимчивости. После этого продолжается медленное размагничивание до тех пор, пока магнитное поле не уменьшится до нуля. Одновременно с этим к образцу подводится тепло с такой скоростью, чтобы его температура оставалась постоянной и равной Т^*_f. Пусть полное количество тепла, необходимое для этого изотермического процесса, равняется ΔQ₂. Так как энтропияSесть функция состояния, система снова приходит в точку 2’, в которой ΔS₂= ΔQ₂/Т_f, где Т_f- истинная термодинамическая температура, соответствующая Т^*_f. Замечая, что ΔS₁=-ΔS₂, находим, что Т_fможно определить из соотношения

Т_f= (ΔQ₂/ ΔQ₁) Т_i (4)

Если провести ряд размагничиваний, начиная с различных значений магнитного поля В, можно полностью определить зависимость Т от Т*.

Термодинамический метод градуировки прост в принципе, но практически имеет ряд ограничений. Трудно нагреть образец однородно и точно измерить приращение тепла ΔQ; кроме того, трудно достичь полной уверенности в том, что процессы размагничиания действительно протекают адиабатически. Несмотря на эти сложности и на то, что измерения весьма трудоёмки, термодинамический метод применялся для определения зависимости температуры Т от Т* для многих парамагнитных солей при низких температурах. Реальные измерения несколько отличаются от идеализированной процедуры, описанной выше.