1nikitin_a_ya_sosunova_i_a_analiz_i_prognoz_v_ekologicheskikh

38

4. Измерение связи между рядами

Степень связи между отдельными ВР часто характеризуют через нахождение коэффициента корреляции. Связь может быть прямой или обратной. Наиболее часто, используют коэффициент корреляции Пирсона /2, 6, 16/, который рассчитывается только для стационарных, нормально распределенных рядов по формуле:

зависимость между исследуемыми переменными. Однако всегда нужно помнить, что обсуждать степень связи имеет смысл только в случае статистического подтверждения ее наличия. Иными словами, даже если |r|>0,9 , но связь не значима, этот факт не дает оснований делать вывод о наличии корреляции между процессами.

Оценка значимости r проводится по Приложению 7. Число степеней свободы определяется как: df = n1 +2 n2 −2 .

Для вычисления r удобно использовать статистические программы, например, Excel. В меню «функция» с целью вычисления r вызывается команда «КОРРЕЛ», а дальше необходимо следовать инструкциям ее диалогового окна.

Применение корреляционного анализа следует сопровождать биологической интерпретацией полученных результатов, так как само наличие связи не является доказательством причинно-следственной обусловленности явлений /6/.

В случае ненормального распределения наблюдений в ВР для выявления связи между ними может быть использован ранговый коэффициент корреляции /2, 6,16, 22/. Однако, в Excel, в отличие от программы Statistica, нет его «автоматического» расчета.

Поскольку каждый ВР представляет процесс, формирующийся под действием множества различных переменных, то возникает задача изолированного измерения тесноты связи между отдельными рядами при фиксированном влиянии остальных.

39

Основой решения подобной задачи является построение матрицы парных коэффициентов корреляции (табл.4.1), с помощью которой наглядно представляется уровень связи между каждой из переменных в отдельности, когда значения влияния других факторов продолжает сказываться.

т.д.), то достаточно анализировать лишь верхнюю (над диагональю) или нижнюю части табл.4.1. Значения диагонали равны единице, в силу полной связи значений каждого ВР при коррелировании их самих с собой.

Для устранения влияния связи одних рядов на характер ее проявления между другими, рассчитывают частные коэффициенты корреляции первого, второго и так далее порядков /6, 16, 22/. Порядок связи указывает на количество фиксированных переменных, то есть в нашем случае рядов, влияние которых на исследуемый ВР статистически исключено.

Рассмотрим расчет частного коэффициента корреляции первого порядка между рядами А, B при фиксированном C. Для этого используется формула:

где rab, rbc, rac – парные коэффициенты корреляции, которые берутся из матрицы парных коэффициентов табл. 4.1.

Аналогичным образом рассчитываются и другие частные коэффициенты корреляции первого порядка (rbc.a, rac.b). Формулы расчета для коэффициентов более высокого порядка можно найти в работе /22 /.

Таким образом, мы оперируем уже двумя коэффициентами корреляции,

относящимися к исследуемым рядам А и В: парный rab и частный rab.c , которые

40

характеризуют степень связи между их уровнями. Первый коэффициент оценивает связь между рядами на фоне влияния фактора С. Второй (частная корреляция) – при исключенном влиянии С. Таким образом, частный коэффициент корреляции более точно характеризует степень линейной зависимости определенных рядов. Значимость величины частного коэффициента корреляции определяется по Приложению 7. Однако число степеней свободы в этом случае рассчитывается по формуле: df = n – 3 – k, где n – число пар в сравниваемых рядах, k – порядок вычисляемого коэффициента частной корреляции.

Частный коэффициент корреляции обладает всеми свойствами парного, которые уже рассмотрены выше.

Матрицу парных коэффициентов корреляции можно рассчитать в любой из компьютерных статистических программ. Так в Excel для этого необходимо: войти в диалоговое окно «Сервис», затем - «Анализ данных...» и, наконец, «Корреляция». Однако сами значения частных коэффициентов корреляции эта программа автоматически не рассчитывает. Для этого нужно либо, используя матрицу парных коэффициентов корреляции, самостоятельно провести расчеты по формуле (16), либо воспользоваться другой статистической программой, например, Statistica.

Множественный коэффициент корреляции характеризует степень линейной зависимости одного ряда от остальных, входящих в уравнение в качестве независимых переменных. Он изменяется от 0 до 1. Равенство его единице свидетельствует о функциональной связи исследуемого ряда с исследованными переменными модели. Равенство нулюоб отсутствии линейной зависимости между изучаемым процессом и другими параметрами.

Линейный множественный коэффициент корреляции вычисляется в Excel по команде «ЛИНЕЙН», а также в пакете «Анализ данных». Кроме линейного, можно рассчитать нелинейный множественный коэффициент корреляции. С этой целью используется опция «ЛГРФПРИБЛ» в диалоговом окне «функция» программы.

Ниже дана формула для расчета линейного множественного коэффициента корреляции в случае исследования трех рядов:

коэффициенты корреляции, взятые из матрицы табл.4.1. Остальные множественные

41

коэффициенты корреляции (rb/a,c и rc/a,b) рассчитываются по этой же формуле с соответствующими заменами обозначений.

Пример 8.

Рассмотрим связь между рядами, один из которых описывает динамику заболеваемости населения Иркутска клещевыми боррелиозами (ранее регистрировались как болезнь Лайма), а другой клещевым энцефалитом /14, 15/. Переносчиком обоих видов возбудителей является таежный клещ. Это позволяет предположить, что между уровнями заболеваемости этими инфекциями может существовать положительная корреляция. Однако ряд авторов полагает, что боррелии и вирусы вступают в определенные конкурентные отношения. В этом случае связь между рядами может отсутствовать или даже быть отрицательной.

Попытаемся самостоятельно исследовать проблему о характере связи между динамикой заболеваемости населения клещевым энцефалитом и клещевыми боррелиозами. А на основе полученных результатов сделаем вывод относительно наличия или отсутствия у возбудителей тяжелых заболеваний человека конкурентных отношений. Кстати, от характера выводов по этому вопросу в определенной мере зависит тактика их лечения и профилактики.

Исходные данные о заболеваемости приведены в табл.4.2. Причем, так как они получены на одной и той же выборке людей (населения Иркутска), то нет необходимости переводить значения заболеваемости в расчете на 1000 или 100 тысяч человек, как это обычно принято в медико-санитарных исследованиях. Однако, как выше указывалось, коррелируемые ряды должны быть стационарны и иметь нормальное распределение. Если не учитывать этих моментов и просто рассчитать коэффициент корреляции Пирсона между исходными рядами, то он равен 0,460 и является незначимым (см. Приложение 7). Но можем ли мы доверять такой его оценке? Ниже приведен порядок корректной процедуры расчета связи между двумя рассматриваемыми рядами с учетом характера распределения наблюдений и стационарности процессов.

Ряд КЭ не отвечает условию стационарности (о чем уже говорилось и ранее, см. рис.2 и Пример 5). Поэтому было проведено его преобразование к стационарному виду методом удаления тренда по аналитическому степенному уравнению: Υ = 55,44 * Χ0,4237 . Остатки, получившиеся после удаления тренда приведены в табл.4.2.

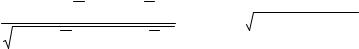
42

Их распределение с высокой долей надежности можно считать нормальным (С=3,05, см. Приложение 3).

Ряд заболеваемости населения клещевыми боррелиозами не содержит в себе явно выраженного нециклического тренда (значение критерия Стьюдента при сравнении последовательных групп равно всего 0,1 при 6 степенях свободы, Р>0.05, см. Приложение 2). Вместе с тем, он лишь с «малой надежностью» представляет выборку с нормальным распределением данных (С = 2,54, см. Приложение 3). К сожалению, преобразования уровней ряда, выполненные в соответствии с рекомендациями Приложения 4, путем нахождения обратной величины (1/Х) или логарифмирования существенно не меняют эту ситуацию (максимальное достигнутое С=2,56). Поэтому этот ряд мы оставили при анализе корреляций без дополнительных преобразований (табл.4.2). Расчитаем коэффициент корреляции Пирсона (14).

Таблица 4.2 Многолетняя динамика заболеваемости населения Иркутска клещевым

энцефалитом (КЭ) и клещевыми боррелиозами (КБ)

43

Для 10 сравниваемых пар значений связь существенна, так как при df =10-2=8 значимым считается коэффициент равный уже 0,632 (P<0,05 по Приложению 7). Таким образом, между временными рядами динамики заболеваемости населения Иркутска клещевым энцефалитом и клещевыми боррелиозами существует значимая положительная связь. Подобная корреляция вполне объяснима на основе известного факта распространения обеих болезней одним и тем же видом клещей. В то же время такая связь между рядами не подтверждает гипотезу о наличии конкуренции у возбудителей этих заболеваний. Конечно, реальная ситуация гораздо сложнее и существуют и другие доводы как за, так и против предположения о конкурентных взаимоотношениях вируса и боррелий. Однако наша цель была показать, как самое простое, но грамотное использование методов статистики помогает решать сложные научные проблемы.

44

5. Простые методы прогнозирования временных рядов

Одна из основных целей анализа ВР состоит в их прогнозировании /1, 8/. Существует множество статистических приемов и методов, используемых для решения этой задачи. Каждая статистическая компьютерная программа содержит определенный набор из них. Вместе с тем, выделить один метод в качестве наиболее «правильного» невозможно. Обусловлено это тем, что каждый из них лучше аппроксимирует ВР определенного типа, в разной степени отвечает целям того или иного эксперимента, техническим возможностям, уровню подготовки исследователя и т. д. Следовательно, возникает задача оценки адекватности выбранного метода прогноза. Решаться она может, в частности, при помощи оценки величины коэффициента детерминации и расчета критерия Дарбина-Уотсона.

Необходимо отметить и существование проблемы «несовместимости» понятий точности и надежности прогноза. Так, если мы поставим целью определить ожидаемые уровни исследуемого ряда абсолютно точно, то вероятность ошибки предсказания будет выше, то есть надежность прогноза меньше, чем при решении более скромной задачи. Например, можно с большой долей уверенности (надежности) определить, будет ли в ближайшее время наблюдаться потепление или похолодание, нежели спрогнозировать точное значение температуры воздуха. Обычно достаточной мерой надежности прогнозов в биометрии считается использование 90 % доверительного интервала (соответствующего в Приложении 2 десяти процентному (P<0,1) уровню значимости). В свою очередь точность прогноза можно оценить, рассчитав величину дисперсии ряда остатков, полученных путем исключения из исходных наблюдений их расчетных значений. Точность тем выше, чем величина дисперсии ниже.

Рассмотрим простейшие алгоритмы прогнозов ВР, охватывающие их основные типы: линейный тренд, циклические и сезонные колебания, а также комбинированные кривые. Более подробное изложение применения этих, а также других методов прогноза ВР можно найти в специальной литературе /1, 2, 7, 10/.

5.1. Прогноз по тенденциям развития ряда

Прогноз этим способом не требует получения дополнительной информации об изменении других факторов, влияющих на исследуемый ВР. Он весь базируется на анализе закономерностей поведения одного лишь исходного ВР в прошлом. Однако так как реальный ряд формировался под действием множества факторов, то метод, в неявном виде, учитывает все возможное многообразие условий существования зависимой переменной и ее реакции на них.

45

5.1.1.Метод парной линейной регрессии Наиболее простым способом прогнозирования можно считать перспективную

экстраполяцию с использованием уравнения парной линейной регрессии, где в качестве независимой переменной рассматривается фактор времени. Алгоритм выполнения прогноза включает в себя следующие этапы: 1. Доказательство наличия закономерного характера изменения наблюдений в исследуемом ряду (см. разд.2.2.1). 2. Аналитическое выражение имеющегося тренда в виде уравнения парной регрессии («статистически» выполнение первого и второго пункта может быть совмещено). 3. Проверка адекватности выбранной модели тренда исходным наблюдениям (см.

разд.2.3).

Уравнение парной регрессии является наиболее простым для проведения прогноза. Если мы получили иное аналитическое уравнение в качестве модели исследуемого процесса (см. 2.2.2.1, Пример 5), то в некоторых случаях лучше попытаться его преобразовать в линейное. Возможные варианты решения этой проблемы даны в Приложении 4.

Рассмотрим способ прогнозирования трендов, описываемых уравнением прямой линии:

где Υx - среднее значение исследуемого ВР при определенном значении факто-

ра времени; а – свободный член уравнения регрессии; b - коэффициент регрессии, который показывает, на сколько единиц в среднем изменится исследуемый ВР при изменении времени (t) на одну единицу его измерения. Знак при коэффициенте b соответствует направлению изменения зависимой переменной с течением времени.

Параметры уравнения регрессии находятся методом наименьших квадратов по формулам:

все обозначения даны выше.

46

Расчет параметров уравнения по формулам с использованием калькулятора является рутинной процедурой. Любая математическая компьютерная программа выдает уравнение сразу. Однако, для понимания логики прогнозирования по уравнению прямолинейного тренда считаем полезным сначала провести подобные расчеты вручную. Для этого можно воспользоваться Примером 9 или обсчитать собственные данные.

Для определения величины прогнозируемых значений наблюдений через время t необходимо в полученное аналитическое выражение тренда подставить соответствующие значения параметра времени. Однако любой прогноз содержит определенную ошибку и должен приводиться в работах вместе с доверительным интервалом:

(20),

где tα - табличное значение критерия Стьюдента (Приложение 2) для принятого уровня значимости и соответствующего числа степеней свободы; Sp – ошибка прогноза. В свою очередь ошибку прогноза определяют по формуле:

коэффициент, который зависит от типа тренда и периода упреждения (предсказания). Ошибка прогноза для уравнения линейной регрессии будет иметь следующий

где yt – фактические значения наблюдений; ηt - расчетные значения уровней ря-

да по линейному тренду; n - длина ВР, m - число параметров в уравнении тренда, без свободного члена, l - период упреждения. Причем время должно быть представлено рядом натуральных чисел от 1 до n.

Как и следовало ожидать, чем больше мы имеем исходных наблюдений (n), тем меньше поправочный коэффициент, а значит выше точность прогноза. Вместе с тем, чем более удален период времени на который делается прогноз ( l -больше), тем его точность становится ниже. Поэтому целесообразно уравнения прогноза периодически, по мере поступления новых данных об исследуемом процессе, корректировать путем пересчета их коэффициентов. Выполнить эту процедуру на компьютерах не сложно.

47

Следует отметить, что без учета изменения ошибки прогноза, связанной с периодом упреждения ( l ), экстраполяцию значений и расчет доверительного интервала прогноза можно легко проводить в Excel. Причем при малом упреждении будут получаться одни и те же значения. Для реализации линейного прогноза в Excel можно воспользоваться следующей последовательностью команд: «Сервис», «Анализ данных...», «Регрессия». В результате мы получим три таблички, содержащие материал по оценке надежности линии аппроксимации, величине свободного члена и коэффициенте наклона линии регрессии, а также значения их ошибок при определенном уровне значимости и др. параметры.

Пример 9.

Рассмотрим пример об изменении численности городского населения в России (табл. 5.1) /18/. Поставим задачу: построить уравнение регрессии, характеризующее динамику численности жителей в городах страны за 10 лет. Рассчитаем параметры линии регрессии (18) с помощью калькулятора по формулам (19) и (20), используя графы 5-7 и строку сумм табл.5.1. При этом получим уравнение:

y = 109,98- 0,2709x .

Теперь решим эту же задачу в программе Excel. Для этого воспользуемся приводимым ниже «по шаговым» алгоритмом анализа ВР.

1. Внесем данные из табл.5.1 в Excel. 2. Выделим курсором графу, отражающую численность населения. 3. Активизируем команду «Мастер диаграмм» на верхней панели программы. 4. Из появившегося диалогового окна выберем команду «график», а в ней активизируем пункт «график с маркерами». 5. Так как в данном случае в дальнейшем нам собственно график не потребуется, то сразу же дадим команду «построить график». Перед нами на экране монитора появится рисунок ряда. 6. Наведем курсор на получившуюся на графике кривую, отражающую характер изменения численности населения, и нажмем правую клавишу мышки.7. В появившемся меню выберем опцию «добавить линию тренда». 8. В раскрывшемся окне «линии тренда» выберем его тип - «линейный». 9. В этом же окне сделаем переход в пункт меню «параметры». 10. В диалоговом окне «параметры» с помощью мышки пометим команды, соответствующие пунктам «показывать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации (R2)». 11. Подтвердим компьютеру необходимость выполнить заданные установки.