
1nikitin_a_ya_sosunova_i_a_analiz_i_prognoz_v_ekologicheskikh
.pdf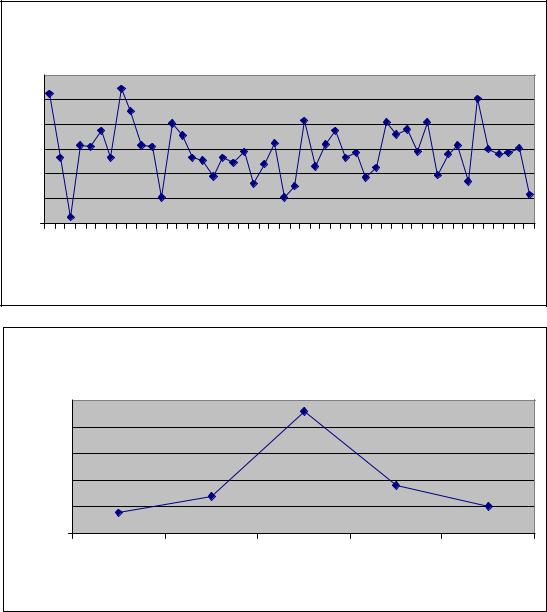
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
28 |
31 |
34 |
37 |
40 |
43 |
46 |
|
|
|
|
|
|
|
|
время |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частота |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1__6 |
|
6__11 |
11__16 |
|
16__21 |
|
21__26 |
||||||
|
|
|
|
|
|
интервал значенийуровнейряда |
|
|
|
|||||||
Рис.3. Временной ряд (флуктуации генерированы программой Excel) (а) |
|
|||||||||||||||
и его представление в виде кривой распределения (б) |
|
|
|
|
|
|||||||||||
Если величина С меньше нижней или больше верхней границы оценок табулированных для нормальных выборок (см. Приложение 3), то исследуемая последовательность наблюдений не имеет нормального распределения. Причем, в случае, когда превышается верхняя граница, это может указывать на наличие выбросов (сильно отклоняющихся значений отдельных наблюдений (см. разд.1). Если С находится в границах значений, приведенных в Приложения 3, то исходный ряд можно рассматривать как нормальный с принятым уровнем надежности.
30
При сопоставлении оценки С критерия с его табличными значениями особое внимание рекомендуется уделять границам, соответствующим уровню высокой надежности принятия гипотезы /6/. В этом же источнике приводится более полная таблица табулированных границ критерия.
Преобразования, нормализующие распределения Ряд задач (и, прежде всего, сравнения показателей отдельных ВР между собой,
анализ связей) обычно можно решать, оперируя только нормальными ВР. Следовательно, необходимо освоить методы их преобразование к нормальному виду. Очень часто для этого используется логарифмическое преобразование значений исходных наблюдений. Подобная трансформация уменьшает неоднородность дисперсий на отдельных отрезках ВР, снижает асимметрию распределения. Иногда даже полагают, что логарифмирование «полезно» всегда, так как оно отвечает «биологическим» особенностям изучаемых процессов морфометрического роста, увеличения численности популяций и т.п. /20, 21/. Однако, практика показывает, что если логарифмировать исходно нормальное распределение, то можно получить совсем не то, что ожидалось. В целом, с одной стороны, не следует ставить проведение преобразований в качестве самоцели. С другой стороны, если данные не имеют хотя бы приблизительно гауссовского распределения, то их обычно все же нужно привести к этому виду (или использовать методы непараметрической статистики). Возможные простые способы преобразования уровней ряда, которые могут позволить трансформировать его к нормальному распределению, приводятся нами в Приложении 4. Выбор в пользу применения той или иной формулы трансформации чаще всего решается эмпирически с учетом не только достигнутого соответствия нормальному распределению, но также исходя из соображений простоты вычислений.
Пример 6.
В течение опыта с лабораторной популяцией плодовой мушки дрозофилы из нее периодически брались выборки, в которых у самок исследовалась плодовитость /3/. Как следствие был получен хронологический ряд колебаний среднесуточной плодовитости мух, приводимый в табл. 2.5. Нам необходимо определить, характеризуется ли исходный ВР нормальным распределением и, если нет, то попытаться провести преобразования данных, которые обеспечат им распределение близкое к гауссовскому процессу.

31
Таблица 2.5 Хронологический ряд изменения плодовитости мух и его преобразования с целью
получения нормального распределения данных в ВР
№ п/п |
Плодовитость од- |
Преобразование ряда (в соответствии с |
|
|
ной самки/сутки |
рекомендациями Приложения 4): |
|
|
|
1/Хi |
|
|
|
ln Хi |
|
|
|
0,03086 |
|
1 |
32,4 |
3,48 |
|
2 |
25,5 |
0,03922 |
3,24 |
3 |
16,2 |
0,06173 |
2,79 |
4 |
39,9 |
0,02506 |
3,69 |
5 |
30,1 |
0,03322 |
3,40 |
6 |
32,1 |
0,03115 |
3,47 |
7 |
37,4 |
0,02674 |
3,62 |
8 |
21,1 |
0,04739 |
3,05 |
9 |
27,0 |
0,03704 |
3,30 |
10 |
58,7 |
0,01704 |
4,07 |
11 |
54,5 |
0,01835 |
4,00 |
12 |
39,7 |
0,02519 |
3,68 |
13 |
66,4 |
0,01506 |
4,20 |
14 |
69,1 |
0,01447 |
4,24 |
15 |
58,7 |
0,01704 |
4,07 |
16 |
67,8 |
0,01475 |
4,22 |
17 |
46,8 |
0,02137 |
3,85 |
18 |
61,9 |
0,01616 |
4,13 |
Размах (Р) |
52,9 |
-0,0473 |
1,45 |
Стандартное откло- |
17,22 |
0,01288 |
0,434 |
нение (σ ) |
|
3,67 |
|
С= | P/σ | |
3,07 |
3,34 |
|
Анализ табл.2.5 показывает, что исходный ряд по критерию отношения размаха изменчивости к его стандартному отклонению лишь «с малой надежностью» (в соответствии с Приложением 3) можно считать нормальным. Проведение рекомендуемого для временных рядов преобразования 1/Хi (Приложение 4) трансформирует исследуемую последовательность к нормальному распределению с «высокой надежностью» подобного вывода (Приложение 3). И, наконец, преобразование уровней исходного ряда путем логарифмирования (ln Хi,), хотя и делает распределение трансформированной последовательности более близким к гауссовскому процессу, однако в данном случае имеет меньшую эффективность, чем рассмотренное выше (1/Хi).
Следовательно, в случае необходимости дальнейшей статистической обработки ряда, характеризующего динамику изменения плодовитости самок дрозофилы, особен-
32
но при применении параметрических методов его анализа, желательно провести преобразования исходных наблюдений путем нахождения их обратных величин (1/Хi).
2.3. Анализ надежности построенных моделей Очень важным элементом анализа ВР является исследование остатков, получен-
ных после процедуры удаления тренда. Значение этого этапа определяется тем, что он позволяет оценить адекватность выбранной модели процесса исходным наблюдениям.
Возможны следующие ситуации.
1.Остатки случайны, нормально распределены, имеют нулевое среднее. Это означает, что цель достигнута - тренд удален. То есть, метод удаления тренда, например, подобранное аналитическое уравнение адекватно описывает исходные наблюдения. В дальнейшем подобное уравнение можно использовать в качестве модели процесса.
2.Значения остатков связаны (неслучайны). Следовательно, тренд не удален. Аналитическое уравнение процесса выбрано неудачно.
Таким образом, показатель независимости значений между уровнями остатков может быть мерилом для выбора того или иного аналитического уравнения тренда.
В качестве статистического приема оценки взаимной независимости уровней остатков обычно используют специальный критерий Дарбина-Уотсона /4, 18/.
Статистика критерия рассчитывается по формуле:
DW = |
∑(lt −lt −1 )2 |
≈ 2(1 −r ) |
(12), |
|
|
∑lt |
2 |
a |
|
|
|
|
||
где lt и |
lt −1 значения остатков, |
соответственно, в текущий и предшествующий |
||
моменты времени, ra – коэффициент автокорреляции первого порядка для ряда значений остатков.
Величина значений критерия DW может изменяться от 0 до 4. При полном отсутствии автокорреляции в остатках критерий Дарбина-Уотсона равен 2.
В Приложении 5 приведены нижняя (l1) и верхняя (l2) доверительные границы критерия Дарбина-Уотсона; k- число переменных в аналитическом уравнении процесса без учета свободного члена (см. разд.5); n - длина временного ряда.
Для применения критерия полученное значение DW сравнивают с его табличными границами (l1 и l2 ) при данном k. Если мы анализируем определенный хронологический ряд наблюдений или в случае парной регрессии, (см. разд. 5) k = 1.
33
При проведении процедуры расчета DW критерия возможны следующие варианты. 1. Если DW < 2, то полученное значение непосредственно сравнивается с табличными (по Приложению 5). 2. Если DW > 2, то находят разность: 4 - DW, и уже ее сравнивают с табличными значениями (см. Приложение 5). 3. Если DW < l1, то гипотеза о независимости остатков (H0) отвергается. Следовательно, аналитическое уравнение тренда плохо аппроксимирует исходные наблюдения (одной из причин этого может быть наличие осцилляций). 4. Если DW > l2, то гипотеза о независимости остатков (H0) принимается. Следовательно, тренд подобран удачно и возможно применение аналитического уравнения, описывающего его, для прогноза будущих значений ряда. 5. Если l1 ≤DW ≤l2, то для принятия определенного решения нет достаточных оснований. Вероятно, требуется продолжить наблюдения за исследуемым процессом.
Использование критерия при практических расчетах будет продемонстрировано далее (см. Пример 9 на с. 47).
34
34
3. Сравнение рядов
Нередко необходимо провести сравнение отдельных ВР друг с другом. При этом сравниваются обычно не сами ряды, а параметры, через которые они описаны. Приведем алгоритмы сравнения параметров двух ВР, имеющих нормальные (или хотя бы одинаковые) распределения.
Сравнение среднеарифметических рядов, характеризующих их центральную тенденцию, также как и сопоставление средних отдельных выборок, может проводиться по критерию Стьюдента. При этом можно использовать формулу (10).
Как указывалось выше, в некоторых задачах может возникнуть необходимость сравнить средние геометрические рядов. В этом случае необходимо прологарифмировать все наблюдения в анализируемых последовательностях, а затем найти простые средние арифметические трансформированных рядов и провести обычное их сравнение по t- критерию (10).
Сравнение дисперсий, характеризующих амплитуду ВР, производится по F – критерию Фишера:
(13),
где σ12 , σ22 - соответственно дисперсии для первого и второго ВР (причем за первую всегда берется большая из двух дисперсий).
Числа степеней свободы для сравнения полученного F критерия с его табличными (табулированными) значениями определяются как: df1 = n1 и df2 = n2, где n соответствующие значения количества наблюдений в сравниваемых рядах. Табличные значения критерия даны в Приложении 6.
Для сопоставления ВР по коэффициентам вариации специальной статистики нет, хотя мы и приводили возможную формулу оценки его ошибки (см. разд. 2.1.2).
Сравнения достоверности различий по периодам циклов между отдельными рядами обычно не производится. В некоторых задачах при вычислении нескольких значений периодов для отдельных циклов внутри каждого ВР или при рассмотрении нескольких оценок, объединяемых по разным ВР /12, 13/, длительность периодов можно охарактеризовать посредством простой средней арифметической, которую, в свою очередь можно, проанализировать посредством t- критерия Стьюдента (10).

35
Пример 7.
Рассмотрим, существуют ли различия по средней численности и размаху ее колебаний между двумя лабораторными популяциями дафний, содержавшихся при различном количестве корма (водоросль хлорелла).
Исходные данные о численности культур приведены в табл. 3.1. Проведенный анализ на нормальность исходных рядов показал, что они оба могут считаться имеющими гауссовское распределение (С=3,64 и С=3,23 соответственно для первой и второй популяции, которые сравниваются с табличными значениями по Приложению
3).
Если посмотреть на исходные данные, то между популяциями наблюдаются значительные различия, как в средней численности, так и в размахе ее колебаний. Популяция № 2, которая получала корма на порядок больше, чем № 1, имела более высокую среднюю численность. Оценка различий в средних численностях между популяциями по t – критерию (10) выявляет высокую их достоверность:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t = |
|
|
|
Υ1 − Υ2 |
|
|
1 = 221,6/(100,3*0.41)=5,4 |
||||||||
σ 2 (n −1) +σ 2 (n |
|
|
−1) |
* |
1 |
||||||||||
|
1 |
n |
+ n − 2 |
2 |
|
|
n |
+ n |
|
|
|||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
2 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
Табличное значение t для уровня значимости Р<0,001 и числу степеней свободы 22 (n1+n2-2) равно 3,79 (см. Приложение 2). То есть, так как 5,4 > 3,79, то средняя численность популяции № 2 достоверно (Р<0,001) выше средней численности популяции № 1.
Однако, выше указывалось (см. разд.2.1.2), что в случае достоверных различий в средних сопоставление амплитуд колебаний рядов по F критерию (13) является некорректным. Очевидно, необходимо попытаться преобразовать ряды так, чтобы исключить влияние средней на амплитуду циклов. С этой целью мы прологарифмировали данные обоих рядов.
Оценка нормальности логарифмированных рядов (табл.3.1) по С критерию (11) (С=3,55 и С=3,50 соответственно для первой и второй популяции) не выявила отклонений в их распределении от ожидаемого при гауссовском процессе. Анализ логарифмированных значений численности популяций (табл.3.1) позволяет сделать вывод, что наблюдавшиеся в исходных наблюдениях различия в амплитудах
36
колебаний целиком обусловлены влиянием средних значений. Так, если последний параметр и после преобразования уровней рядов достоверно выше во второй популяции по сравнению с первой (t=6,9, P<0,001 по Приложению 2), то различия в дисперсиях нивелируются (F = 2,32, P >0,05 по Приложению 6).
Итак, корректный анализ ВР выявляет отличия между ними только по средним, но не в дисперсиях. Отсюда, можно сделать минимум два вывода: 1. Чем больше получают особи корма, тем численность лабораторных культур дафний выше. 2. Однако амплитуда осцилляций численности рачков не зависит от характера их питания (во всяком случае в рассмотренном диапозоне варьирования фактора корма его действие на размах колебаний не установлено).
Таблица 3.1 Исходные численности двух лабораторных популяций дафний, содержавшихся
при различном кормовом режиме
Номер учета |
Численность |
Логарифм |
Численность |
Логарифм |
численности |
популяции №1 |
численности |
популяции № 2 |
численности |
|
|
популяции № 1 |
|
популяции № 2 |
|
|
|
|
|
1 |
71 |
4,26 |
55 |
4,01 |
|
|
|
|
|
2 |
63 |
4,14 |
136 |
4,91 |
|
|
|
|
|
3 |
54 |
3,99 |
402 |
6,00 |
|
|
|
|
|
4 |
50 |
3,91 |
505 |
6,22 |
|
|
|
|
|
5 |
48 |
3,87 |
464 |
6,14 |
|
|
|
|
|
6 |
48 |
3,87 |
247 |
5,51 |
|
|
|
|
|
7 |
122 |
4,80 |
135 |
4,91 |
|
|
|
|
|
8 |
85 |
4,44 |
263 |
5,57 |
|
|
|
|
|
9 |
40 |
3,69 |
410 |
6,02 |
|
|
|
|
|
10 |
30 |
3,40 |
270 |
5,60 |
|
|
|
|
|
11 |
28 |
3,33 |
247 |
5,51 |
|
|
|
|
|
12 |
63 |
4,14 |
227 |
5,42 |
|
|
|
|
|
Средняя |
58,5 |
4,0 |
280,1 |
5,5 |
|
|
|
|
|
Дисперсия |
666,27 |
0,17 |
19456,99 |
0,40 |
|
|
|
|
|
Коэффициент |
44,1 |
10,4 |
49,8 |
11,5 |
вариации (%) |
|
|
|
|
37
Отметим также, что если найти антилогарифм средней численности популяций, рассчитанный по данным в логарифмическом масштабе, то мы получим оценки средних геометрических исходных рядов (64,0 и 241,0 соответственно для первой и второй популяций), которые вычислялись ранее (разд.2.1.1) по более «громоздкой» формуле (3). Однако в программе Excel среднюю геометрическую найти еще проще, так как для этого существует специальная команда «СРГЕОМ» доступная в диалоговом окне «функция» ее основного меню.
