svetlosanov_v_a_osnovy_metodologii_modelirovaniya_prirodnykh

точки зрения локальный уровень представлен «точечной» моделью. Сельскохозяйственное поле представляет собой систему локального уровня. Леса, луга, прерии, саванны, пустыни и полупустыни в математических моделях могут быть представителями локального уровня природных систем.

Биологический компонент является очень чувствительным к возможным возмущениям компонентов экосистемы. Учитывая это обстоятельство, в дальнейшем будут рассмотрены математические модели численности популяций, где регуляторами динамического процесса являются рождаемость, смертность, миграция, конкуренция (внутренняя и внешняя) и т.д.

Региональный уровень моделирования включает большие по величине географические территории, объединяющие различные типы почв. Биотический компонент на региональном уровне достаточно разнообразен. Развитие во времени и пространстве любой административной области или района представляет антропогенную экосистему регионального уровня. Экономический компонент является ведущим в развитии антропогенных экосистем. В моделях регионального уровня экосистем учитывается: структура сообществ, внутривидовые соотношения, связь животных с растениями и микроорганизмами, межвидовые отношения, антропогенные воздействия.

Глобальный уровень включает моделирование динамики взаимодействующих антропогенных и природных экосистем в масштабах планеты. Рассматриваются возможности построения моделей сложных комплексных систем, описывающих социально - экономические, демографические, географические, климатические, и другие аспекты окружающей среды.

Существует большое количество работ по математическому моделированию всех трех уровней. Сделать анализ всех работ - весьма не простая задача. Но эта задача не является нашей целью. Наша цель - понять методологию математического моделирования природных систем, т.е. рассмотреть принципы создания математических моделей.

- 21 -

Для этого следует обратиться к математическим моделям, которые стали «классическими», проанализировать методику их построения, понять гипотезы, которые легли в основу их построения. Пропустив все идеи создания математических моделей через «свое сознание», можно будет перейти к созданию собственных моделей в области рационального природопользования.

Наибольшее внимание в последние десятилетия привлекают к себе глобальные динамические модели природных систем. Методология построения этих моделей будет в центре нашего внимания. Но прежде чем подойти к анализу глобальных моделей, надо осмыслить методику построения более простых моделей локального уровня, так как в основе построения глобальных моделей лежат те же идеи и гипотезы, которые сопровождают исследователя при создании моделей локального уровня.

Рассмотрение динамических моделей начнем с третьего класса как более простого по отношению к четвертому классу. При этом попытаемся разобраться в методике построения динамических математических моделей.

Выше указывалось, что любая экосистема включает в себя биотический (живой) компонент, который изменяется во времени и пространстве. Для понимания процесса функционирования динамических компонентов экосистемы в первую очередь целесообразно рассмотреть уравнения, характеризующие изменения численности особей.

Изменение во времени численности биотического компонента является общим свойством любой природной экосистемы. Поэтому, независимо от того, рассматриваются ли численности (или биомасса) животных или растений, бактерий или людей, желательно иметь теорию, описывающую хотя бы обобщенно изменение этой численности.

- 22 -

МЕТОДИКА ПОЛУЧЕНИЯ КОЛИЧЕСТВЕННЫХ ЗАВИСИМОСТЕЙ ИЗМЕНЕНИЯ БИОТИЧЕСКОГО КОМПОНЕНТА ЭКОСИСТЕМЫ ЛОКАЛЬНОГО УРОВНЯ.

Освоение методики построения математической модели локального уровня начнем с анализа развития во времени численности популяций.

Под популяцией обычно подразумевается совокупность особей одного вида, занимающую определенное пространство. Число особей представляет лишь один аспект в многообразии биотического материала. Тем не менее, эта величина служит важным ключом к пониманию поведения всех популяций в целом и представляет широкие возможности для исследований. Ни одно из исследований не может быть сколь – либо точным, если оно не начинается с построения достаточно приемлемой модели динамики рассматриваемой популяции. Здесь приходится идти на компромисс между крайностями: очень простую модель легко построить математически, но она слишком нереалистична, чтобы ей доверять. А с очень сложной моделью, которая ближе к действительности, очень трудно оперировать и анализировать полученные результаты моделирования.

Рассмотрим методику моделирования изменения численности популяции.

Существует лишь четыре основных фактора, которые воздействуют на численность популяций: рождаемость, смертность, иммиграция и эмиграция. Это утверждение может быть записано в следующей форме:

Здесь N t +1 - численность особей в момент времени t+1, N t - численность особей в момент времени t , В - число

родившихся особей за время t и t +1, D – число умерших, J - число иммигрировавших особей, Е - число эмигрировавших особей за тот же промежуток времени.

- 23 -

В определенных случаях такие факторы, как иммиграция и эмиграция могут быть незначительными (конечно, такие выводы можно сделать только в результате анализа реальной ситуации), и ими можно пренебречь. Для некоторых популяций вклад того или иного из указанных четырех факторов может быть равным нулю. Однако нет популяций, изменение численности которых определялось бы какими – либо другими факторами, кроме указанных четырех.

Ни один из членов уравнения (1.3) не является постоянным во времени, все они зависят от различных условий.

Вычитая N t из обеих частей уравнения, имеем:

Здесь b, d, i, e – коэффициенты, характеризующие рождаемость, смертность, иммиграцию и эмиграцию (средние величины на одну особь) в единицу времени. Предположим (для начала), что иммиграция и эмиграция незначительны. В результате получим следующее уравнение:

Предположим, что b,d - величины постоянные. Данное предположение ведет к созданию очень грубой модели, т.к. в реальности данное условие может выполняться только на коротком интервале времени. Для понимания ситуации постараемся осмыслить, что означают постоянные величины b и d. По своему физическому смыслу величины b и d означают усредненные по всем возрастам значения коэффициентов рождаемости и смертности популяции. Математически эти величины могут быть получены в результате следующих расчетов:

- 24 -

n1

∑bi N i

смертности тех же возрастных групп, n1 – предельный возраст рожениц, а n2 – возраст самой старой возрастной категории. В

реальности, коэффициенты bi , d i меняются во времени,

следовательно, меняются во времени и коэффициенты b и d. Но для начала (в целях построения упрощенной модели)

будем считать коэффициенты b и d постоянными. Для этого случая получим следующее выражение для изменения численности популяции (при t , стремящейся к нулю):

Решением уравнения (1.9) является экспонента. Известно, что экспонента – это кривая, которая

удваивает свое численное значение за определенный интервал времени. Но любая физическая величина не может расти по экспоненте на длительном промежутке времени. Предположим, что популяция начинает развиваться в среде с достаточным количеством пищи и при отсутствии хищников. В этом случае сначала ее численность растет очень быстро (близко к экспоненте). С течением времени запасы пищи истощаются, перенаселенность приводит к условиям менее благоприятным для выживания, плодовитость снижается и смертность увеличивается. Рост популяции часто идет по закону,

- 25 -

Проанализируем уравнение (1.11). Если α = 0 , то численность остается величиной постоянной, равной N 0 .

Рис. 1.4. Постоянная численность населения во времени

(α = 0 ).

Физически равенство величины α нулю означает, что рождаемость и смертность взаимно компенсируемы. При α f 0 (рождаемость больше смертности) численность популяция растет по экспоненциальному закону. Чем больше значение величины α , тем более круто идет вверх кривая.

Рис. 1.5 Экспоненциальный рост численности населения

(α f 0 ).

-27 -

При α p 0 (смертность больше рождаемости) численность популяции уменьшается по экспоненциальному закону (рис.1.6).

Рис. 1.6. Экспоненциальное падение численности населения

(α p 0 ).

Отметим, однако, что применение уравнения (1.9) в реальной действительности (при α f 0 ) ограничено, так как никакая величина, в том числе и численность популяции, не может расти бесконечно.

Т.е. рост численности популяции должен быть в реальных условиях ограничен какими - то физическими факторами. Решение этой проблемы математически предложил и осуществил Ферхюльст.

Ферхюльст рассматривал изменения численности популяции с учетом ее внутренних свойств и влияния окружающей среды. Учитывались самые разнообразные факторы: размножение, гибель, миграция, конкуренция и т.д. Так как природа роста очень сложна, естественно строить модель различной степени сложности. Сначала строится упрощенная модель, позволяющая определить численность организмов в популяции за различные моменты времени. После этого при необходимости может быть сформулирована более тонкая модель, описывающая физические, химические,

- 28 -

биологические процессы внутри организма, которые влияют на рост популяции.

Чтобы кривая не росла бурно вверх (до бесконечности), Ферхюльст предложил в математической модели наложить на экспоненциальный рост численности популяции некоторый фактор, который создает замедление и увеличивается с ростом численности популяции. Простейшее из возможных допущений состоит в том, что степень замедления роста для одного индивидуума пропорциональна размеру популяции, т.е., результирующая скорость роста для популяции равна не α , a величине, равной (α − β N ) , где β - коэффициент

замедления роста. Физически, это утверждение означает, что внутри системы (популяции) существует некий скрытый механизм (например, конкуренция за источники питания), который регулирует рост численности популяции.

Разность (α − β N ) можно также интерпретировать

следующим образом: скорость роста популяции является убывающей функцией ее численности. В этом случае уравнение изменения численности популяции записывается в следующем виде:

dt

При начальных условиях:

t = 0 , N = N 0

Уравнение (1.12) - это дифференциальное уравнение типа Бернулли, которое интегрируется в квадратурах. В результате интегрирования имеем:

N 0

Кривая (1.13), которая является решением уравнения (1.12), описывает изменение во времени численности популяции и носит название логистической кривой, наклон которой вначале возрастает, а затем постепенно уменьшается до нуля. Из формулы следует, что при очень больших

- 29 -

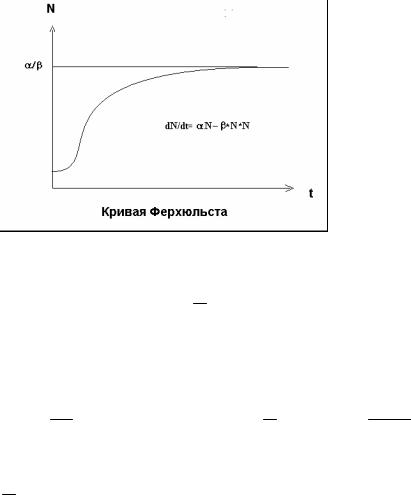
значениях времени численность популяции стремится к асимптоте, которая соответствует максимальной численности, способной находиться в данной среде.

Рис.1.7 Рост численности популяции с учетом внутренней конкуренции (кривая Ферхюльста).

Величина асимптоты α характеризуется отношением

β

скорости роста численности популяции α к коэффициенту замедления (внутренней конкуренции между особями популяции) β .

Уравнение можно представить также в другом виде:

dN = α N − β N 2 = α N (1 − β N ) = α N ( K − N ) dt α K

(1.14)

В этом случае в уравнение вводится параметр K, равный

α . Параметр K определяет асимптотическое равновесное

β

состояние популяции. Если в начальный момент времени популяция содержала число особей больше, чем K, то с течением времени численность особей будет уменьшаться и стремиться к значению K.

- 30 -