1avdin_v_v_matematicheskoe_modelirovanie_ekosistem

где µi – коэффициент смертности i-го компонента, µ′i – показатель скорости отмирания биомассы в зависимости от её концентрации Bi, m′i и m′′i – коэффициенты, отражающие заморные явления (задыхание гидробионтов от недостатка кислорода), t0*i – критический уровень температуры воды, при котором происходит изменение

характера зависимости смертности от температуры, θ > 1 – коэффициент, отражающий зависимость Mi от температуры. Для фитопланктона температурный оптимум в смысле минимума функции (43) колеблется от 18 до 22°С для различных районов рассматриваемой акватории.

Жизнедеятельность бактерий. Из экспериментальных исследований следует, что бактериопланктон (В1) играет важную роль в биологических процессах океана, участвуя в формировании пищевых ресурсов и обеспечивая замкнутость трофического графа за счёт потребления мёртвого вещества. Бактериопланктоном питаются фильтраторы, эвфаузииды и др. В агрегированном состоянии бактерии входят в пищевой рацион крупных копепод и хищного зоопланктона. Даже животныехвататели и личинки рыб могут употреблять агрегированный бактериопланктон, используя его как источник дополнительного питания. Так как не менее 30 % массы бактериопланктона находится в естественных агрегатах размером 3–5 мкм, то становится очевидной большая роль бактерий в образовании трофической структуры океанских экосистем.

Продукция бактерий в поверхностных слоях тропических олиготрофных районов сравнима с продукцией фитопланктона и может даже иногда превосходить её. Биомасса бактерий составляет 30–50 % от биомассы фитопланктона. На глубинах 400–500 м существует второй максимум бактериальной активности.

Бактерии, занимая особое положение в трофической пирамиде, отличаются изменчивым обменом, сильно понижающимся при недостатке пищи, что сопровождается соответствующим снижением скорости их роста. Пищей для бактерий в основном служит детрит (B10) и растворённое органическое вещество (РОВ, В13), выделяемое фитопланктоном. Поэтому рацион бактерий можно описать выражением:

R = min{ρ1,B1, k1,0B1[1 – exp(–k1,10B10 – k1,13B13)]},

где k1,0, k1,10, k1,13 – коэффициенты, определяемые экспериментально.

Обмен бактерий со средой описывается функцией Т1, отражающей величину энергетических затрат бактерий (с массой В1) в единицу времени:

Т1 = τ1B1[1 – exp(–k1,10B10 – k1,13B13)],

где τ1 – коэффициент пропорциональности.

Скорость отмирания бактерий опишем функцией

M1 = (µ1 + µ1′B1)B1,

где µ1 – мгновенная скорость отмирания бактерий при малой концентрации; µ1′ –

показатель усиливающего влияния роста биомассы В1 на смертность бактерий. Зоопланктон. Одним из основных промежуточных между фитопланктоном и

нектоном звеньев трофической пирамиды рассматриваемых экосистем является зоо-

51

планктон Bf, который, с одной стороны потребляет фито- и бактериопланктон, с другой – служит пищей многим промысловым животным. Поэтому зоопланктон представляет собой объект многочисленных исследований.

Величина рациона зоопланктона определяется по формуле Ивлева

где Df – биомасса доступной пищи, kf – максимальная величина относительного рациона при избытке пищи, νf – коэффициент, характеризующий скорость насыщения. Максимальный рацион принимается равным пищевым потребностям, которые, в свою очередь, определяются интенсивностью обмена Tf и максимально возможным

Формула (44) означает, что при малом количестве пищи Df рацион зоопланктона растёт пропорционально этой величине, затем по мере приближения рациона к максимальной величине kf он всё в меньшей степени зависит от Df.

Так как в реальных условиях, как правило, не происходит полного уничтожения одного трофического уровня другим, то в модели под Df понимается эффективная биомасса пищи, то есть вместо (44) корректней использовать формулу

где Vfmin – минимальная потребляемая концентрация пищи, а значение Vf – текущая потребляемая концентрация пищи, определяемая как Vf = k f 2 B2 + k f f.

Фактическая скорость изменения биомассы зоопланктона определяется также скоростью отмирания (коэффициент µf), затратами на энергетический обмен (коэффициент τf) и потреблением со стороны нектона (коэффициент Grf). На скорость изменения биомассы зоопланктона влияет также усвояемость пищи (коэффициент hf). Таким образом, для любого компонента зоопланктона, согласно формуле (42) справедлив следующий закон концентрации биомассы:

где Γf – множество подчинённости данного компонента зоопланктона, Hf = hfRf, Tf =

τfBf, Mf = µf(Bf)Bf, h f = 1− u−f 1.

Вуравнении (45) не отражены миграции компонентов зоопланктона. Обычно

визвестных моделях зоопланктон рассматривается как организмы, пассивно взвешенные в воде и не способные противостоять горизонтальным течениям, однако совершающие вертикальные суточные миграции. Например, амплитуда вертикальных миграций некоторых ракообразных может достигать сотен метров.

52

Самый простой способ имитации вертикальной миграции зоопланктона со-

стоит в том, что всю толщу воды мы делим на два слоя 0 – zf и zf – zmax и считаем, что часть зоопланктона из слоя zf – zmax с определённой периодичностью питается в слое

0 – zf. При этом происходит как потребление пищевых ресурсов в этом слое, так и перенос в него биогенных элементов из слоя zf – zmax.

Биогенные элементы. Биогенные элементы (В12) – P, N, Si и др. – играют существенную роль в процессе фотосинтеза фитопланктона и тем самым являются одним из звеньев экосистем океана, регулирующих в них поток энергии. Концентрации биогенов в морской воде колеблются в зависимости от района и глубины.

Биогенные элементы расходуются только в фотическом слое, определяя интенсивность развития фитопланктона. Будем предполагать, что потребление биогенных элементов пропорционально продукции фитопланктона с коэффициентом δ12. Пополнение запаса биогенных элементов в фотичесаком слое происходит за счёт их выноса при подъёме глубинных вод, где запасы биогенов считаются неограниченными, а также за счёт разложения детрита (с коэффициентом ρ10) и процесов метаболизма (с коэффициентом ρ1). Роль мигрирующих организмов в переносе биогенов из нижних слоёв в фотический слой, по сравнению с ролью гидродинамических процессов, незначительна.

Таким образом, изменение концентрации биогенных элементов во времени и по глубине можно описать уравнением

где ∆z – коэффициент турбулентной диффузии, β12 – коэффициент вертикальной адвекции.

Абиотические условия. Наиболее сложным моментом в построении модели является учёт влияния гидрологических и абиотических факторов на компоненты экосистемы и законы их изменения. Несмотря на большую неоднородность и разнообразие возможных сочетаний гидрологических и абиотических факторов по всему земному шару, всё же можно выделить основные закономерности. Известно, что температура воды в океане является невозрастающей функцией глубины, причём вертикальное распределение температуры существенно зависит от расположения термоклина. Из-за этого распределение температуры по глубине можно аппроксимировать двухступенчатой функцией

t°(z) = T01 при0 ≤ z ≤ zT ,

T02 при zT < z ≤ zmax .

Термическая структура океана является одним из существенных факторов, и поэтому в модели для верхнего гомогенного слоя 0 – zT величина Т01 изменяется регионально. Для глубин z > zT температура воды постоянна и равна Т02. В свою очередь, Т01 является функцией температуры атмосферы и зависит от адвективного переноса воды. В пределах тропической зоны годовая амплитуда средней месячной

53

температуры на поверхности океана составляет всего 2–6°С, что позволяет считать в этой зоне Т01 не зависящей от пространственных координат.

Положение термоклина, подстилающего верхний слой и препятствующего дальнейшему проникновению тепла на глубину, в тропической зоне изменяется от zT = 10 м до zT = 150 м. В целом по земному шару определение положения термоклина можно дать, например, исходя из предположения о структуре глобальной циркуляции океанской воды. Можно считать, что глубина термоклина зависит только от расстояния до экватора, причём термоклин симметричен относительно экватора. От экватора он заглубляется, достигая наибольшей глубины в средних широтах, и вблизи 50–60° с. ш. и ю. ш. он поднимается он поднимается к поверхности. В экваториальной зоне можно принять zT = 40–100 м.

Учёт физических процессов переноса вещества за счёт турбулентной диф-

фузии и течений. Океанская среда характеризуется большой физической изменчивостью, учёт которой в уравнениях модели существенен для решения вопроса её идентификации. Предположим, что имеется водная среда с каким-либо компонентом В. Символ В представляет концентрацию компонента в произвольной точке водной среды. Это может быть концентрация детрита или биогенных элементов. Пусть рассматриваемый объём воды перемещается со скоростью v, проекции которой на оси координат равны vx, vy и vz. Тогда изменение B(t, x, y, z) во времени и пространстве можно описать уравнением сохранения массы

которое в значительной степени определяет структуру пятнистости акватории и где ∆x, ∆y – горизонтальные составляющие коэффициента турбулентной диффузии, ∆z – его вертикальная составляющая. В среднем эти величины для океана оцениваются значениями 0,26–0,5 см2/с. При изотропности вихревой диффузии в горизонтальной плоскости ∆x = ∆y = νН. Масштабность диффузии всегда определяется временным

Учёт в модели турбулентной диффузии связан с рядом больших трудностей, вызванных малой изученностью этого вопроса и необходимостью согласования масштабов диффузии с шагом дискретизации пространства. Турбулентную диффузию моделируют на основе предположения, что она аналогична молекулярной диффузии, то есть описывают выражениями, стоящими в правой части уравнения (46). Согласно Г. Одуму, коэффициент турбулентной диффузии должен возрастать с увеличением масштаба рассматриваемого явления, принимая значения от 102 до 106 см2/с при изменении масштаба длины от 100 м до 10 км. При этом от поверхностного слоя воды до глубины в несколько десятков метров диффузия уменьшается на порядок.

Для целей моделирования достаточно рассмотреть приближённое описание, в рамках которого движение океанской воды можно рассматривать как иерархию турбулентных вихрей различных масштабов длины и времени. При этом непрерывный распад больших вихрей на более мелкие обеспечивает передачу энергии к самым малым вихрям (< 10–2 м), где она диссипируется силами вязкости и переходит в тепло. В рассматриваемых моделях горизонтальные масштабы значительно превышают

54

этот минимальный уровень и составляют величины в десятки и сотни километров. Поэтому учитываемая турбулентность генерируется внешними планетарными причинами, так что для описания турбулентных вихрей можно использовать теорию ло- кально-изотропной турбулентности Колмогорова [22], согласно которой энергия е распределяется по различным масштабам " движений в соответствии с законом е(" ) ~ ε2/3"5/3, где ε – скорость передачи энергии по нисходящему каскаду вихрей. При этом характерные для размера " величины – скорость v" и масштаб времени τ" можно оценить величинами v" ~ ε–1/3"1/3 и τ" ~ ε1/3"2/3. Отсюда, согласно теории Колмогорова и в соответствии с исследованиями Р.В. Озмидова коэффициент νН можно оценить с помощью характерного времени τ и характерной длины " по формуле νН ~ ε1/3"4/3 ~ ετ 2. Например, для Северного моря при " ~ 5 км имеем νН ~ 102 м2/с.

εв различных условиях может изменяться на 5 порядков от 10–10 до 10–5 м2/с.

Вчастности, в зависимости от глубины изучаемого слоя океана значения ε в среднем

можно оценить величинами: ε = 3 10–6…3 10–5 выше термоклина, 3 10–8…3 10–7 в термоклине, 3 10–10…3 10–9 ниже термоклина.

Нектон. Будем считать, что вводимый нами компонент нектон буквально означает совокупность океанских животных, отличающихся крупными размерами, способных к активному самостоятельному передвижению независимо от течений и имеющих промысловое значение. При этом будем пренебрегать планктонной стадией развития нектона, считая такой подход в глобальном масштабе незначительным. Нектонные организма могут потреблять растительную и животную пищу, среди них имеет место каннибализм. Они могут совершать вертикальные и горизонтальные миграции. Рацион нектона описывается формулой Rr = min{ρrr, Rrr}, где Rrr = krrHrФHrz, HrФ = 1 – exp(–Vr), Vr = krФB2 − krf Bf − krr r, Hrz = exp(–drzθФrz). ρr – максимальный коэффициент отношения продуктивности к биомассе (П/Б), krФ и krf – коэффициенты, определяющие содержание фитопланктона и планктона в пищевом рационе нектона, krr – показатель каннибализма, drz – показатель степени лимитирования роста некто-

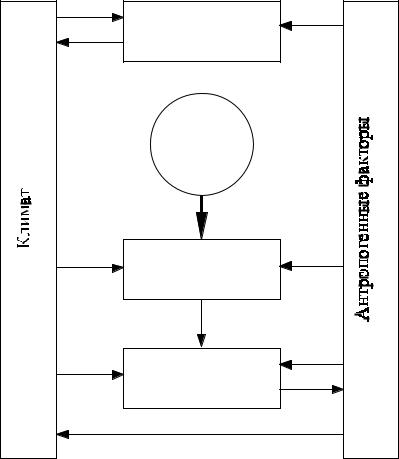
Глобальная модель функционирования океанической биоты. Как показано в исследованиях, модель функционирования всей экосистемы Мирового океана может быть создана путём суперпозиции региональных моделей. В качестве блока модели биосферы примем блок-схему, изображённую на рис. 13. Сплошные линии – потоки энергии (вещества), штриховые – информационные связи. В этом случае во-первых Мировой океан описывается точечной моделью, во-вторых, согласно данным исследований, приемлемой для целей моделирования учёт двух биотических уровней: фитопланктона и нектона. Запишем уравнения моделей.

55

Атмосфера

Энергия

солнечной

радиации

Е

Фитопланктон

Ф

Нектон r

мальный П/Б-коэффициент фитопланктона, год–1, kФ – показатель интенсивности фотосинтеза, bФ – параметр, отражающий лимитирование скорости фотосинтеза недостатком или избытком биомассы фитопланктона, αФТ – коэффициент, указывающий, на сколько процентов изменится скорость фотосинтеза при отклонении глобальной температуры от начального значения на 1°С, Е* – оптимальный для фотосинтеза уровень освещённости, аФС – показатель скорости фотосинтеза как функции концентрации углерода, dФ – показатель лимитирования фотосинтеза загрязнениями океана, τФ – затраты на энергетический обмен единицы биомассы фитопланктона, год–1, µФ

и µ′Ф – показатели скорости отмирания фитопланктона, θi – доля загрязнений i-го ре-

56

гиона, сбрасываемых в океан, kGФi – весовой коэффициент, отражающий долю фитопланктона в пищевом рационе населения i-го региона.

Для нектона, r, т/км2:

i=1

показатель продуктивности нектона, αrT – коэффициент, указывающий, на сколько процентов изменится продукция нектона при отклонении глобальной температуры от её начального значения на 1°С, krФ – показатель степени лимитирования продукции нектона концентрацией фитопланктона, drz и µrz – показатели зависимости от загрязнений океана соответственно продукции нектона и его смертности, µФ и µ′Ф –

показатели зависимости скорости отмирания нектона от его биомассы, hr и τr – коэффициенты, отражающие затраты (на единицу биомассы нектона) на неусвоенную пищу и энергетический обмен со средой, λGri – характеристика промысловых усилий при добычи нектона i-м регионом, ωr – коэффициент, отражающий форму зависимости интенсивности дыхания от веса тела.

Таким образом, мы получили сводку тех фактов, которые характерны для процессов функционирования океанической биоты и описания из математически. Рассмотренный вариант блока модели является первым приближением, рассматривающем трофическую и пространственную структуры экосистем Мирового океана.

12. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ НАЗЕМНЫХ ЭКОСИСТЕМ

Основной частью моделей наземных экосистем является блок продукционного процесса растений. Результаты моделирования имеют как теоретическое значение, так и практическое значение. Первое заключается в возможности понять и связать в единое целое знания о продукционном процессе; второе – в прогнозировании урожая некоторых агрокультур. Мы рассмотрим модели годичной продукции растений, опирающееся на установление зависимости годичной продукции от климатических факторов.

Продукционный процесс наземных растений можно представить состоящим из четырёх фундаментальных процессов: фотосинтеза, отмирания, дыхания и роста. В основе продукционного процесса лежит фотосинтез, уравнение которого можно записать в следующем виде:

СО2 + Н2О + световая энергия → СН2О + О2.

В процессе фотосинтеза растения под воздействием солнечной энергии поглощают из атмосферы СО2 и корневой системой из почвы воду и биогенные элементы и создают органическое вещество в виде ассимилятов. Одновременно происходит транспирация, которая обеспечивает снабжение растений водой, питательны-

57

ми элементами и регулирует тепловой режим растений. Скорость фотосинтеза зависит от интенсивности фотосинтетически активной радиации (ФАР) – участка солнечного спектра 380–710 нм, водного и температурного режимов, концентрации СО2 в атмосфере, плодородия почвы и видовых особенностей.

Пусть плотность биомассы растительности на суше описывается переменной Р (т/км2). Изменение Р в глобальном масштабе аппроксимируем обыкновенным дифференциальным уравнением

где ρP – максимальный П/Б-коэффициент (отношение продуктивности к биомассе) рассматриваемого типа наземной растительности, RPP – продуктивность растительности при меньших чем ρP текущих значениях П/Б-коэффициента, MP и TP – величины отмирания и затрат на дыхание в единицу времени.

Рассмотрим уравнение (47). Продукция растительности описывается зависимостью, мультипликативно отражающей роль различных факторов окружающей среды:

где kPC и bP – коэффициенты функции, учитывающей зависимость продукционного процесса от биомассы растительности, kPО – показатель влияния концентрации кислорода в атмосфере на продуктивность растительности, функции НРЕ, НРС, НРZ, НРW и НРТ учитывают воздействие соответственно энергии солнечной радиации, углекислого газа, загрязнённости среды, влажности почвы и температуры на динамику роста растительности.

Зависимость интенсивности фотосинтеза НРЕ от освещённости можно выразить формулой, аналогичной формуле (48) в предыдущей теме, если считать, что для наземных растений фотосинтез лимитируется недостатком или избытком освещённости:

где ЕП – интенсивность ФАР, E*P – оптимальная освещённость.

Рассмотрим математическое выражение процессов, протекающих в отдельном растении. Главный процесс – это фотосинтез. Монси и Саеки (M. Monsi, T. Saeki) [23] предложили следующую формулу для вычисления интенсивности фотосинтеза листа растения:

где k – максимальное значение фотосинтеза, а – начальный наклон кривой фотосинтеза листа. Согласно (49) интенсивность фотосинтеза увеличивается с ростом освещённости, достигая насыщения при больших значениях ЕП.

58

Углекислый газ определяет питание растений из атмосферы и при современной его концентрации ограничивает фотосинтез. Зависимость фотосинтеза от освещённости и концентрации СО2 в атмосфере можно выразить формулой Шартье

(P. Chartier) [24]:

где С1 – концентрация СО2 в атмосфере, а1 и а2 – коэффициенты, определяемые из экспериментов. Согласно формуле (50) при постоянной освещённости интенсивность фотосинтеза увеличивается с ростом концентрации атмосферного СО2, достигая насыщения при достаточно высокой его значении. При постоянных концентрациях СО2 интенсивность фотосинтеза увеличивается с ростом освещённости; при современной концентрации СО2 в атмосфере интенсивность фотосинтеза линейно зависит от концентрации СО2.

При постоянной освещённости, согласно (50), имеем:

где CP – концентрация СО2 в атмосфере, при которой достигается значение функции

(51), равное аР/2.

Следующий важный фактор, регулирующий фотосинтез – тепло. Максимальная интенсивность фотосинтеза достигается при некоторой оптимальной температуре, уменьшаясь при её увеличении и уменьшении. Зависимость интенсивности фото-

где Т – температура воздуха, Tmax – значение температуры, при которой интенсивность фотосинтеза максимальна, Р0 – интенсивность фотосинтеза при Tmax, αРТ – коэффициент пропорциональности.

Важное значение для фотосинтеза имеет обеспеченность водой, поступающей в растения через корневую систему. Вода не только непосредственно участвует в химической реакции фотосинтеза, но и регулирует физические условия протекания этой реакции.

Одна из форм саморегулирования у растений – транспирация – испарение воды с поверхности листьев. Интенсивность транспирации во много раз превышает испарение в отсутствии фотосинтеза. Транспирация предотвращает перегрев листа за счёт тепла, выделяющегося при фотосинтезе. На образование 1 г органического вещества используется 0,6 г воды и около 500 г воды при этом испаряется за счёт траспирации. Функциональное отражение зависимости интенсивности фотосинтеза от концентрации воды в почве выглядит следующим образом:

ФL = 1 – exp[–kPW(WS + WSG)],

где WS – величина поверхностного стока, WSG – количество воды, вносимое искусственно за счёт орошения, k – коэффициент влажности почвы.

59

Кислород ингибирует процессы фотосинтеза. Зависимость фотосинтеза от концентрации О2 в атмосфере описывается следующем соотношением:

фотосинтеза в оптимальных условиях, k′PO – интенсивность фотосинтеза в фазе на-

сыщения. При концентрациях кислорода меньших, чем O*P , зависимость линейна.

Кроме углерода, водорода и кислорода для построения органического вещества наибольшее значение среди химических элементов имеют азот, калий и фосфор. Они поступают в растение через корневую систему в виде усвояемых соединений. Азот может также непосредственно фиксироваться из воздуха. Зависимость интенсивности фотосинтеза от содержания питательных элементов хорошо выражает принцип лимитирующих факторов Либиха: синтез ограничивает только одно из питательных веществ – находящееся в минимуме. В реальных условиях увеличение концентрации любого из веществ в некоторых пределах увеличивает фотосинтез, уменьшение – снижает. Зависимость фотосинтеза от совместного влияния питательных веществ можно выразить формулой

ФL = A1[1− exp(− m1C1)][1− exp(− m2 Z2 )][1− exp(− m3Z3 )][1− exp(− m4 Z4 )],

где A1 и mi (i = 1, 2, 3, 4) – коэффициенты, С1 – концентрация СО2 в атмосфере, Z2, Z3, Z4 – концентрации в почве питательных форм азота, фосфора и калия.

Как установлено в эксперименте, увеличение концентрации любого из биогенных элементов выше некоторого порогового значения приводит к снижению интенсивности фотосинтеза.

Второй фундаментальный процесс – дыхание растений. Если фотосинтез идёт только в листьях, то дыхание – результат процессов, протекающих во всех частях растения: в листьях, стволе, корнях. Дыхание обеспечивает снабжение энергией различных биохимических процессов синтеза, связанных с ростом растения, построением новых структурных элементов (дыхание роста). Кроме того, дыхание обеспечивает поддержание живых структур органов растений (дыхание существования). При этом затрачивается органическое вещество, накопленное в органах растений. Интенсивность дыхания ТР можно представить в виде ТР = (τ1 + τ2(Т))Р, где τ1 – коэффициент, а τ2(Т) – функция, возрастающая с ростом температуры воздуха Т.

Чистая продукция органического вещества – нетто-фотосинтез – Ф есть разность между приростом органического вещества в результате фотосинтеза (бруттофотосинтез) и его расходом при дыхании: Ф = ФL – TP. То есть чистый прирост биомассы обеспечивается превышением фотосинтеза над дыханием. При достаточно высокой температуре фотосинтез и дыхание сравниваются. Максимум чистой продукции достигается при меньшей температуре, чем максимум фотосинтеза.

60