8.4. Скорость, ускорение и энергия колеблющегося тела.

Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного процесса.

Пусть имеем тело массы «m», которое совершает под действием квазиупругой силы колебания по закону:

, тогда

.

.

Видно, что скорость и ускорение также изменяются по гармоническому закону (графики приводились ранее) с периодом колебаний равным T. Из сравнения формул видно, что скорости v опережает смещение по фазе на . Это означает, что если x=0, то v тела имеет максимальное значение .

Для ускорения зависимость иная. В каждый момент времени ускорение пропорционально смещению и находится с ним в противофазе. Это означает, что когда x=x_max, то ускорение тоже максимально, но отрицательно, т.е. при x=x_max, (графики приведены ранее).

Квазиупругая сила, под действием которой происходит колебательное движение, является консервативной. Поэтому полная энергия гармонического колебательного движения должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно (силами сопротивления пренебрегаем). Причем в моменты наибольшего отклонения о положения равновесия , причем ; при прохождении положения равновесия , причем . Так как , то .

Определим, как со временем изменяется Е_к и U_п для гармонического колебания . Имеем

(8.4)

(8.5)

Т.к. , то имеем

,

т.е. как и должно было быть, т.к. квазиупругая сила – консервативная сила.

Используя формулы тригонометрии, можно получить выражения для

Рис. 8.5

(8.6)

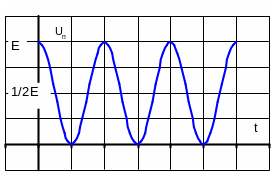
(8.7)

Здесь E – полная энергия системы. Из формул видно, что Е_к и U_п изменяются с частотой 2₀, т.е. с частотой вдвое превышающей частоту гармонического колебания. Среднее значение квадрата sin и квадрата cos равно 1/2. Следовательно, среднее значение E_к совпадает со средним значением U_п и равно E/2.

ЛЕКЦИЯ 11

8.5. Гармонический осциллятор.

Систему, описываемую уравнением , где , будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:

.

Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия.

Для гармонического осциллятора справедливы все результаты, полученные ранее для гармонического колебания.

Рассмотрим и обсудим ещё дополнительно к ним два вопроса.

Найдем импульс гармонического осциллятора. Продифференцируем выражение по t и, умножив полученный результат на массу осциллятора, получим:

. (8.8)

В каждом положении, характеризуемом отклонением “x”, осциллятор имеет некоторое значение ”p”. Чтобы найти ”p” как функцию ”x”, нужно исключить ”t” из написанных для ”p” и ”x” уравнений, Представим эти уравнения в виде:

(8.9)

Возведя эти выражения в квадрат и складывая, получим:

. (8.10)

Н

Рис. 8.6

арисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·₀”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].

Найдем теперь площадь эллипса . Или

.

Здесь , где ₀ – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.

Следовательно, . Откуда

. (8.11)

Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора.