МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Донской Государственный Технический Университет ДГТУ А.Н.Зубков, М.Н.Павлова Матрицы и их применение Учебное пособие Ростов-на-Дону 2011

1

§ 1. Матрицы и операции над ними

Матрицей называется прямоугольная таблица чисел вида

,

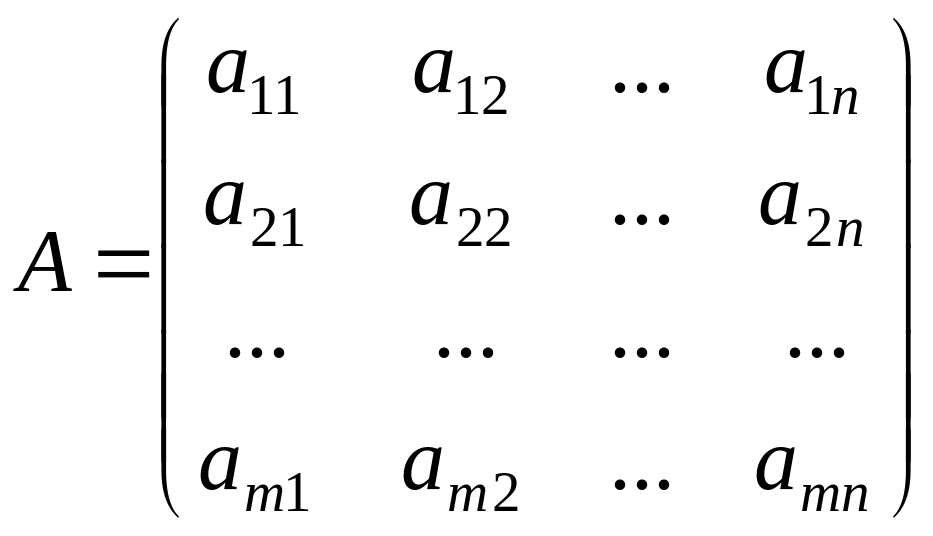имеющая n столбцов и m строк. Числа a_ij, ; , называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут . Иногда матрицу обозначают в виде

= (a_ij ).

Если , то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если при любых

:

.

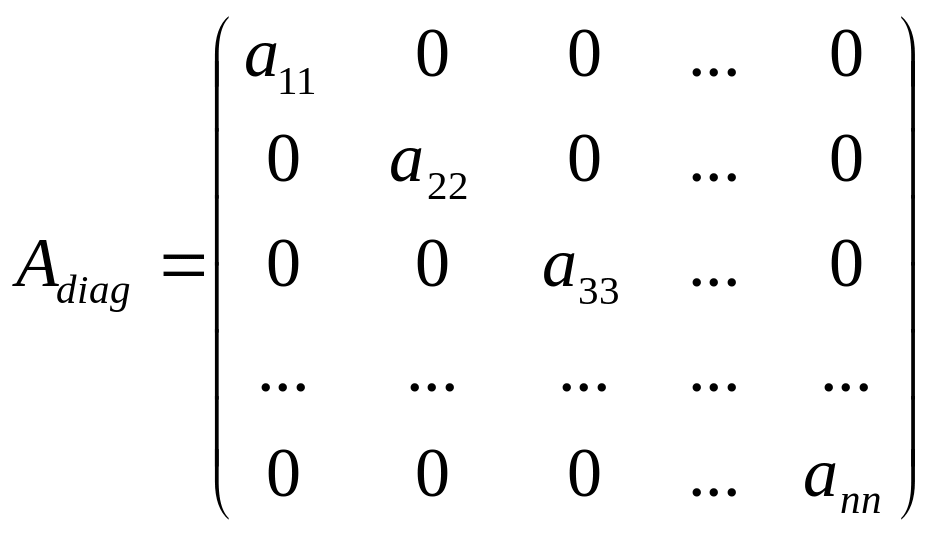Диагональная матрица, у которой все элементы главной диагонали , , называется единичной и обозначается буквой Е:

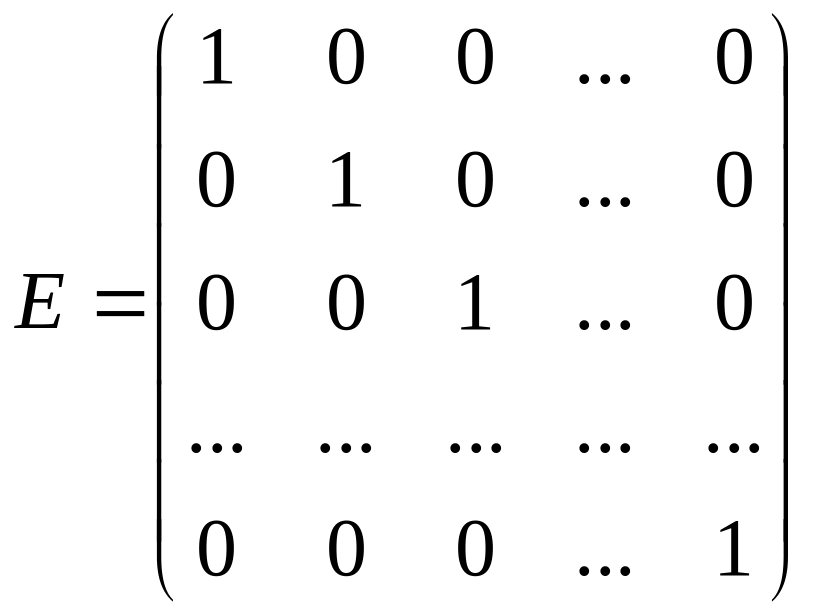
Матрица вида

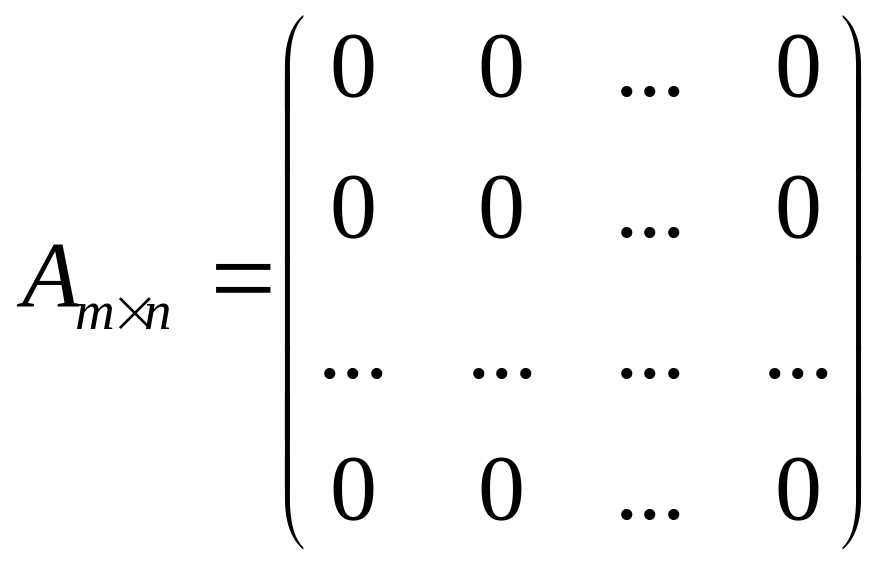
2

называется нулевой и обозначается О.

Квадратная матрица называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица называется вектором-строкой, а матрица 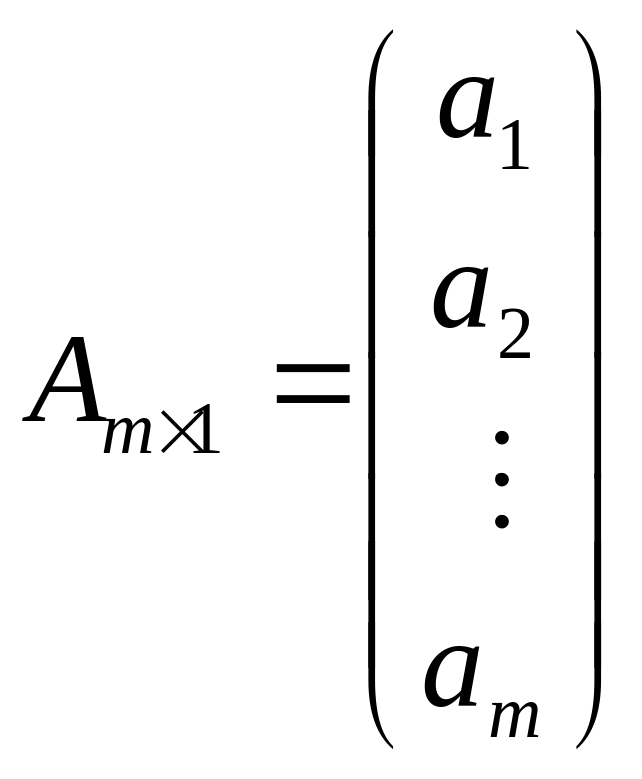называется вектором-столбцом, - одноэлементная матрица.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается . например, если , то , а если , то . Матрица называется симметрической, и обозначается А, если . Для такой матрицы .

Определение. Матрицы , равны между собой, , если , ; .

Произведением матрицы на число  называется матрица , для которой c .

Пример. , .

Суммой двух матриц и называется матрица , для которой .

Пример. .

Аналогично определяется разность матриц.

Операции сложения матриц и умножения матрицы на число являются линейными операциями, так как обладают следующими свойствами:

1. ;

2.

3.A+O=A;

4. ;

5. ;

6. ;

7. ;

8. ;

9. .

Упражнение. Доказать, что .

Над матрицами можно производить элементарные преобразования:

1. перестановка местами двух строк или столбцов;

2. умножение всех элементов строки или столбца на число ;

3. прибавление ко всем элементам одной строки или столбца соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Д ве матрицы и - эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут АВ. При помощи элементарных преобразований матрицу можно привести к элементарному каноническому виду В, т.е. к матрице, у которой существуют , , а , . Например:

   

    

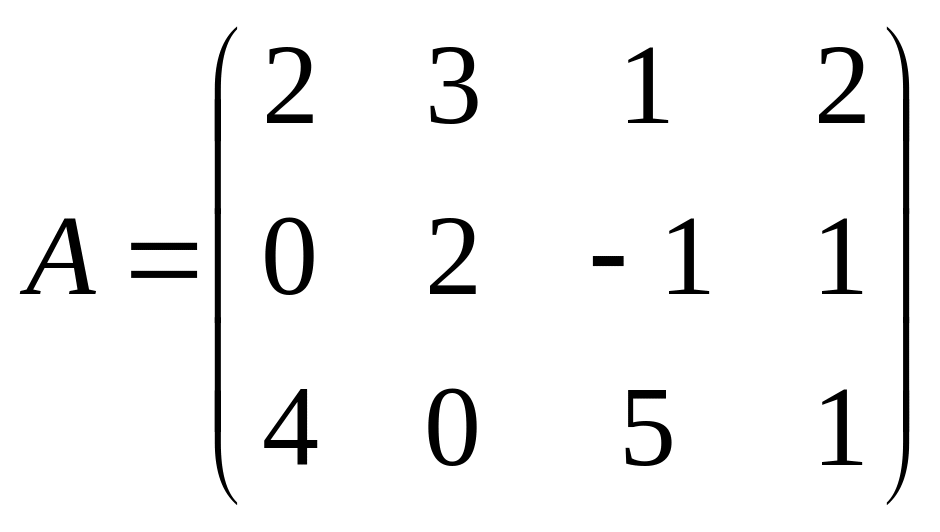
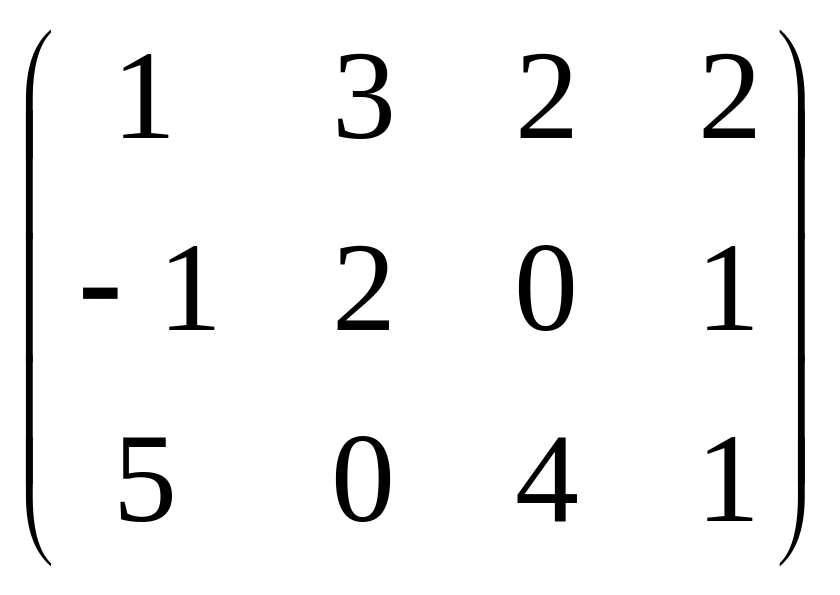
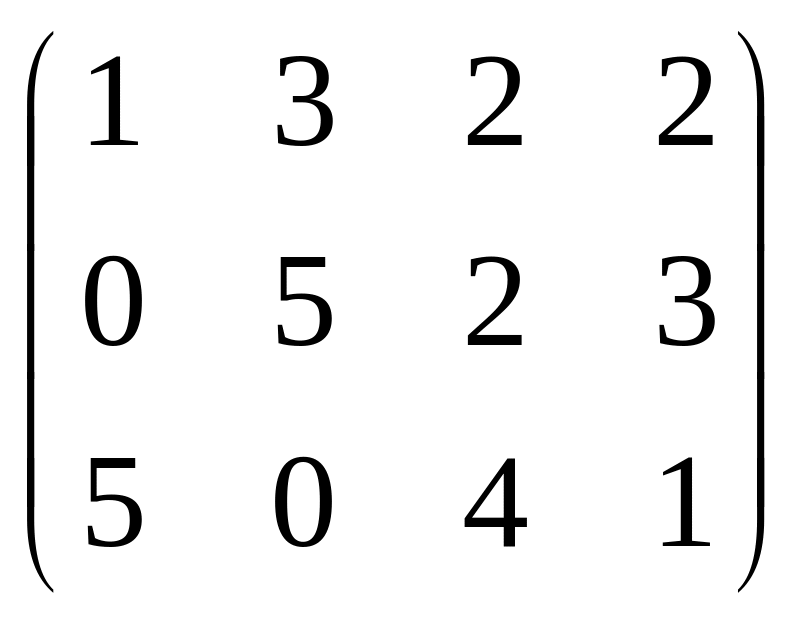
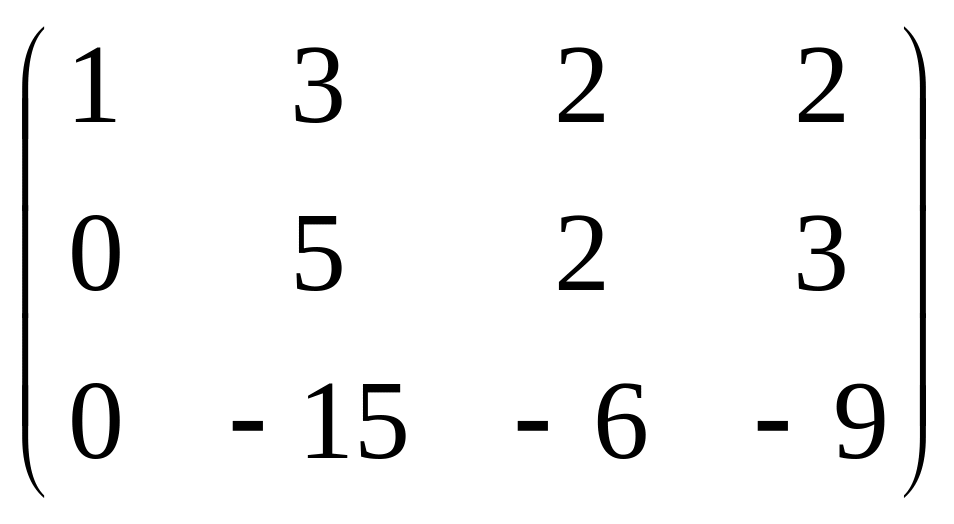
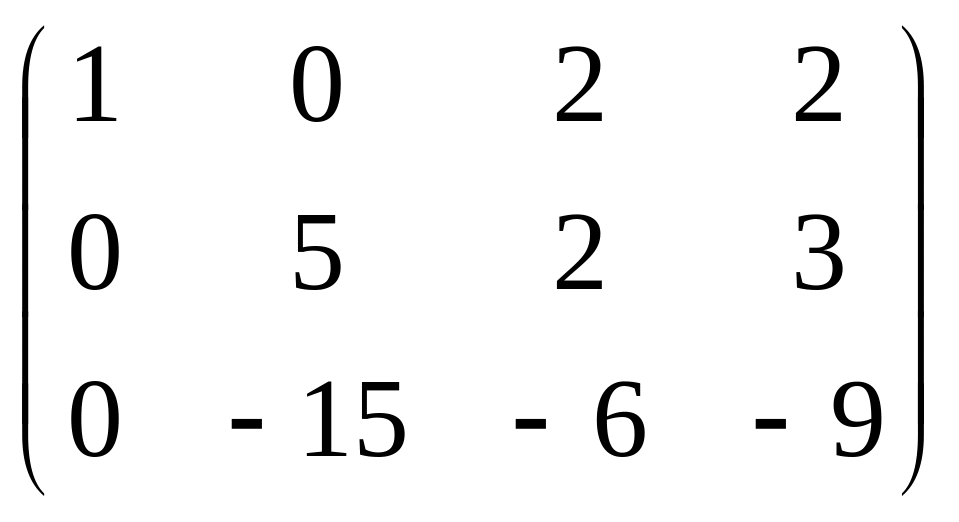
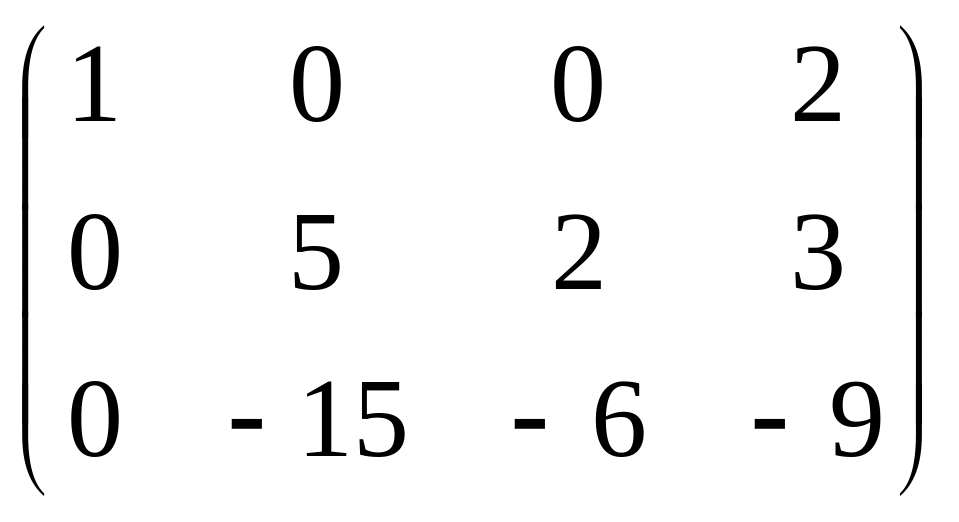
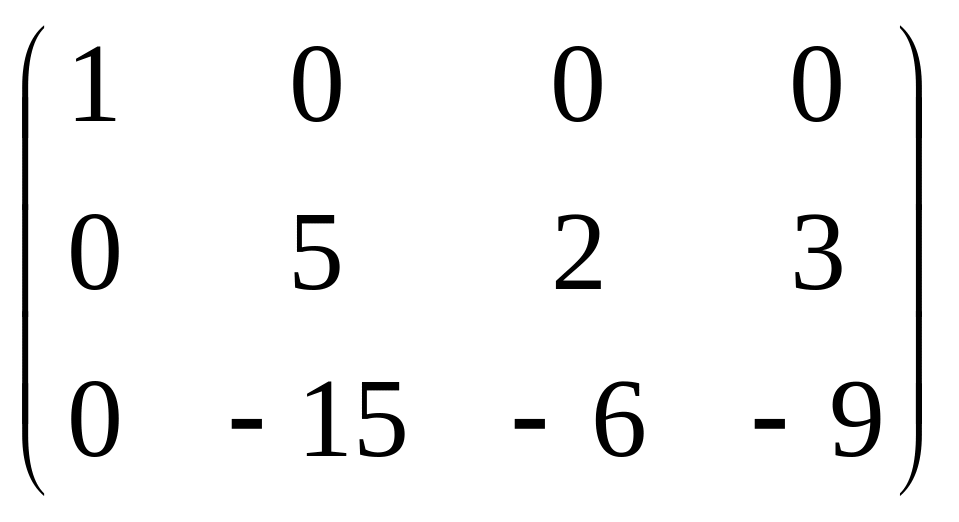
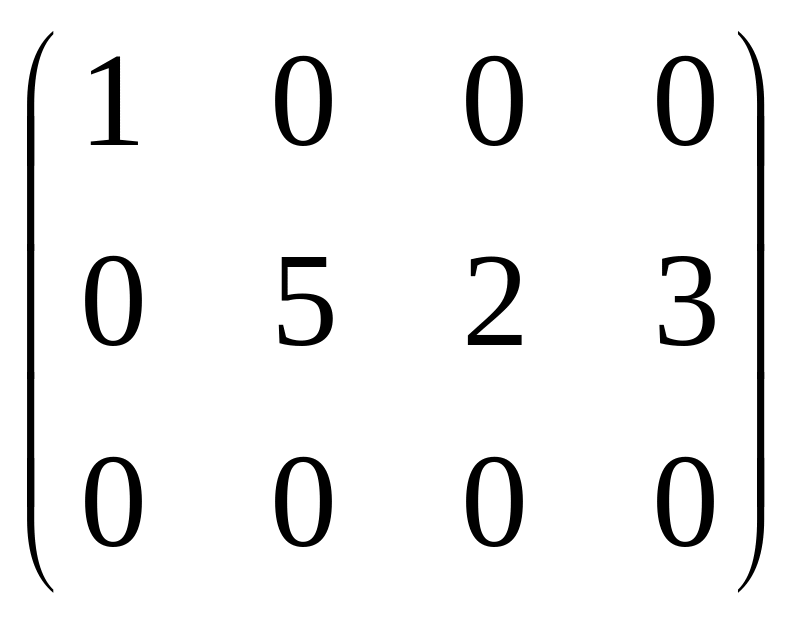
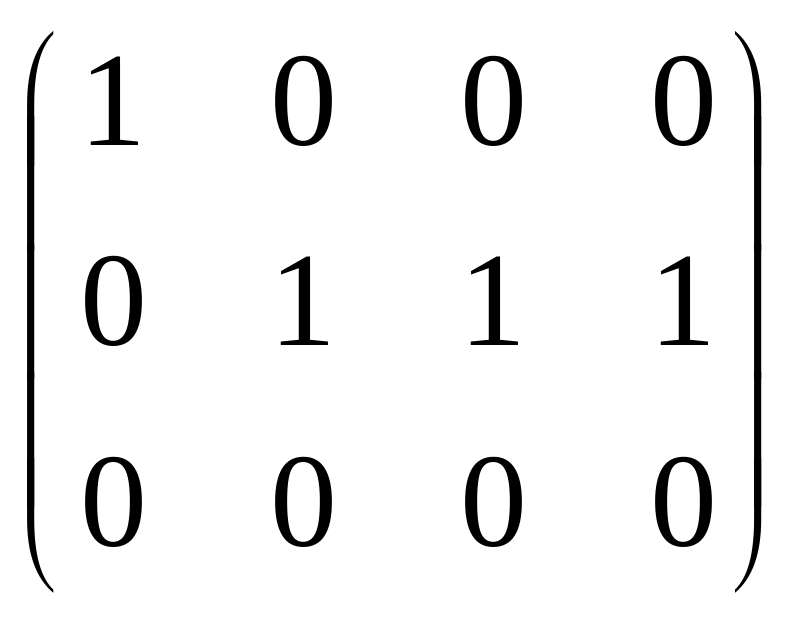
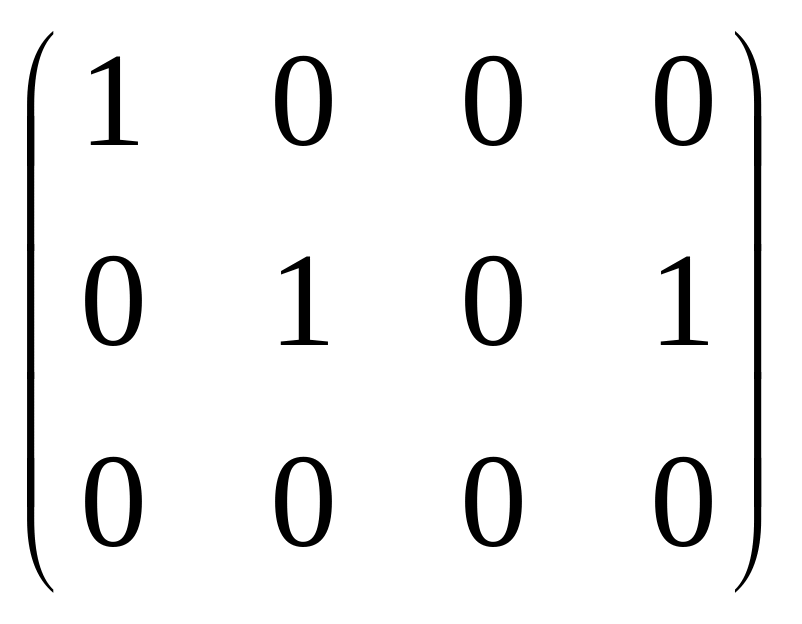
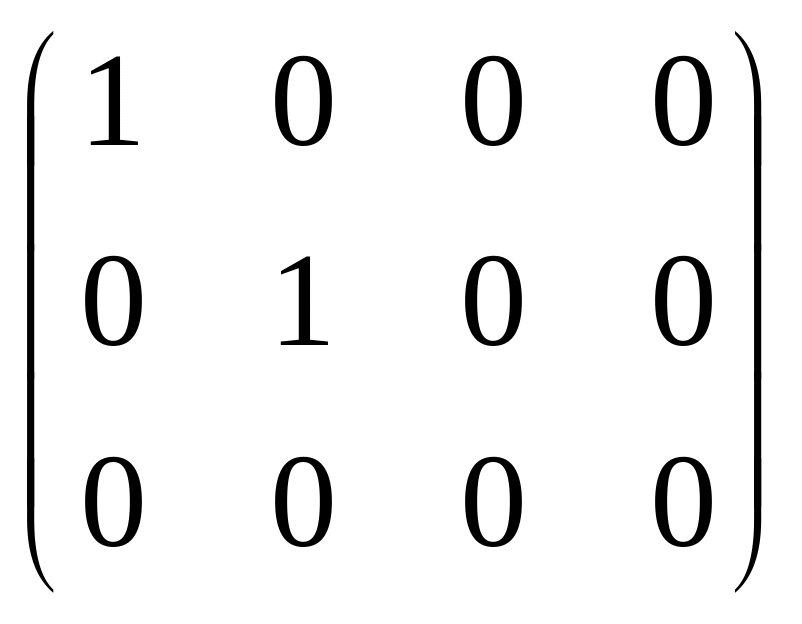   =B.

Если число столбцов матрицы равно числу строк матрицы , то определяется произведение этих матриц , при котором получается матрица такая, что

(поэлементное умножение i-ой строки матрицы А на k-й столбец матрицы В).

Пример. Пусть и .

Тогда

Однако здесь произведение не существует, так как , где 3 - число столбцов для матрицы В, а 2 - число строк для А.

Если и , то существуют матрицы и , при этом . В общем случае . Например, если , , то .

Умножение матриц обладает следующими свойствами:

1. ;

2. ;

3. ;

4. .

§ 2. Определитель матрицы и обратная матрица

Каждой матрице можно сопоставить число det A , |A| или , которое называют определителем матрицы и находят следующим образом:

1. . ;

2. .

;

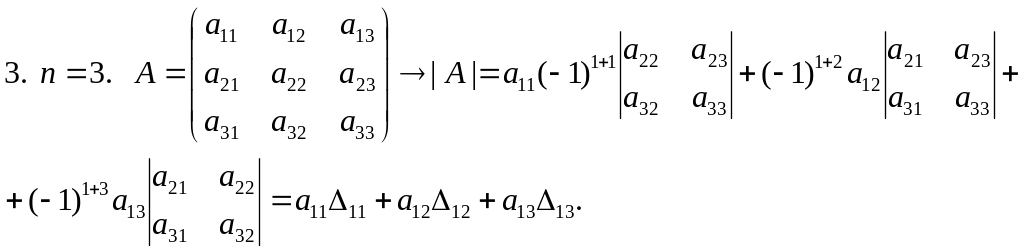
4. В общем случае, если A = , то det A находится с помощью разложения Лапласа: , , где A_ij= - алгебраическое дополнение элемента , т.е.

_ij = ,

где - минор элемента , т.е. определитель квадратной матрицы А, полученный из А вычеркиванием i-ой строки и j-ого столбца.

Пример.

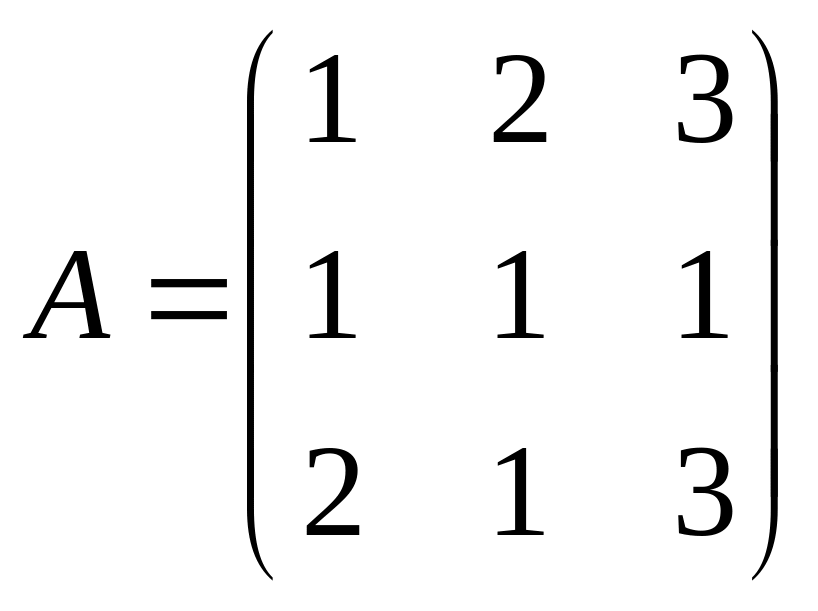
Можно показать, что (использовать правило Лапласа) и что  если имеются в А нулевая строка или нулевой столбец или две пропорциональные строки или столбца.

Наибольший из порядков миноров матрицы A_nn называется еерангом и обозначается r, или rang A. Очевидно, что . Минор, порядок которого определяет ранг матрицы, называется базисным. Ранг матрицы А равен числу единиц на главной диагонали канонической матрицы, к которой приводится матрица А путем элементарных преобразований. Например,

.

Квадратная матрица A=.A_nn называется невырожденной, если , т.е. базисный минор совпадает с определителем матрицы . В противном случае, когда rangАn, A называется вырожденной матрицей. В этом случае .

Матрица B= , удовлетворяющая условиям

,

называется обратной к A_nn и обозначается . Таким образом,

.

Если A - невырожденная матрица, то существует обратная к ней матрица

,

где матрица =(_ji) называется присоединенной матрицей к , i,j=1,2,…, п.

Пример. Дана матрица . Найти обратную к ней матрицу А^-1.

Вычислим вначале определитель этой матрицы. Имеем .

Находим затем алгебраические дополнения A_ij элементов матрицы A.

Получим , , ; .Следовательно, матрица из алгебраических дополнений имеет вид .Находим транспонированную к ней матрицу .Таким образом, .

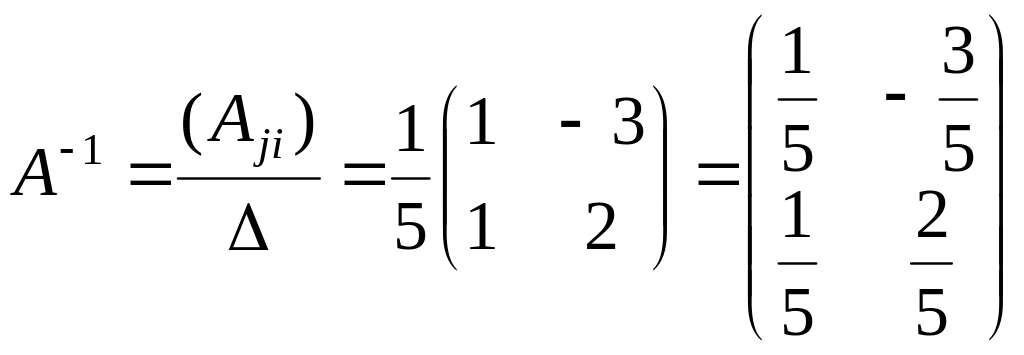Проверка: .

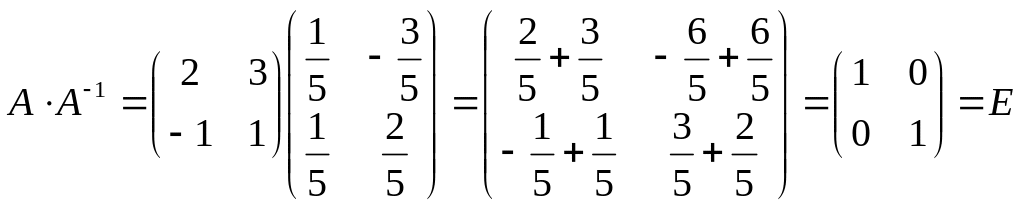Замечание. Если , то матрица называется ортогональной.