Атомный фактор.

В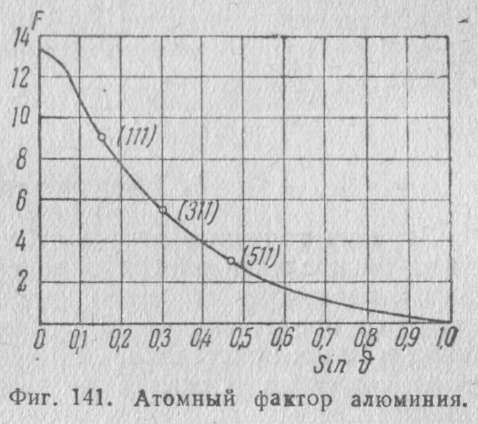 первоначальном нашем выводе мы предполагали, что весь заряд каждого атома сосредоточен в математической точке — узле пространственной решетки. При таком условии лучи, рас­сеянные в любом направлении всеми Z электронами одного и того же атома, совпадают по фазе и при взаимодействии ампли­туды их суммируются, так что амплитуда излучения, рассеянного атомом в любом направлении, в Z раз больше амплитуды излу­чения, рассеянного единичным электроном (Z — число электро­нов, вращающихся вокруг ядра атома). Однако мы знаем, что в действительности электроны, вращающиеся вокруг ядра, рас­сеяны по всему объему атома. Расстояния между электронами, принадлежащими одному и тому же атому, являются величи­нами, соизмеримыми с длиной волны рентгеновых лучей. Поэтому лучи, рассеянные разными электронами одного и того же атома, могут отличаться друг от друга по фазе и, следовательно, их амплитуды нужно складывать геометрически, с учетом разно­стей фаз.

Абсолютная величина (модуль) геометрической суммы векто­ров всегда меньше арифметической суммы модулей этих векто­ров, поэтому при сложении Z колебаний, имеющих амплитуды, равные А_{электрона} равнодействующая амплитуда А_атома должна по­ручить меньше, чем Z А_{электрона}. Квадрат отношения (А_атома/ А_{электрона})²=F² носит название атомно­го фактора. Последний зави­сит от:

- количества электро­нов Z;

- от их распределения в атоме;

- угла брэгговского отражения θ.

Очевидно, ин­тенсивность рассеянных лу­чей пропорциональна вели­чине атомного фактора.

Значения атомного фактора любого химического эле­мента являются, как учит тео­рия и подтверждает опыт, функцией отношения sinθ/λ причем с увеличением этого отношения величина атомного фактора непрерывно падает. Кривые, изображающие зависимость F=f(sinθ/λ) называются F-кривыми. Их можно строить либо на основании экспериментальных данных, либо на основании вычислений.

На рис. 141 изображена полученная экспериментально F-кривая при рассеянии алюминием (а —4,04 А) лучей К_α-молибдена (λ=0,708 А). При θ=0 атомный фактор максимален, он равен числу электронов в атоме (в данном случае Z =13). При отражении от плоскости (111) F— 8,7, для (311) F = 5, а для (511) F=2,7. Интенсивность лучей пропорциональна квадрату атомного фактора, следовательно, несовпадение фаз лучей, рассеянных разными электронами одного и того же атома, в данном случае приводит к ослаблению интенсивности отражения от плоскости (311) по сравнению с отражением от (111) в три раза, а лучи, отраженные от (511), ослаблены по сравнению с (111) в десять раз.

Поэтому во всех тех случаях, когда нужно сравнивать между собой интенсивности интерференционных максимумов, индексы которых сильно отличаются друг от друга, необходимо учиты­вать атомный фактор.

Вводя атомный фактор, мы должны преобразовать структур­ный множитель так:

Общее выражение для интенсивности лучей, для кристаллов, построенных из атомов только одного химического элемента, примет вид: