2. Обратная решетка.

 

Понятие обратной решетки играет важную роль в дифракции электронов как в объеме твердого тела, так и на его поверхности. Условия дифракции легко интерпретируются на основе законов сохранения энергии и импульса с добавлением вектора обратной решетки.

Для трехмерного случая, если a,b и c– базисные векторы трансляции прямой решетки, то соответствующие векторы обратной решетки a*,b* и c* определяются следующими векторными соотношениями:

 

              .                           (4.5)

 

            Смешанное произведение, стоящее в знаменателях соотношений (4.5) равно, как известно, объему прямой решетки.

            Любой вектор обратной решетки записывается через элементарные векторы обратной решетки:

 

                                                                                  (4.6)

 

где h, k, l – любой набор целых чисел (индексы Миллера).

            Вектор обратной решетки (4.6) обладает следующими свойствами:

-         он перпендикулярен семейству плоскостей прямой решетки с индексами Миллера hkl;

-         его длина обратно пропорциональна расстоянию между этими плоскостями.

            Общее правило построения обратной решетки можно распространить и для двумерного случая. Для этого необходимо формально заменить вектор трансляции с на единичный вектор n в направлении, перпендикулярном поверхности.

 

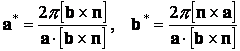                                .                                   (4.7,а)

 

Поскольку величина численно равна площади параллелограмма со сторонами a и b и углом между ними α, то абсолютные значения a* и b* векторов двумерной обратной решетки можно представить в виде [5]:

 

                          ,                                               (4.7,б)

 

причем .

           

На рис. (4.5) приведен пример построения обратной решетки. Прямая решетка, определяемая элементарными векторами трансляции a и b и обратная решетка с элементарными векторами a^* и b^* располагаются в плоскости рисунка. Узлы прямой решетки показаны светлыми кружками, обратной – темными. Для прямой решетки приведены в качестве примера две линии (штриховые прямые) из семейства атомных рядов (11) и (21). Индексы Миллера h=1, k=1 и h=2, k=1 соответственно для семейства рядов (11) и (21) определяют величину отрезков, отсекаемых этими рядами на координатных осях. Векторы обратной решетки g₁₁ и g₂₁, также показанные на рисунке, перпендикулярны соответствующему семейству рядов двумерной прямой решетки.

   Следует заметить, что в отличие от трехмерных кристаллических структур, симметрии поверхностных прямых и обратных решеток совпадают [6].

    Следует особо подчеркнуть, что в отличие от трехмерного случая, когда обратная решетка представляет собой точки в обратном пространстве, обратная решетка плоского кристалла представляет собой совокупность прямых линий (стержней обратной решетки), которые расположены перпендикулярно плоскости кристалла (и плоскости обратной решетки). Эти стержни располагаются в обратном пространстве периодически с векторами трансляции a^* и b^*. На рис. 4.5. стержни обратной решетки располагаются перпендикулярно плоскости рисунка и пересекают плоскость обратной решетки в точках, обозначенных темными кружками.

            Этот результат можно получить, если формально устремить период прямой решетки в направлении, перпендикулярном плоскости кристалла (направление, параллельное вектору прямой трехмерной решетки с) к бесконечности при переходе от трехмерной к двумерной структуре [5]. Тогда период обратной решетки в направлении вектора обратной решетки с^* будет стремиться к нулю. По этой причине ряд узлов обратной решетки в направлении вектора с превратиться в прямые линии. Эта особенность геометрического представления обратной решетки становится существенной при интерпретации результатов по дифракции электронов на двумерных структурах.

 Лекция 2.12. Сфера Эвальда. Дифракция в терминах обратной ре­шетки.