
- •Кратні і криволінійні інтеграли
- •§1 Подвійний інтеграл
- •Поняття подвійного інтеграла.
- •§2. Геометричні застосуваання.
- •§3. Застосування подвійного інтеграла у фізиці.
- •§4 Потрійний інтеграл.
- •2.Геометричні та фізичні застосування потрійного інтегралу
- •§5 Криволінійні інтеграли.
- •Криволінійний інтеграл I роду.
- •Приклад:
- •Приклад 2
- •Формула Гріна (зв‘язок з подвійним інтегралом)
§5 Криволінійні інтеграли.
Криволінійний інтеграл I роду.
Нехай існує плоска
крива рівняння , якої![]()
![]() - диф.
дуги, якщо
- диф.
дуги, якщо
![]() ,
то
,
то
![]() >0,
та
>0,
та
![]() ,
якщо
,
якщо
![]() ,
то
<0
та
,
то
<0
та
![]()
![]() .
.
Якщо - функція, неперервна на кривій К, то під її криволінійним інтегралом I роду, взятим по кривій К розуміють інтеграл
(1)
![]()
Якщо К завдана
рівнянням
![]() ,
маємо
,
маємо
![]()
Нехай К- матеріальна,
тобто має масу і![]() -
якась дуга кривої К, якій належить т.М,
а
-
якась дуга кривої К, якій належить т.М,
а
![]() -
маса цієї дуги. Тоді частка
-
маса цієї дуги. Тоді частка![]() -
середня густина дуги
-
середня густина дуги
![]()
![]()
![]() т.б. границя
середньої густини дуги за умовою, що
дуга
т.б. границя
середньої густини дуги за умовою, що
дуга
![]() в
т.М, її називають лінійною густиною дуги
в т.М
в
т.М, її називають лінійною густиною дуги
в т.М
![]() -
маса нескінченно малої дуги
-
маса нескінченно малої дуги
![]() таким чином.
таким чином.
О зн.1
(Фізичний зміст інтегралу I
роду)
зн.1
(Фізичний зміст інтегралу I
роду)
![]() - маса лінії
- маса лінії
Властивості
1. При зміні
напрямку інтегрування криволінійного
інтегралу I
роду не змінює свого значення

Якщо крива інтегрування
 ,
то
,
то


Про середнє
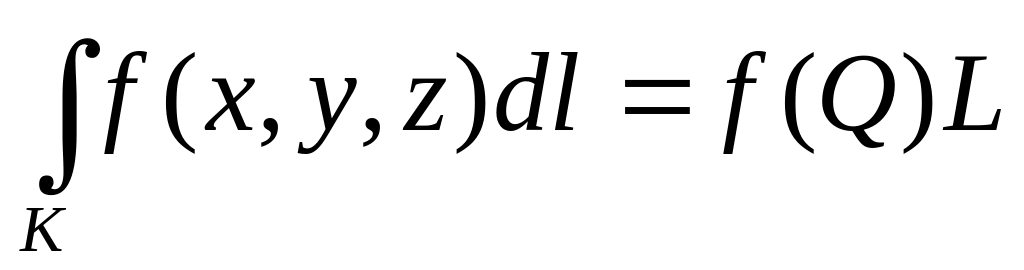 , де
, де
 L
– довжина
L
– довжина
Приклад:
Знайти масу півкола
![]() ,
якщо лінійна густина в т.М пропорційна
ординаті Y.
,
якщо лінійна густина в т.М пропорційна
ординаті Y.
![]()
Рішення: t
– полярний кут,
![]() - параметри рівнянння кола
- параметри рівнянння кола
1
 M(X,Y)
M(X,Y)

 t
t
0 1
![]()
![]() ,
,
к - коефіцієнт пропорційності.
![]()
![]()

![]() =2к
=2к
Приклад 2
![]()
Рішення :
![]()
![]() =
=![]()
2.Криволінійний інтеграл II роду.
Нехай
![]() - гладка, або кусково-гладка функція
та
- гладка, або кусково-гладка функція
та
![]() - пара функцій
неперервних на кривій К. Так як
- пара функцій
неперервних на кривій К. Так як
![]()
О значення
2 Під
криволінійним інтегралом II
роду від 2-х функцій Х та
значення
2 Під
криволінійним інтегралом II
роду від 2-х функцій Х та
У, взятими по кривій К розуміють інтеграл
![]() (2)
(2)
Якщо шлях К
завдається рівнянням
![]() ,
то (2) приймає вигляд:
,
то (2) приймає вигляд:
![]()
Аналогічно, якщо
![]() ,
то
,
то
![]()
Властивості
1) При зміні шляху інтеграл (2) міняє знак
![]()
2) Якщо
,
то
![]()
Приклад ![]() вздовж :
вздовж :
1) прямої ОА
2) от А – парабола С вершина О та ОУ
3) ОВА – ламана.
4) ОСА – ламана.


 C2
A(1;2)
C2
A(1;2)


0 1B
Рішення 1)
Рівняння ОА :
![]()
![]()
2)Рівняння параболи:
![]() ,
знайдемо к
,
знайдемо к![]()
![]()
3)
![]()
ОВ
![]()
ВА
![]()
![]()
4)
![]()
3.Фізичний зміст криволінійного інтегралу II роду.
Нехай
![]() змінна
сила, яка неперервно змінюється та
змінна
сила, яка неперервно змінюється та
 - шлях К , пройдений
точкою прикладення, де
- шлях К , пройдений
точкою прикладення, де
 Y K
Y K
F
Ds

M(X,Y) M(x+dx;y+dy)
0 X
так як нескінченно
малому шляху
неперервну силу
![]() можна вважати постійною, то елементарна
робота сили дорівнює
можна вважати постійною, то елементарна
робота сили дорівнює
![]() (3) , інтегруючи
його по К отримаємо
(3) , інтегруючи
його по К отримаємо
![]()
О зн.3
зн.3
Криволінійний інтеграл II роду є робота змінної сили вздовж шляху інтегрування, проекціями якої на координатні осі являються відповідні коефіцієнти при змінних диференціалах.
Приклад : Знайти
А змін.
![]() ,
точки прикладення якої описується
параболою ОВ
,
точки прикладення якої описується
параболою ОВ
![]()
4 M2


M1 F2


F1
0 2
![]()
4.Умови незалежності криволінійного інтегралу II роду
від шляху інтегрування.
Нехай АВ - К –
напрямлена крива в просторі з початком
А і кінцем В, тоді усі дотичні до АВ
також являються напрямленими прямими.
Нехай кути, які утворюють дотичні до
АВ з вісями координат
![]()
![]() …
Вони є ф-ні координати
…
Вони є ф-ні координати
![]() точки дотику М.
Візьмемо на АВ елементарну дугу
точки дотику М.
Візьмемо на АВ елементарну дугу
![]() і будемо вважати її прямолінійною .
Тобто
- вектор з проекціями
і будемо вважати її прямолінійною .
Тобто
- вектор з проекціями
![]() напрямлений, так як крива АВ
напрямлений, так як крива АВ
![]()
![]()
Тоді
![]() - формула зв’язку
I
та II
роду.
- формула зв’язку
I
та II
роду.
О зн.4 Вважається, що інтеграл не залежить від форми кривої, якщо інтеграл вздовж будь-якої кривої, що з‘єднується цими точками має одне і теж саме значення.
![]()
M

B
N
A
0
Теорема Для того, щоб криволінійний інтеграл не залежав від форми кривої необхідно і достатньо щоб виконувалось співвідношення
![]()
Обчислювання цього інтегралу спрощується, якщо за шлях інтегрування взяти ламану, ланки якої паралельні координатним вісям.
Приклад Обчислити

![]()
2 B(2;2)

1


0 1 2

![]()
5.Криволінійний інтеграл увздовж замкненого контуру.
Замкнений контур маємо, коли початок і кінець кривої співпадають.
Для визначення напрямку інтегралу задається додатковий напрям проти руху годинникової стрілки.


 B
B


A
У випадку просторового контуру додатний напрям задається, коли при русі поверхня залишається зліва.
Позначається такий
інтеграл
![]()
