3.2 Характеристики рівняння другого порядку

Означення. Рівняння (3.6), (3.7) називається характеристичним для рівняння (3.1), а його інтеграли характеристиками .

Рівняння (3.7) розпадається на два рівняння

. (3.8)

Позначимо – дискримінант рівняння (3.8). Знак підкореневого виразу визначає тип рівняння (3.1).

Рівняння називається рівнянням гіперболічного типу, якщо у точці ; еліптичного, якщо ; параболічного, якщо . У різних точках області визначення рівняння може бути різних типів.

Надалі будемо вважати, що коефіцієнти рівняння (3.1) є неперервними функціями разом з частинними похідними до 2-го порядку включно у розглядуваній області та не перетворюються одночасно в нуль. Тоді, якщо рівняння (3.6) можна розкласти на лінійні множники та подати у вигляді

або, якщо

Кожне із наведених рівнянь розпадається на два

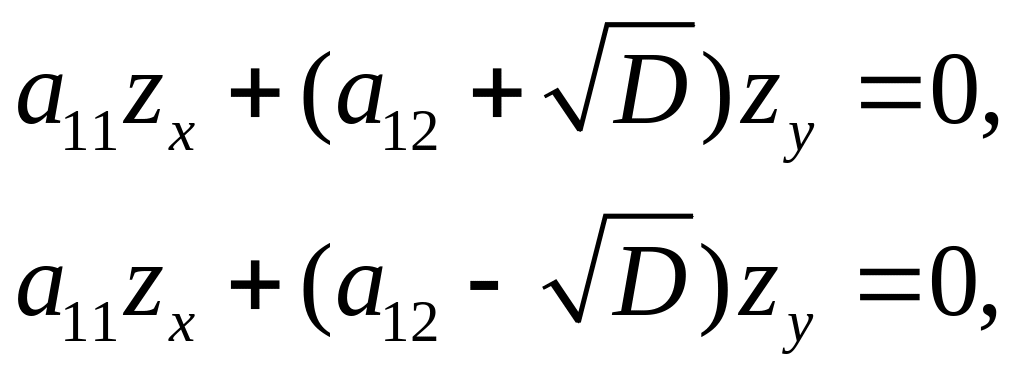(3.9)

або

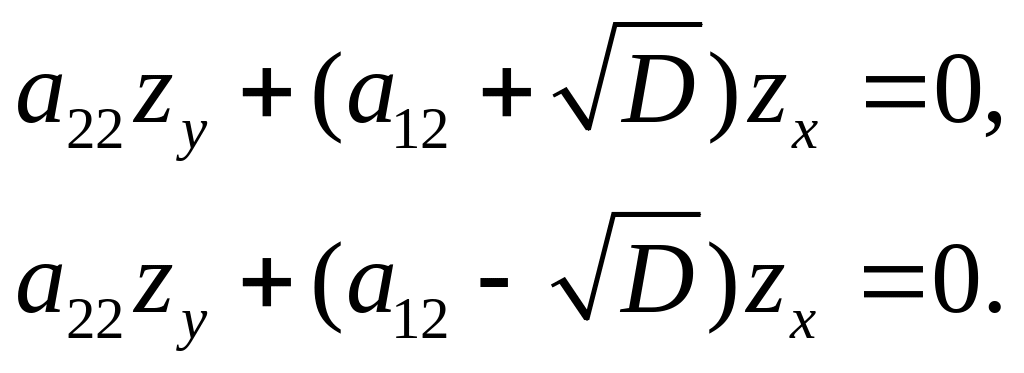(3.10)

Отже, розв’язки кожного із рівнянь (3.9) або (3.10) будуть розв’язками рівняння (3.6).

Для їх інтегрування складаємо відповідну їм систему звичайних диференціальних рівнянь

,

або (3.11)

звідки одержуємо рівняння пари характеристик для рівняння (3.1)

або (3.12)

Із курсу звичайних диференціальних рівнянь відомо, що якщо функція є загальним інтегралом одного із диференціальних рівнянь (3.11) або (3.12) (тобто деяким загальним інтегралом рівняння (3.7)), то функція є розв’язком рівняння (3.6), і навпаки. У силу накладених на функції умов коефіцієнти рівнянь (3.11), (3.12) мають неперервні похідні до 2-го порядку включно, а тому існують неперервні, разом з похідними до 2-го порядку включно, загальні інтеграли рівняння (3.7) .

Розглянемо область , в усіх точках якої рівняння має один і той же тип. Через кожну точку області проходять дві характеристики. Причому для рівняння гіперболічного типу характеристики дійсні й різні, еліптичного комплексні й різні, а параболічного обидві характеристики дійсні та співпадають між собою. Це дозволяє у даній області звести рівняння до найпростішого канонічного вигляду.

3.3 Зведення до канонічного вигляду рівняння

2-го порядку від двох незалежних змінних

1. Рівняння гіперболічного типу. Для рівнянь гіперболічного типу корені рівняння (3.7) дійсні та різні і характеристичне рівняння (3.7) має дві дійсні та різні сім’ї характеристик

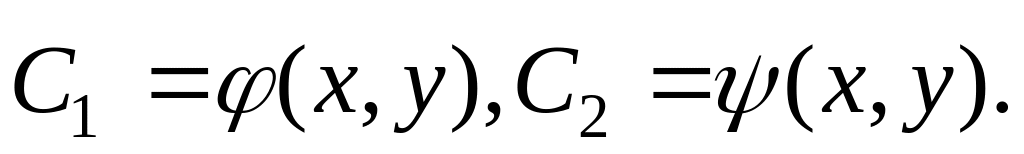
Покажемо, що вони лінійно незалежні, тобто визначник Дійсно, загальні інтеграли є розв’язками рівнянь (3.11) або (3.12), тобто

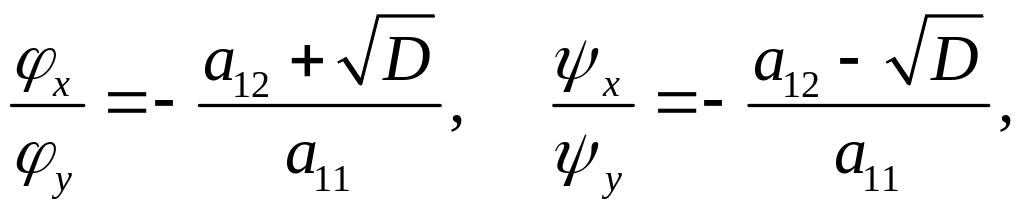(3.13)

або

Згідно з умовою а отже,

або

Із останніх нерівностей маємо

що і потрібно було показати.

Загальні інтеграли системи (3.13) визначають дійсну сім’ю характеристик. Виберемо

, (3.14)

Тоді та , а рівняння (3.1) прийме наступний вигляд після поділу на коефіцієнт при

, (3.14)

де - .

Рівняння (3.14) є першою канонічною формою рівнянь гіперболічного типу.

Зауважимо, що, якщо то рівняння (3.1) уже має вигляд (3.14).

Якщо узяти , , і - нові змінні, можна отримати другу канонічну форму рівняння гіперболічного типу

. (3.15)

2. Для рівнянь параболічного типу і тут рівняння характеристик (3.8) співпадають. Якщо взяти у цьому випадку , , де будь-яка функція, що не залежить від , то при такому виборі змінних рівняння параболічного типу можна привести до канонічної форми

(3.16)

3. Для рівняння еліптичного типу і праві частина рівняння (3.8) комплексно-спряжені.

Нехай – комплексний інтеграл рівняння (3.6) або (3.8). Перейдемо до комплексних змінних, припускаючи що , - комплексно - спряжена до функція. Щоб не мати справи з комплексними змінними, введемо нові зміні і , які дорівнюють , , отже і .

Отже у випадку рівняння еліптичного типу у якості функцій та можна взяти дійсну та уявну частини будь – якого із двох загальних інтегралів рівняння характеристик (3.6) або (3.8).

У цьому випадку ,а .

Рівняння (3.1) після ділення на коефіцієнт при набуває вигляду .

кожне з рівнянь (3.11) розпадається на два лінійні однорідні диференціальні рівняння з частинними похідними першого порядку

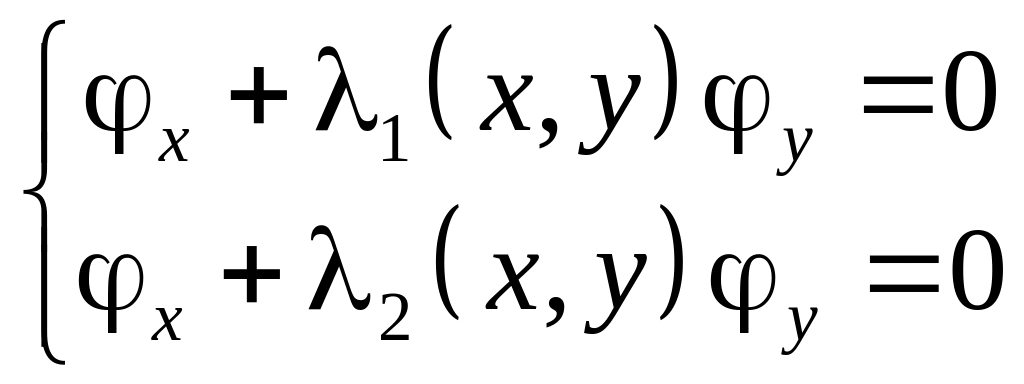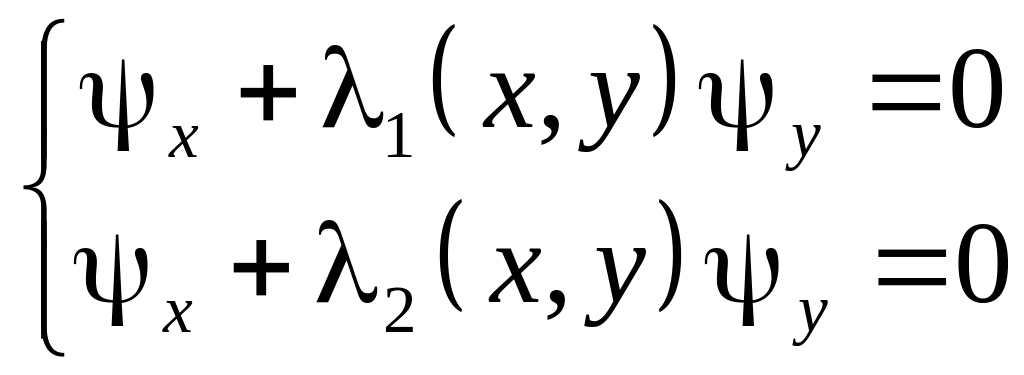; , (3.17)

де 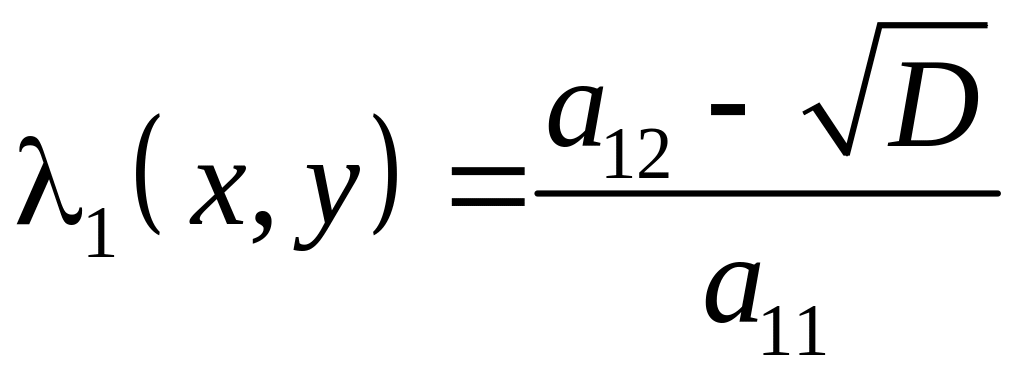; 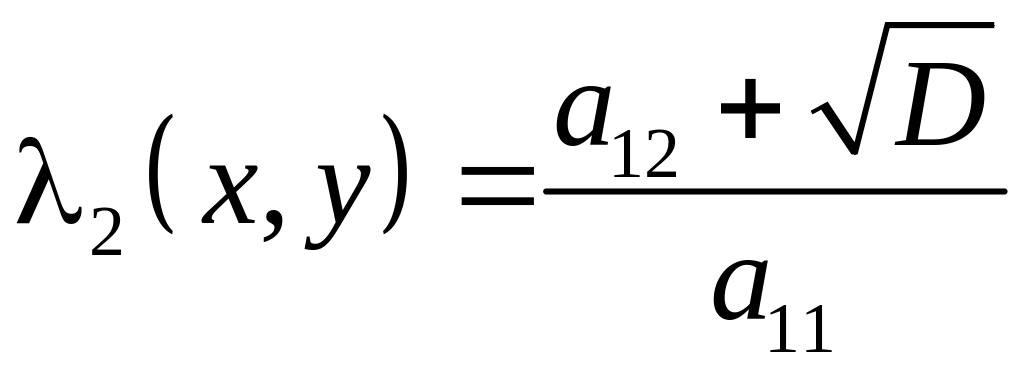(3.18)

Із отриманих систем методом характеристик нескладно знайти функції та (як рівнянь з частинними похідними 1-го порядку)

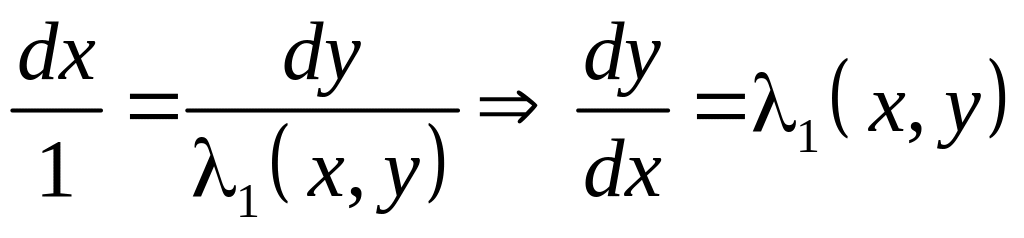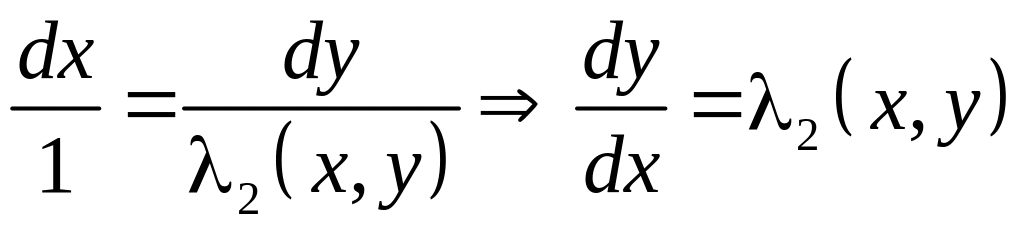, (3.19)

.

Рівняння є диференціальними рівняннями характеристик.

Алгоритм зведення рівняння другого порядку до канонічної форми

1. Визначити коефіцієнти рівняння

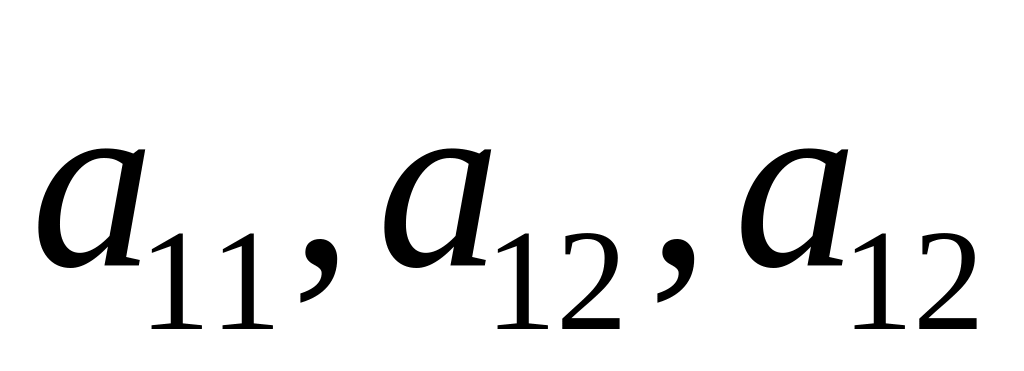
2. Обчислити дискримінант рівняння

3. Визначити тип рівняння

4. Скласти рівняння характеристик (3.6),(3.7) та визначити функції та .

5. Підставити значення функцій та у початкове рівняння та записати канонічну форму рівняння

   0. 5.1 Гіперболічну

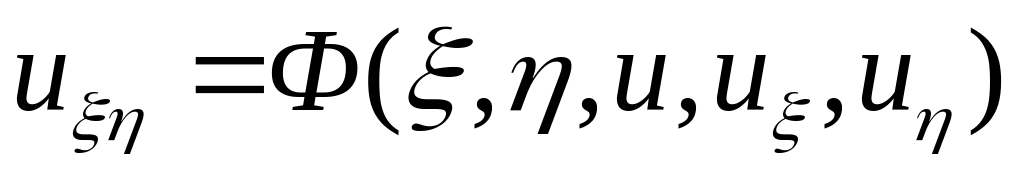
   1. 5.2 Параболічну 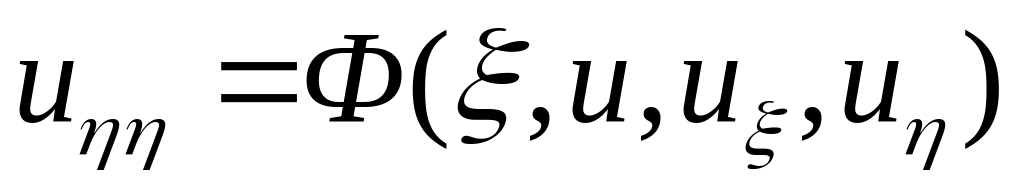або

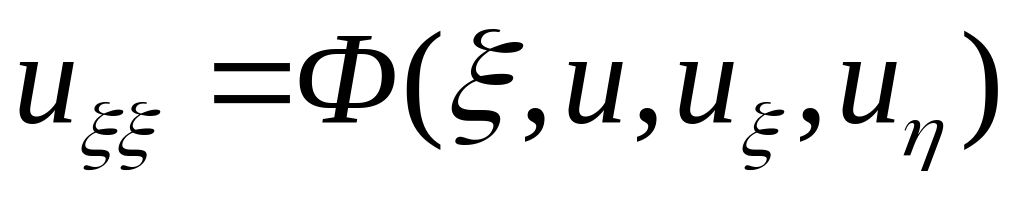
   2. 5.3 Еліптичну

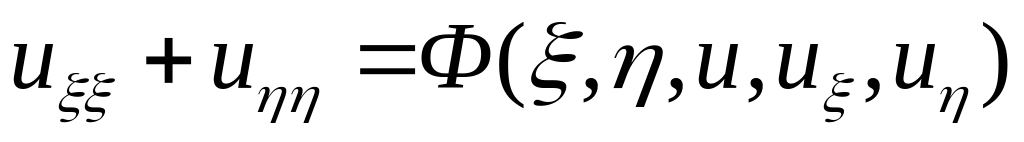
Приклад 3.1

Визначити тип рівняння та звести його до канонічного вигляду

. (3.20)

Розв’язок.

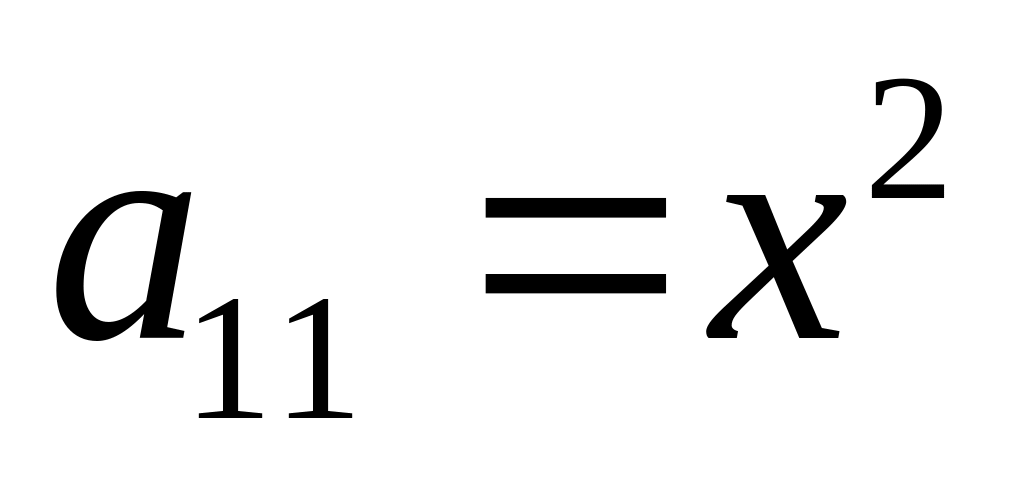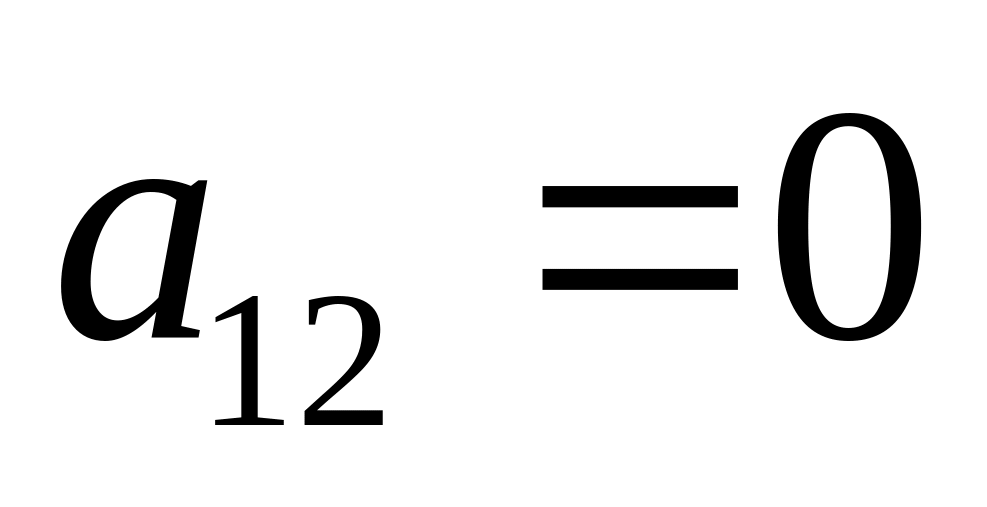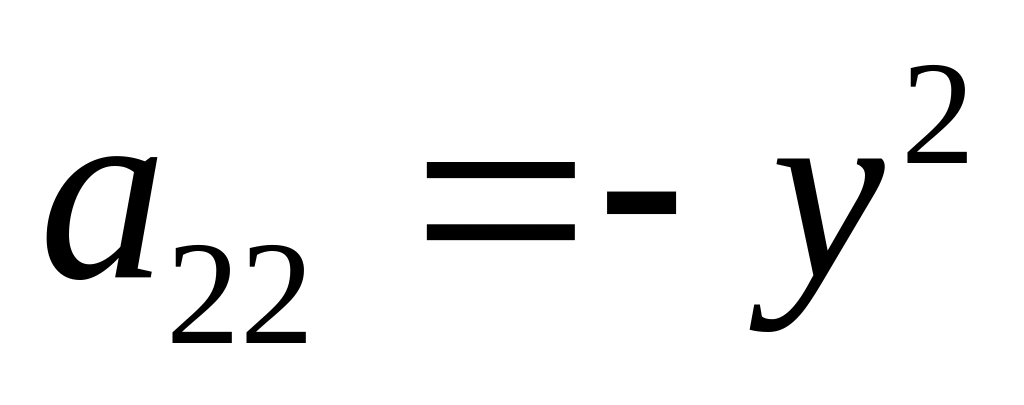1. Тут , , , тому 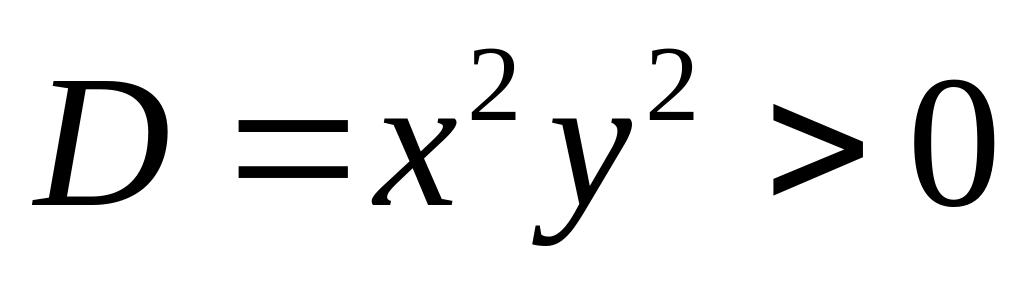, отже, це рівняння гіперболічного типу в .

2. Згідно з (3.18) та (3.19) рівняння характеристик буде

;

3. Звідси рівняння характеристик та , а та - їх загальні інтеграли.

4. Візьмемо ліві частини загальних інтегралів функціями та у заміні змінних. Тут , а і заміна змінних набуває вигляду .

5. Тоді згідно з (3.3) будемо мати

,

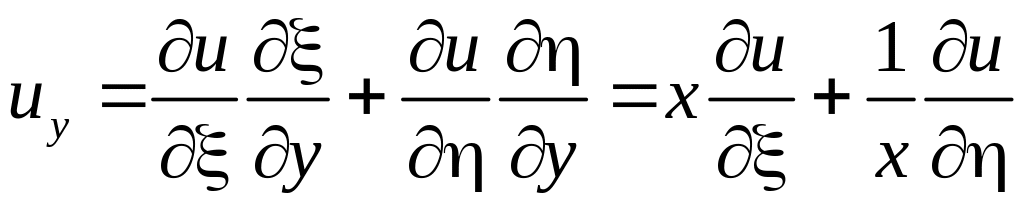
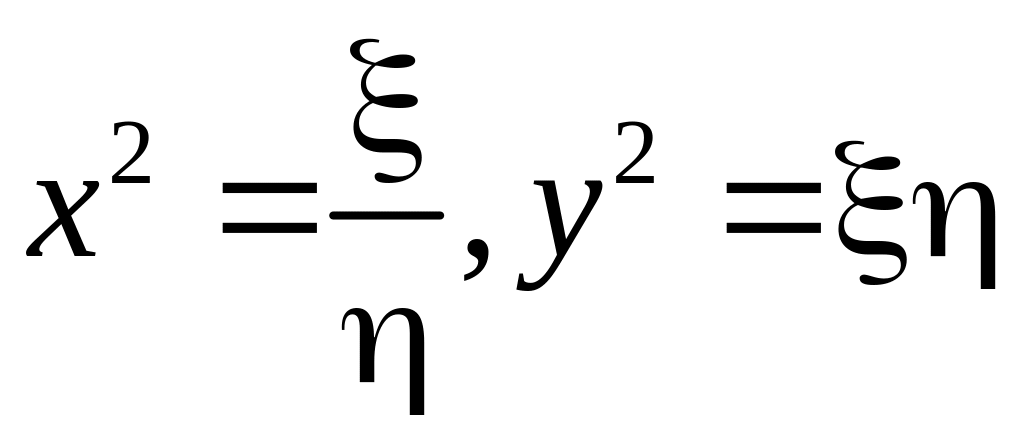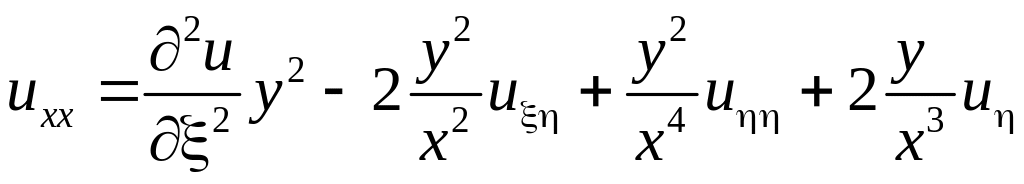, , (3.21)

.

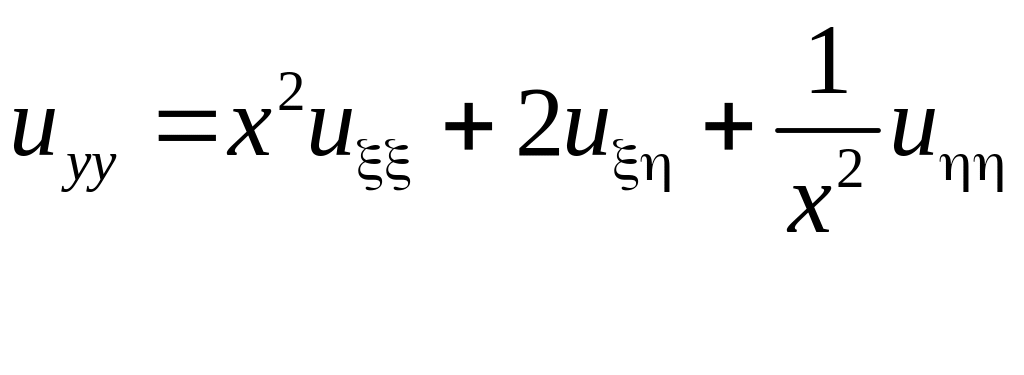Підставивши (3.21) до (3.20), будемо мати канонічний вигляд рівняння .

Приклад 3. 2

Знайти області гіперболічності, еліптичності та параболічності рівняння та визначити характеристики в цих областях.

(3.22)

Розв’язок.

Дискримінант для рівняння (3.22) має вигляд

,

де ;

Корені та поділяють числову вісь на три області, у яких дискримінант змінює знаки.

1. Нехай , , тоді корені та дійсні й різні, а функція додатна. Відповідне перетворення приведе до рівняння (3.19). Отже, область гіперболічності

2. Для будемо мати і рівняння буде мати еліптичний вигляд

3. Для , , пряма складається з точок параболічності

4. Якщо , рівняння в області дійсних чисел розв’язків не має, а тому для маємо область гіперболічності.

Складаємо рівняння характеристик. Підставивши в (3.8), будемо мати

.

Звідси маємо дві характеристики

;

.

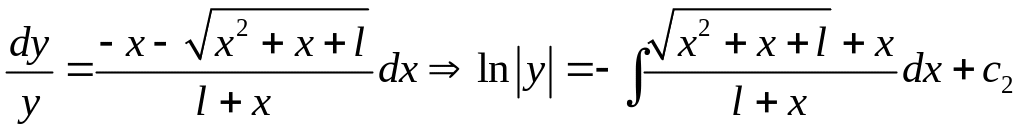Обчисливши інтеграли, будемо мати характеристики в явному вигляді .