2 Диференціальні рівняння з частинними похідними

ПЕРШОГО ПОРЯДКУ

2.1 Основні поняття

Визначення. Співвідношення між незалежними змінними невідомою функцією та її частинними похідними довільного порядку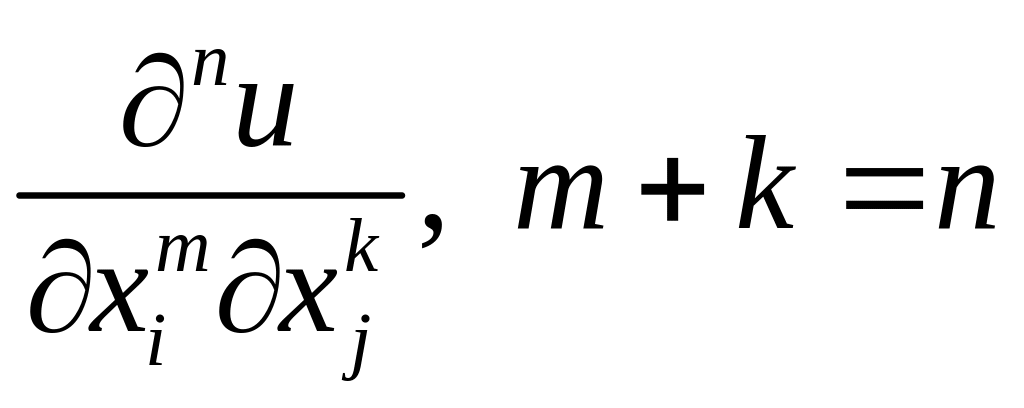 називається диференціальним рівнянням з частинними похідними.

Визначення. Рівняння, що має вигляд

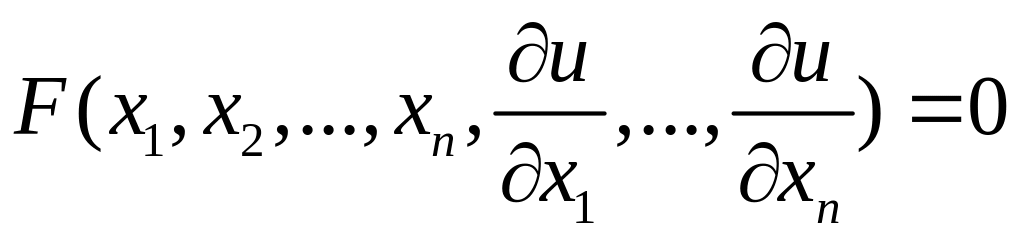, (2.1)

де – невідома функція, називається диференціальним рівнянням з частинними похідними 1-го поряду. У загальному вигляді це буде нелінійне рівняння.

Визначення. Диференційована функція буде розв’язком рівняння (2.1), якщо при підстановці вона перетворює його у тотожність.

Якщо розв’язок рівняння (2.1), то поверхня у просторі змінних називається інтегральною поверхнею рівняння (2.1).

Визначення. Якщо рівняння (2.1) лінійне відносно частинних похідних, але нелінійне відносно невідомої функції , то таке рівняння називається квазілінійним та має вигляд

(2.2)

Якщо у рівнянні (2.2) коефіцієнти не залежать від шуканої функції то таке рівняння називається напівлінійним

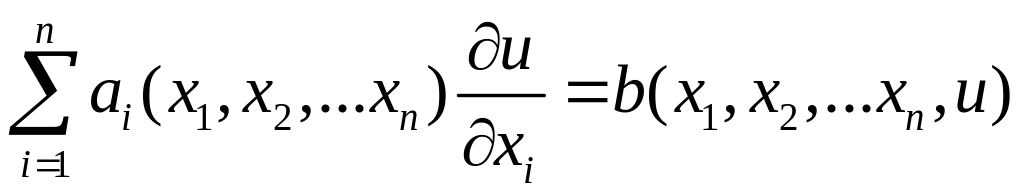
Якщо рівнянні (2.2) функції розглядати як компоненти вектора , а частинні похідні як компоненти вектора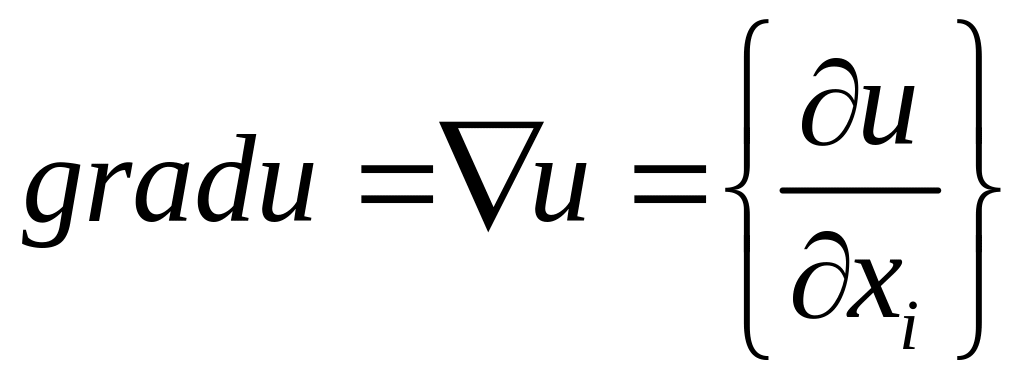 ,то його можна записати у вигляді скалярного добутку ,

або

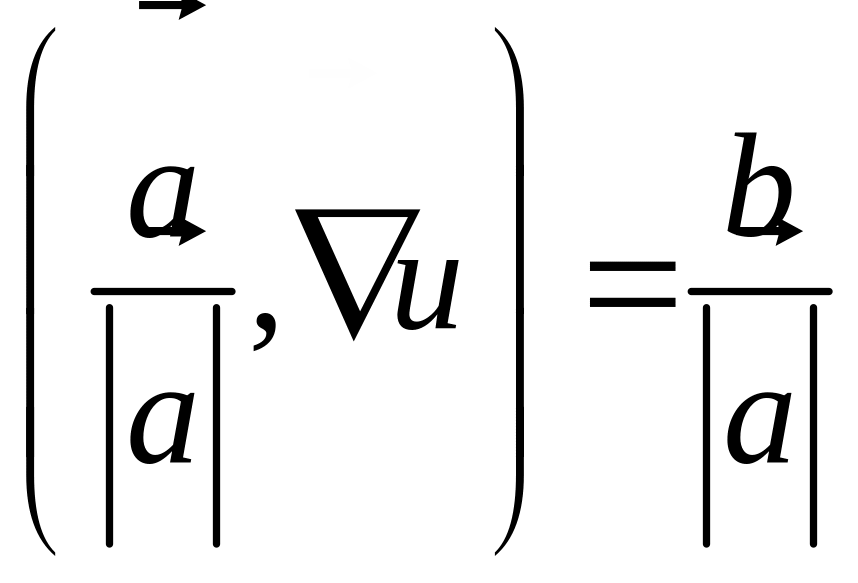(2.3)

Вираз, що стоїть у лівій частині формули (2.3) є похідна функції у напрямі вектора 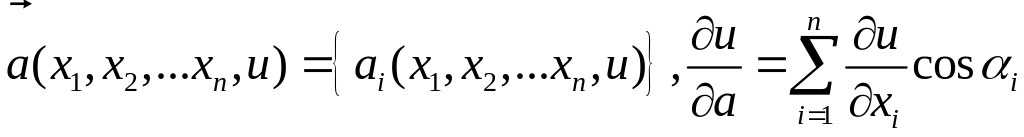. Тому розв’язками рівняння (2.2) будуть функції похідна яких у кожній точці має вигляд та напрям

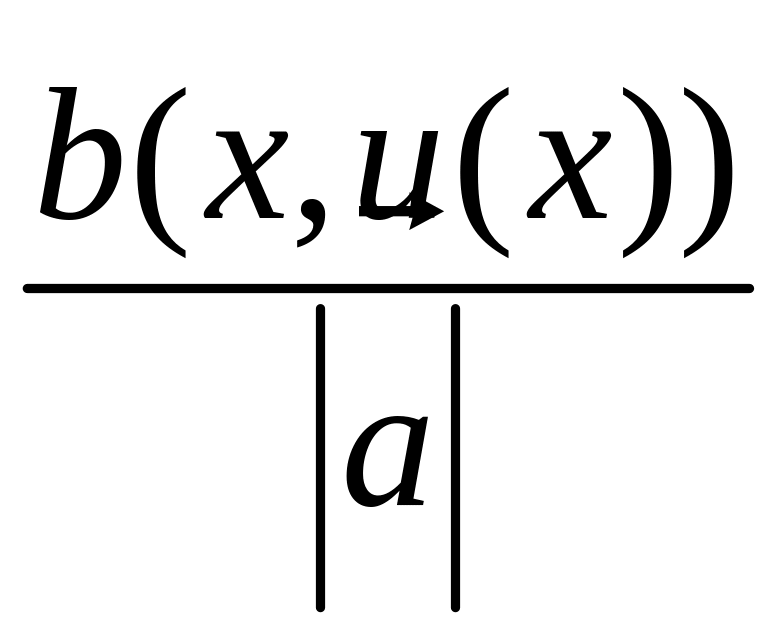
Якщо у рівнянні (2.2) права частина дорівнює нулю то таке рівняння називається квазілінійним

, (2.4)

а якщо у ньому функції не залежать від , то лінійним однорідним рівнянням першого порядку

(2.5)

2.2 Характеристики та їх геометричний зміст. Метод характеристик

Розглянемо напівлінійне рівняння з двома невідомими

, (2.6)

де неперервні функції своїх аргументів у деякій області , що задовольняють у ній умові . Воно лінійне відносно частинних похідних але нелінійне відносно невідомої функції . Рівняння (2.6) можна розглядати як похідну за напрямом деякого змінного вектора. Функції визначають поле напрямів у просторі . У кожній фіксованій точці цього простору ми маємо напрям для якого напрямні косинуси пропорційні функціям . Це поле напрямів визначає сім’ю кривих, для яких будь-яка лінія має у кожній своїй точці дотичну, що співпадає з напрямом поля у цій точці. Це означає ,що розв’язок рівняння (2.6) визначає інтегральну поверхню яка у кожній своїй точці має дотичну площину, напрямні коcинуси якої і пов'язані лінійним рівнянням

(2.7)

та пропорційні функціям .

Згідно рівняння(2.7), дотичні площини усіх інтегральних поверхонь, що проходять через точку належать одному і тому ж пучку площин, вісь яких у точці Р пов’язана співвідношеннями

, (2.8)

Такі пучки та їх вісі називаються пучками і осями Монжа . Точку , через яку проходить направлена вісь Монжа, називають характеристичним лінійним элементом. Напрям осей Монжа утворює у просторі поле напрямів визначених системою звичайних диференціальних рівнянь (2.8) і називається «характеристичними кривими » диференціального рівняння (2.6).

Нехай розв’язок рівняння (2.6) – поверхня у деякій області , а – криві на цій поверхні параметр. Тоді їх диференціальні рівняння для визначення поверхні матимуть наступний вигляд

, , (2.9)

Визначення. Система (2.9) називається характеристичною системою рівняння (2.8), а лінії, що нею визначаються називаються характеристичними або характеристиками рівняння (2.8).

Проекції характеристичних кривих на площину іноді називають характеристичними проекціями.

Зауваження. Параметр на характеристиці рівняння (2.6) визначається з точністю до довільної сталої.

З геометричної точки зору інтегрування диференціального рівняння з частинними похідними (2.6) означає знаходження такої поверхні, дотичні площини до якої у кожній звичайній точці належить пучку Монжа, або у кожній своїй звичайній точці мають напрям вісі Монжа своїм дотичним напрямом. Звідси випливає, що будь-яка поверхня утворена сім’єю характеристичних кривих, що залежать від одного параметра, є інтегральною поверхнею диференціального рівняння з частинними похідними. Метод розв’язку рівняння з частинними похідними, що полягає у зведенні рівняння (2.2),(2.6) до систем (2.8), (2.9) називається методом характеристик.

Так як розв'язок системи (2.8) однозначно визначається початковими значеннями при , то має місце наступна теорема.

Теорема 2.1 Якщо є інтеграл системи (2.8), то функція повинна задовольняти рівняння (2.6).

Справедлива та має місце обернена теорема.

Теорема 2.2 Якщо є розв’язок рівняння (2.6), то є інтеграл або загальний розв’язок системи (2.8).

Висновок. Теореми стверджують, що будь-яка інтегральна поверхня рівняння (2.2),(2.6) утворена сім’єю характеристик.

Алгоритм знаходження загального розв’язку напівлінійного рівняння (2.6).

1. Скласти та розв’язати систему звичайних диференціальних рівнянь (2.8) або (2.9). Якщо немає особливої потреби, параметр можемо не вводити.

2. Виписати загальний розв’язок рівняння (2.6 ). Ним буде функція , або , де два лінійно незалежних інтеграли системи (2.8) або (2.9).