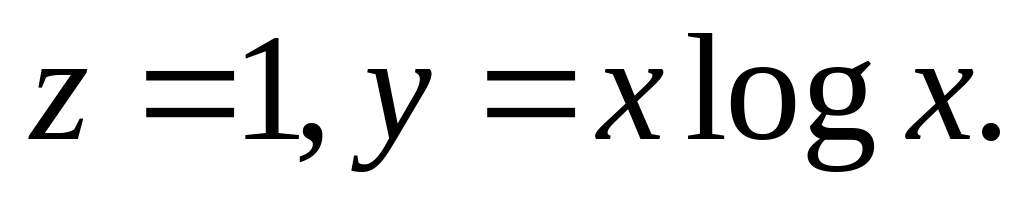2.5 Задача Коші для нелінійних рівнянь
Розглянемо задачу Коші для нелінійного рівняння (2.1)
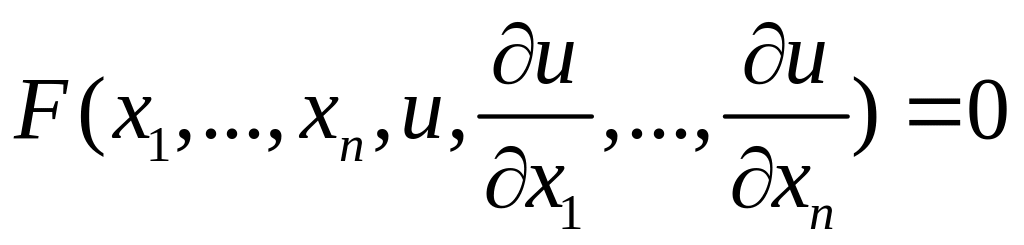 ,
(2.29)
,
(2.29)
де
 функція класу
функція класу![]() ,
визначена на деякій відкритій множині
у просторі змінних
,
визначена на деякій відкритій множині
у просторі змінних
![]() з початковою умовою
з початковою умовою
![]() (2.30)
(2.30)
Тут
![]() – деяка
мірна
неперервна поверхня
– деяка
мірна
неперервна поверхня
![]() без самоперетину, а
без самоперетину, а
![]() ,
неперервна двічі диференційована
функція визначена на поверхні
,
неперервна двічі диференційована
функція визначена на поверхні
![]() .
.
Визначення.
Поверхня
називається регулярною класу
![]() ,
якщо функції
,
якщо функції
![]() у будь-якій точці цієї поверхні.
у будь-якій точці цієї поверхні.
Нехай
функція
![]() класу
є розв’язком задачі Коші (2.29), (2.30).
Підставивши її в (2.29), отримаємо тотожність.
Продиференціюємо її за змінними
класу
є розв’язком задачі Коші (2.29), (2.30).
Підставивши її в (2.29), отримаємо тотожність.
Продиференціюємо її за змінними
![]()
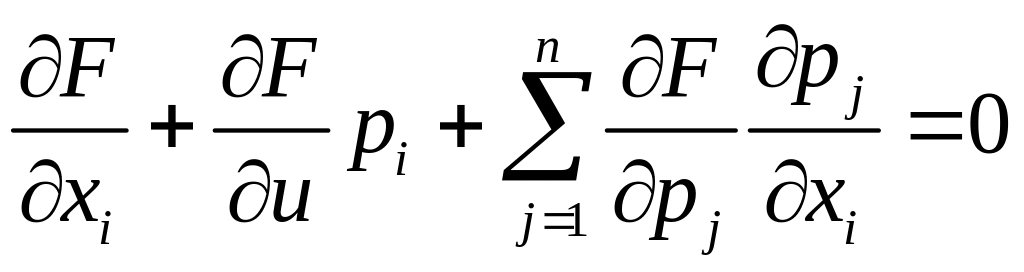 (i
=
1 ., n) (2.31)
(i
=
1 ., n) (2.31)
Оскільки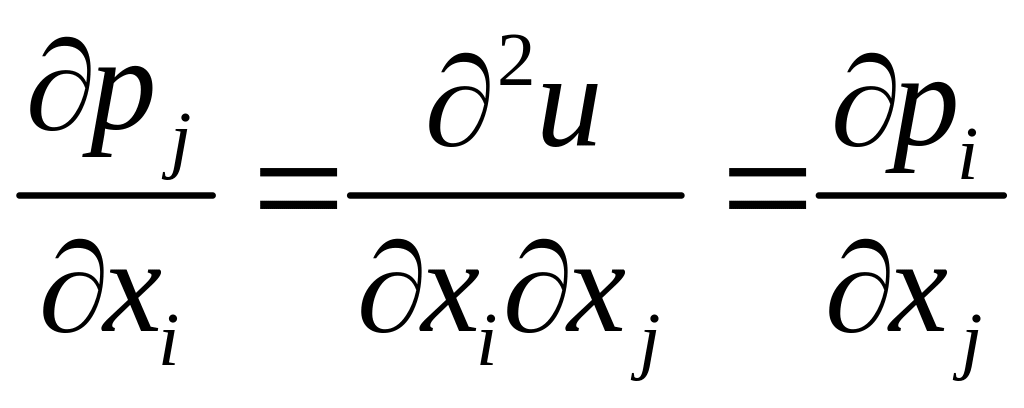 ,
рівність (2.31 ) можна записати у вигляді
,
рівність (2.31 ) можна записати у вигляді
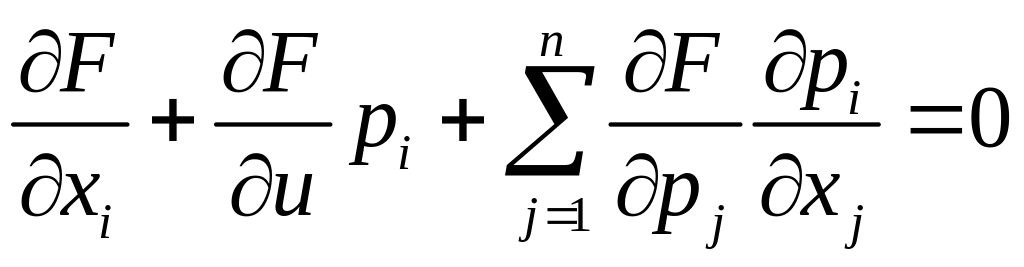 (i
=
1 ., n)
(i
=
1 ., n)
З
цих рівнянь видно, що функції
![]() задовольняють системам квазілінійних
рівнянь з «однаковою головною частиною»
задовольняють системам квазілінійних
рівнянь з «однаковою головною частиною»
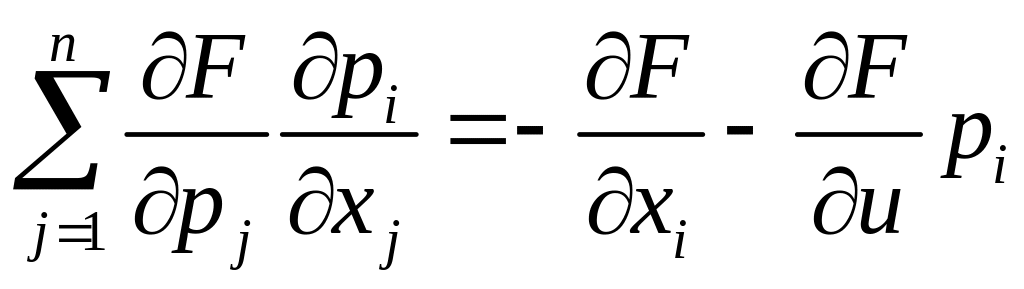 (i
=
1 ., n) (2.32)
(i
=
1 ., n) (2.32)
Розглянемо
розв’язок
![]() уздовж
траєкторій системи диференціальних
рівнянь
уздовж
траєкторій системи диференціальних
рівнянь
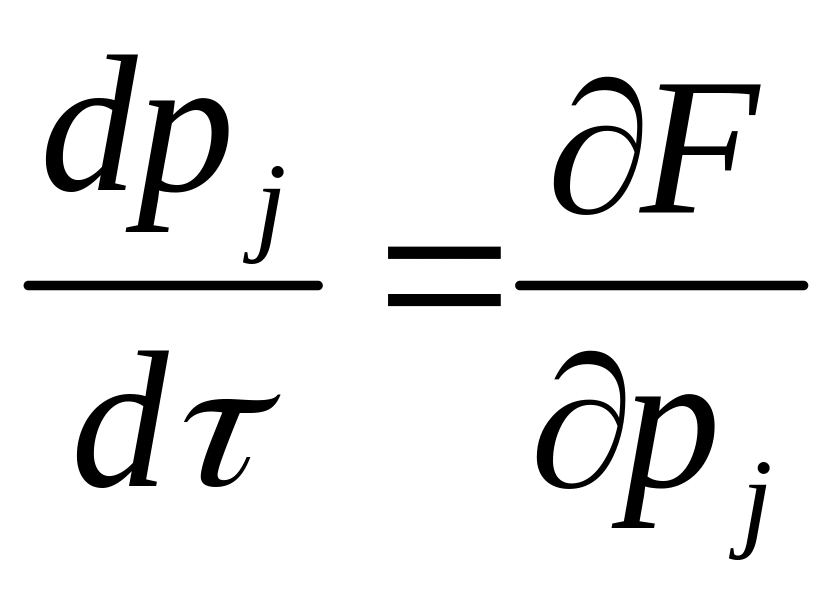 (j
=
1 ., n) (2.33)
(j
=
1 ., n) (2.33)
Рівняння (2.32) у цьому випадку можна записати у вигляді
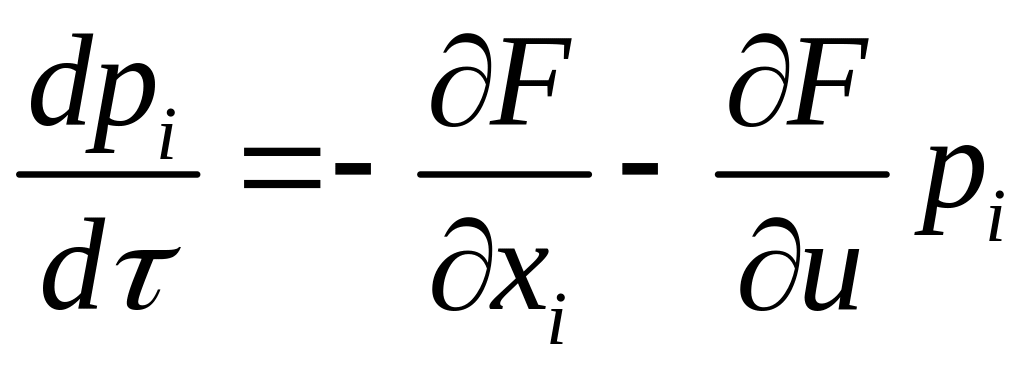 (i
=
1 ., n) (2.34)
(i
=
1 ., n) (2.34)
Скориставшись співвідношенням (33), обчислимо
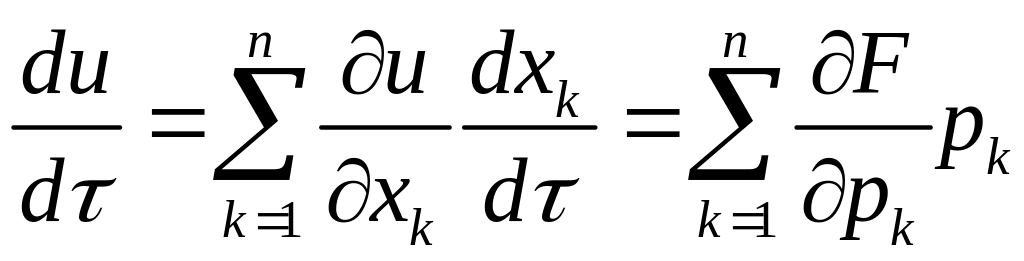 (2.35)
(2.35)
Отже, якщо розв’язок задачі Коші (2.29), (2.30), то уздовж будь-якої траєкторії системи рівнянь (2.33) функції та (i = 1, n), задовольняють умовам (2.34) та (2.36).
Система
з
![]() звичайних
диференціальних рівнянь (2.33), (2.34), та
(2.35) називається характеристичною
системою рівняння (2.29), а її траєкторії
у просторі змінних
звичайних
диференціальних рівнянь (2.33), (2.34), та
(2.35) називається характеристичною
системою рівняння (2.29), а її траєкторії
у просторі змінних
![]() –
характеристиками цього рівняння .
–
характеристиками цього рівняння .
Розглянемо
спосіб знаходження розв’язку задачі
Коші (2.29), (2.30) Вважаючи, що
–
розв’язок даної задачі Коші, і
диференціюючи (2.30) по
![]() (
(![]() =
1 .,
),
отримаємо
=
1 .,
),
отримаємо
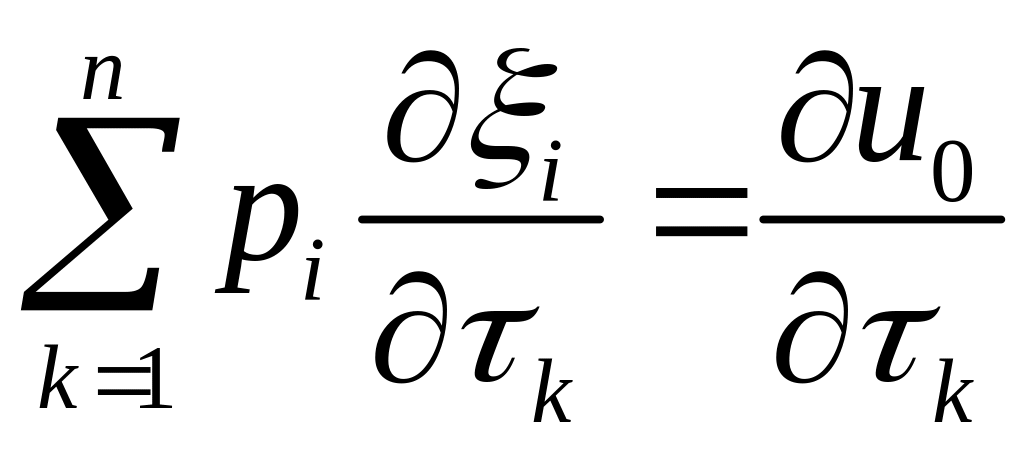 (2.36)
(2.36)
Оскільки функція – розв’язок задачі Коші (2.29) (2.30), то і повинні задовольняти рівнянню
![]() (2.37)
(2.37)
Припустимо, що
![]() (
(![]() )
(2.38)
)
(2.38)
неперервний
розв’язок системи рівнянь (2.36), (2.37), для
якого на поверхні
визначник
![]() відмінний від нуля
відмінний від нуля
![]()

![]() (2.39)
(2.39)
Якщо
![]() ,
то розв’язуємо задачу Коші для
характеристичної системи (2.33) - (2.35) з
наступними початковими умовами
,
то розв’язуємо задачу Коші для
характеристичної системи (2.33) - (2.35) з
наступними початковими умовами
![]() (i
=
1, n)
(i
=
1, n)
![]() ,
,
![]() (j
=
1, n)
(j
=
1, n)
Розв’язок цієї задачі існує, єдиний та має вигляд
![]() (
)
(
)
![]() (2.40)
(2.40)
![]() (
(![]() )
)
Перші
дві групи рівнянь з (2.40) визначають
розв’язок задачі Коші (2.29), (2.30) (заданий
параметрично) у деякому околі на поверхні
![]() ,
і цей розв’язок єдиний, якщо вибрані
функції
,
і цей розв’язок єдиний, якщо вибрані
функції
![]() .
.
Зауваження.
Система рівнянь (2.35), (2.36), взагалі кажучи, розв’язується неоднозначно відносно , тому і задача Коші (2.29), (2.30) може мати більше ніж один розв’язок.
У додатках часто зустрічається задача Коші для нелінійного рівняння вигляду
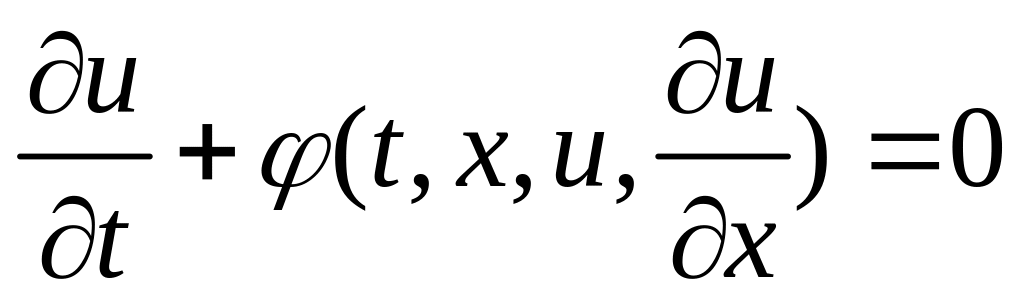 з початковою умовою
з початковою умовою
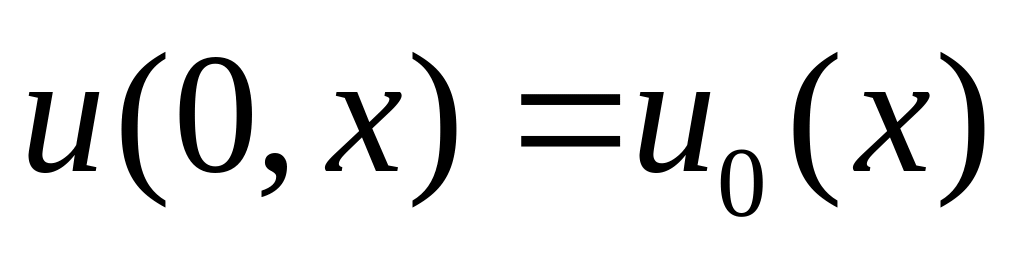 .
.
В цьому випадку рівняння (2.36), (2.37) мають вигляд
![]() ,
,
![]()
Очевидно,
що ці рівняння розв’язуються однозначно
відносно
![]() та
та![]() ,
і тому розв’язок даної задачі Коші
єдиний. Якщо функція
,
і тому розв’язок даної задачі Коші
єдиний. Якщо функція
![]() не залежить від u,
то розв’язок нелінійного рівняння
зведеться
до розв’язку деякого квазілінійного
рівняння. Насправді, функція
не залежить від u,
то розв’язок нелінійного рівняння
зведеться
до розв’язку деякого квазілінійного
рівняння. Насправді, функція
![]() задовольняє наступному квазілінійному
рівнянню
задовольняє наступному квазілінійному
рівнянню
![]()
Приклад 2.6
Розв’язати задачу Коші для рівняння
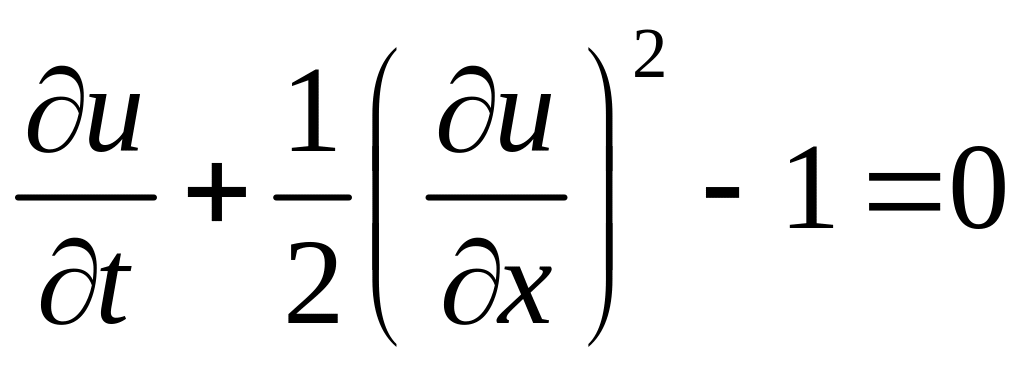 (2.41)
(2.41)
![]() =
=![]() ,
,
![]() .
(2.42)
.
(2.42)
Розв’язок.
Покладемо
![]() .
Позначаючи
.
Позначаючи![]() ,
,![]() ,
отримаємо наступну характеристичну
систему, що відповідає рівнянню (2.41)
(маємо п’ять невідомих , об’єднаних у
п’ять рівнянь)
,
отримаємо наступну характеристичну
систему, що відповідає рівнянню (2.41)
(маємо п’ять невідомих , об’єднаних у
п’ять рівнянь)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (2.43)
(2.43)
Поверхня
у даному випадку це площина
![]() .
Її рівняння можна записати у вигляді
.
Її рівняння можна записати у вигляді
![]() ,
де
,
де
![]() - параметр.
- параметр.
Початкові
умови для
![]() і
і
![]() мають вигляд (див. (2.36), (2.37))
мають вигляд (див. (2.36), (2.37))
![]()
![]()
Отже, для системи рівнянь (2.43) потрібно розв’язувати задачу Коші з початковими умовами
![]() ,
,![]() ,
,
,
,![]()
![]() (2.44)
(2.44)
Інтегруючи цю систему, отримуємо
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
звідки,
в силу (2.44)
![]()
![]()
![]()
![]()
![]() .
.
Розв’язок задачі Коші (2.41), (2.42) можна записати у вигляді
![]() ,
,
![]() (2.45)
(2.45)
![]() .
.
Виключаючи з рівнянь (2.45) параметри і , отримаємо
![]() .
(2.46)
.
(2.46)
Безпосередньою підстановкою легко переконатися, що (2.46) є розв’язок задачі Коші (2.41) ,(2.42).
Відмітимо,
що цей розв’язок визначений у напів
площині
![]()
![]() .
При
.
При
![]() маємо також розв’язок рівняння (2.41),
але він не задовольняє початковій умові
(2.42), оскільки область визначення цього
рівняння не містить пряму
.
маємо також розв’язок рівняння (2.41),
але він не задовольняє початковій умові
(2.42), оскільки область визначення цього
рівняння не містить пряму
.
Контрольні питання
Який вигляд має однорідне диференціальне рівняння першого порядку з частинними похідними?
Який вигляд має характеристичне рівняння для рівняння першого порядку з частинними похідними?
Що таке загальний та частинний розв’язок рівняння першого порядку з частинними похідними?
Як знайти розв’язок задачі Коші для рівняння першого порядку з частинними похідними?
У чому полягає задача інтегрування рівняння з частинними похідними?
Чим відрізняється загальний розв’язок звичайного диференціального рівняння від загального розв’язку диференціального рівняння з частинними похідними?
У чому полягає задача Коші для диференціального рівняння з частинними похідними першого порядку?
Як формулюються умови для знаходження єдиного розв’язку задачі Коші для диференціального рівняння з частинними похідними першого порядку?
Знайти загальний розв’язок рівняння першого порядку з частинними похідними
9.1![]()
9.2
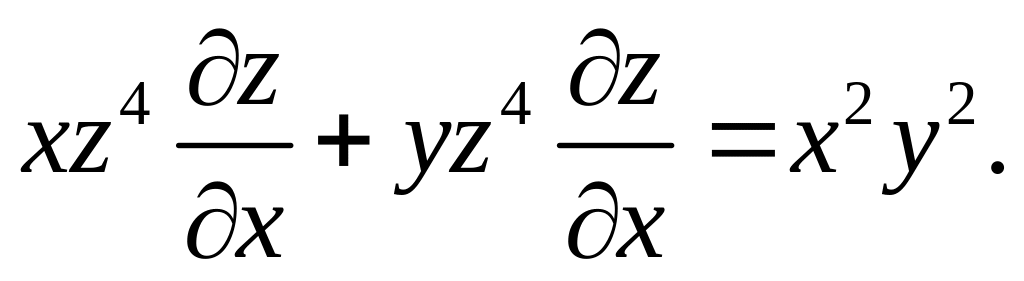
9.3![]()
9.4
![]()
9.5![]()
9.6![]()
9.7![]()
9.8![]()
9.9![]()
9.10![]()
9.11![]()
9.12![]()
Як знайти частинний розв’язок рівняння першого порядку з частинними похідними?
Знайти поверхню, яка задовольняє рівнянню
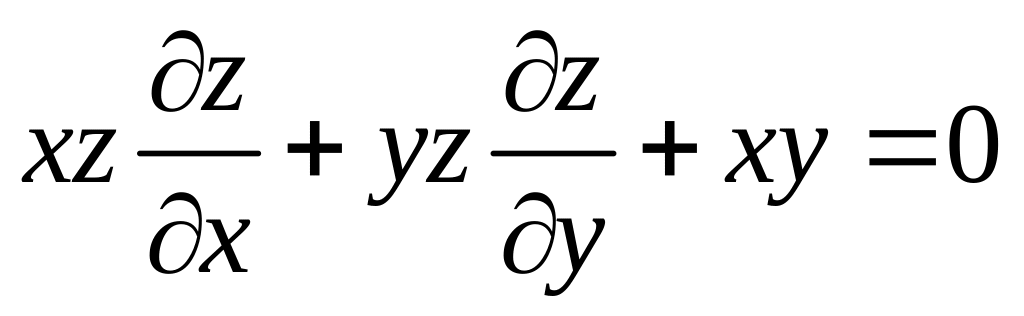 і проходить через криву
і проходить через криву

Знайти поверхню, яка задовольняє рівнянню
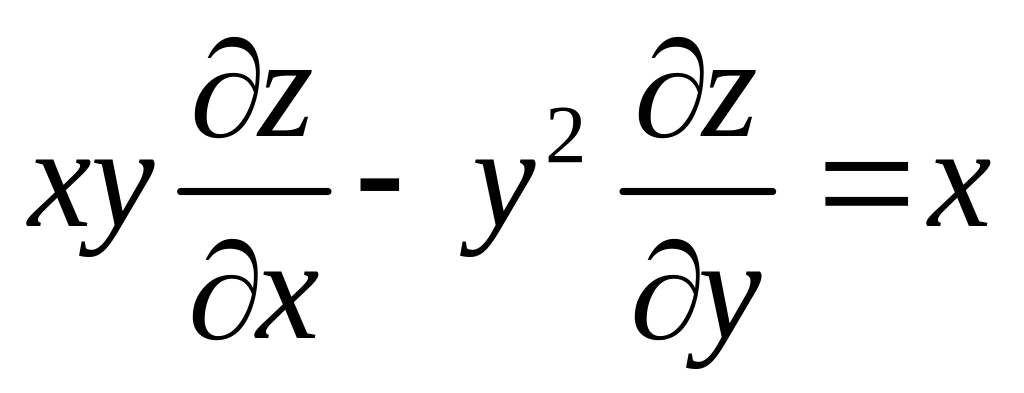 і проходить через криву
і проходить через криву

Знайти поверхню, яка задовольняє рівнянню
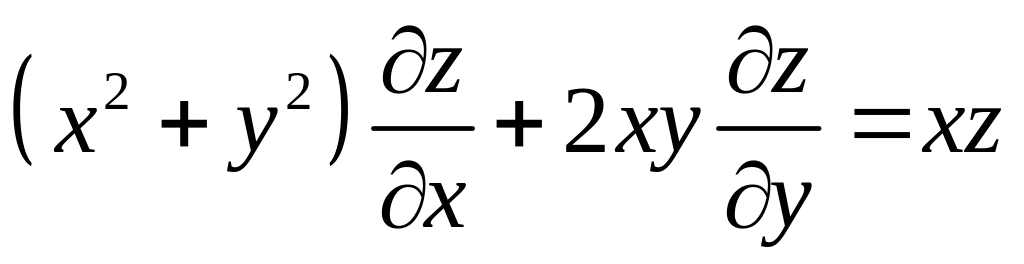 і проходить через криву
і проходить через криву
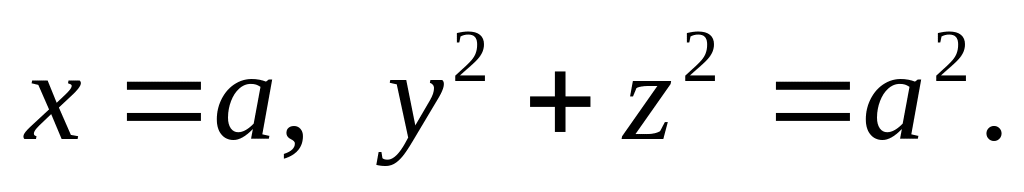
Знайти поверхню, яка задовольняє рівнянню
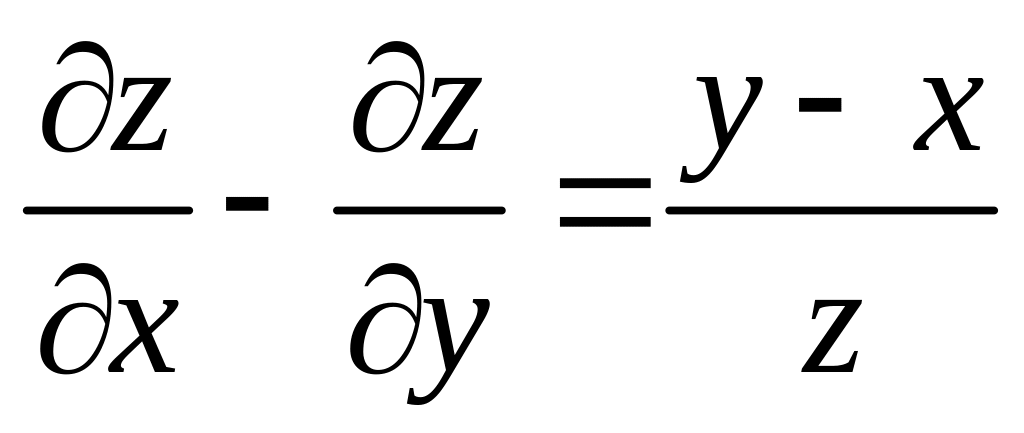 і проходить через криву
і проходить через криву
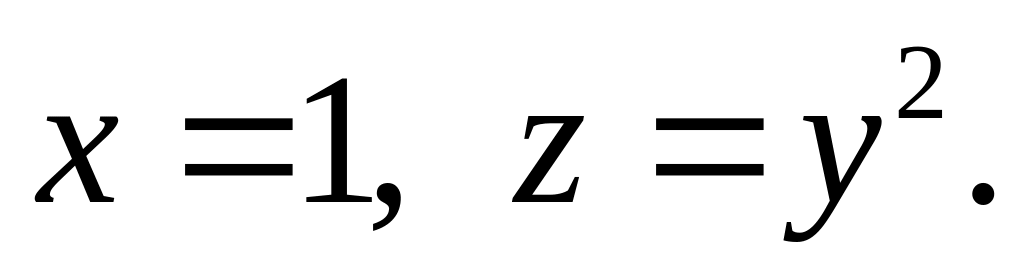
Знайти поверхню, яка задовольняє рівнянню
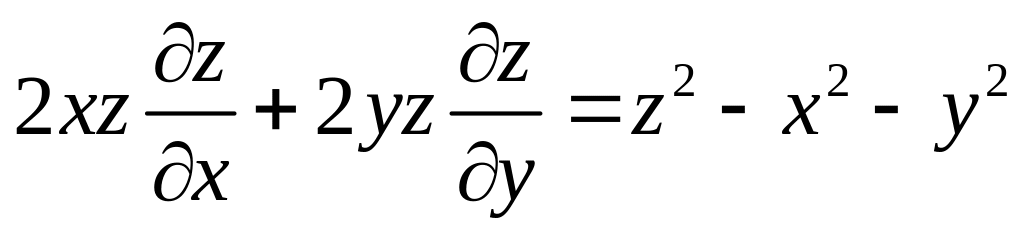 і проходить через криву
і проходить через криву
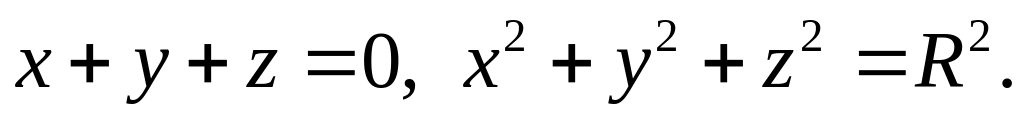
Знайти поверхню, яка задовольняє рівнянню
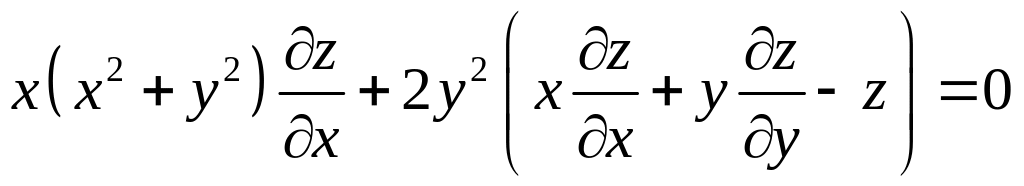 і проходить через криву
і проходить через криву

Знайти загальне рівняння поверхонь, які мають властивість: дотична площина у довільній точці M перетинає вісь у точці N, такій, що відношення
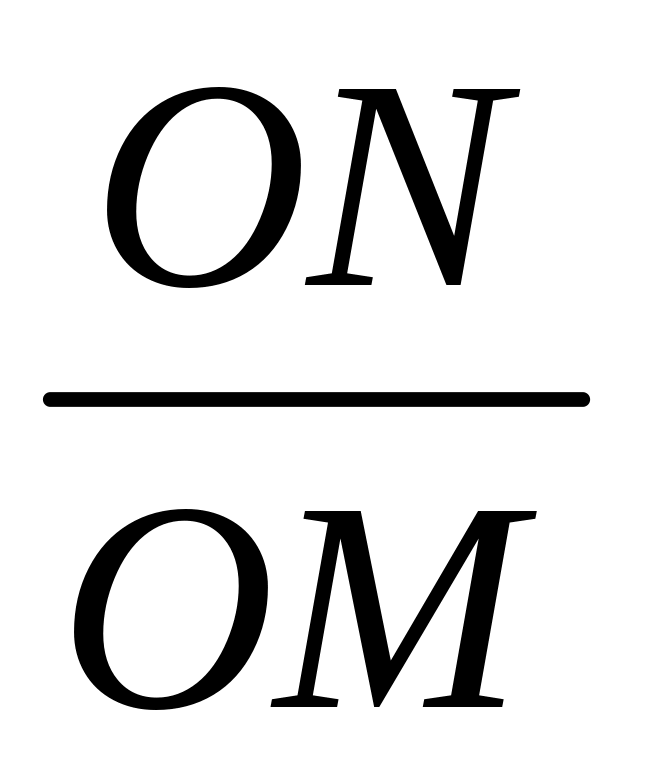 стале та дорівнює K.
Знайти поверхню, яка проходить через
гвинтову лінію на круговому прямому
циліндрі з віссю OZ.
стале та дорівнює K.
Знайти поверхню, яка проходить через
гвинтову лінію на круговому прямому
циліндрі з віссю OZ.Знайти поверхні, для яких дотична площина у довільній точці M перетинає вісь у точці N, рівновіддаленій від початку координат O і точки M.
Знайти поверхні, на яких слід нормалі у точці M на площині XOY рівно віддалений від початку координат O і точки M.
Якщо P – проекція точки M на поверхні на площину , а Q – проекція M на вісь , то площина, дотична до поверхні в M, паралельна прямій PQ. Знайти загальний вигляд поверхонь і поверхню, яка містить криву