3 Рівняння з частинними похідними 2-го порядку

3.1 Канонічні форми запису рівнянь

Означення. Рівнянням з частинними похідними другого порядку з двома невідомими змінними називається співвідношення між невідомою функцією u(x,y) та її частинними похідними до другого порядку включно

.

Означення. Рівняння називається квазілінійним, якщо воно лінійне відносно старших похідних

(3.1)

Означення. Рівняння називається лінійним, якщо воно лінійне відносно невідомаї функції та всих похідних

, (3.2)

де – функції змінних від x та y.

Означення. Рівняння (3.2) називається однорідним, якщо .

Означення. Всяка двічі неперервно-диференційовна в області визначення рівняння (3.1) функція яка, будучи підставлена в дане рівняння замість невідомої функції та її частинних похідних, перетворює його в тотожність називається регулярним розв’язком рівняння (3.1)

Надалі розглядатимемо тільки регулярні розв’язки.

Приклад. Розглянемо диференціальне рівняння

Рівність виконується, якщо , тобто є розв’язком даного рівняння.

Легко бачити, що сума довільних двічі неперервно-диференційованих функцій

та є розв’язком диференціального рівняння

Очевидно, рівняння розв’язку не має.

Як видно із наведених прикладів, диференціальні рівняння можуть мати нескінченну множину розв’язків. Тому, коли фізична або інша задача зводиться до рівняння з частинними похідними, то для однозначного її розв’язку необхідно до рівняння приєднати деякі додаткові умови, які випливають із умови задачі.

Розглянемо квазілінійне рівняння (3.1). Усі диференціальні рівняння вигляду (3.1) можуть бути розділені на три основні типи. В кожному із них за допомогою заміни незалежних змінних рівняння (3.1) зводиться до найпростішого-канонічного вигляду. Тому при вивченні рівнянь з двома незалежними змінними обмежимося надалі дослідженням їх канонічних форм.

Для зведення рівняння (3.1) до простішого вигляду введемо нові незалежні змінні , , які є неперервними функціями та допускають обернене перетворення. Підставивши їх у рівняння (3.1) можна одержати нове рівняння еквівалентне початковому.

Постає питання, як вибрати функції та , так щоб рівняння (3.1), (3.2) набуло найпростішої форми. Скористаємося формулами диференціювання складних функцій. Перетворюючи похідні до нових змінних, одержуємо

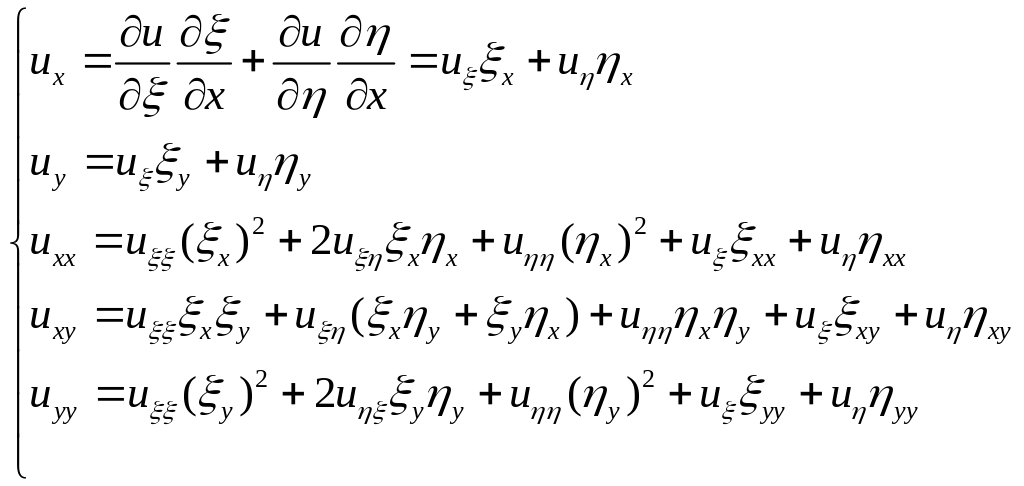(3.3)

Підставляємо (3.3) до (3.2), отримаємо

, (3.4)

де ,

, (3.5)

.

Для того щоб рівняння (3.4) набуло більш простої форми, змінні і підбираються так, щоб один із коефіцієнтів . Підберемо і так, щоб .

Перетворення змінних , повинно бути таким, щоб функції та були двічі диференційованими, і для яких в області перетворення якобіан перетворення задовольняв умові

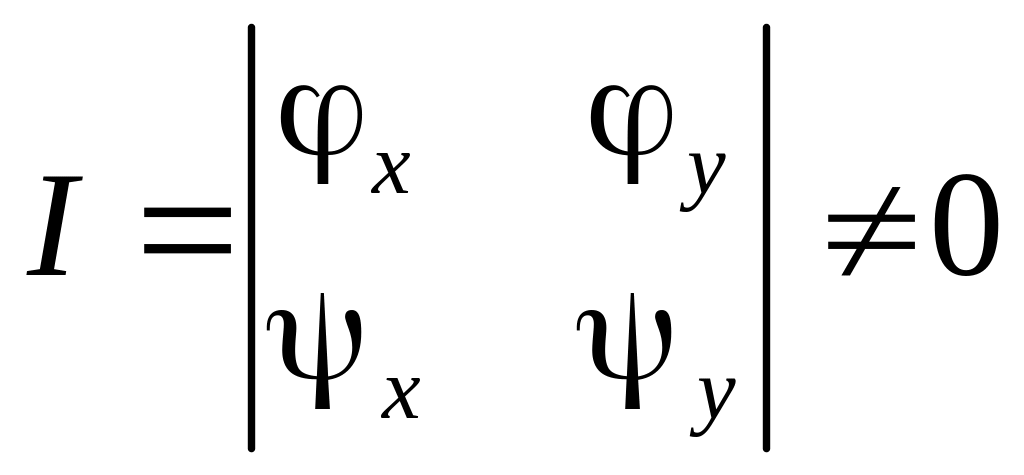
Після перетворення (3.3) нескладно довести, що виконується тотожність для дискримінантів рівнянь (3.2) і (3.4)

Розглянемо рівняння

(3.6)

Нехай – частинний розв’язок цього рівняння. Якщо взяти , то коефіцієнт буде дорівнювати нулю. Отже, задача про вибір нових незалежних змінних пов’язана з розв’язком рівняння (3.5).

Мають місце наступні леми

1. Якщо є частинним розв’язком рівняння (3.6), то співвідношення 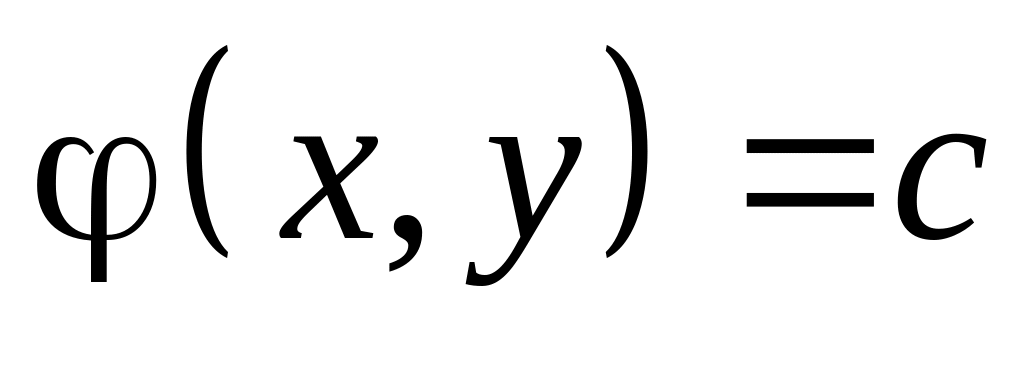є загальним інтегралом звичайного диференціального рівняння

. (3.7)

2. Якщо є загальний інтеграл рівняння (3.6), то функція 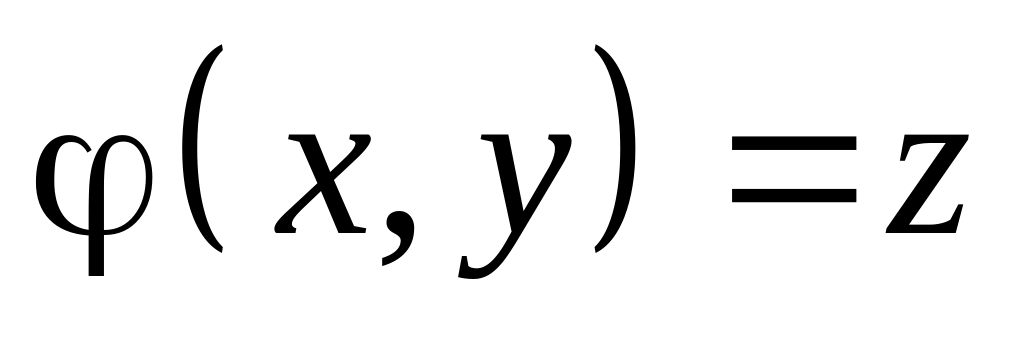задовольняє рівнянню (3.6).

Узявши , де - загальний інтеграл рівняння (3.7), ми перетворюємо (обертаємо) на нуль коефіцієнт при . Якщо є другим лінійно незалежним загальним інтегралом рівняння (3.7), то, узявши , ми обертаємо на нуль коефіцієнт при .