2.3 Загальний розв’язок однорідного диференціального рівняння з частинними похідними

Розглянемо однорідне рівняння (2.5). Його інтегрування зводиться до розв’язання наступної системи звичайних диференціальних рівнянь

(2.10)

де .

Визначивши всі інтеграли системи (2.10) отримаємо розв’язок, що містить довільну сталу . Знайшовши з цих розв’язків отримаємо лінійно незалежну функцію

(2.11)

Теорема 2.3 Всякий розв’язок системи (2.10) є розв’язком однорідного рівняння (2.5) і навпаки: всякий розв’язок однорідного рівняння (2.5) є розв’язком системи (2.10).

Теорема 2.4 Однорідне рівняння (2.5) та рівняння (2.10) мають лінійно незалежних розв’язків, а всі інші розв’язки можна записати у вигляді

(2.12)

Висновок: Розв’язок , де - довільна функція є загальним розв’язком або інтегралом однорідної системи.

Звідси алгоритм інтегрування однорідного рівняння

1. Скласти систему звичайних диференціальних рівнянь (2.10) та знайти її розв’язок.

2. Отримані розв’язки системи (2.10) записати у вигляді (2.12) .

Зауваження 1 Загальний розв’язок звичайного диференціального рівняння містить довільні сталі, а розв’язок рівняння в частинних похідних – довільні функції.

Зауваження 2 Це правило зберігається і коли однорідне рівняння містить шукану функцію . Тоді до розв’язків (2.11) додається ще один – .

Для однорідного рівняння з частинними похідними з двома невідомими

(2.13) маємо відповідне звичайне диференціальне рівняння

Якщо це рівняння має аналітичний розв’язок, то його можна записати у вигляді , а загальний інтеграл у вигляді

(2.14)

Приєднавши до (2.14) самоочевидний розв’язок

, визначимо сім’ю інтегральних поверхонь рівняння (2.13) у вигляді .

Приклад 2.1

Знайти загальний інтеграл .

Розв’язок. Згідно алгоритму, складаємо рівняння

, або . Приєднуємо . Тоді загальний інтеграл записуємо у вигляді або або .

Приклад 2.2.

Знайти загальний розв’язок рівняння

Розв’язок.

Складаємо систему звичайних диференціальних рівнянь, відповідну заданому рівнянню

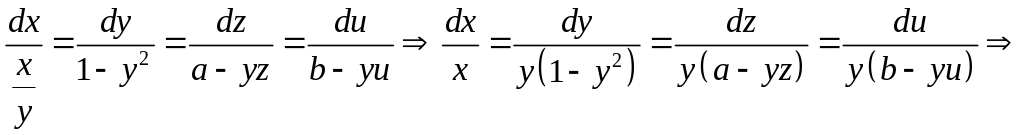
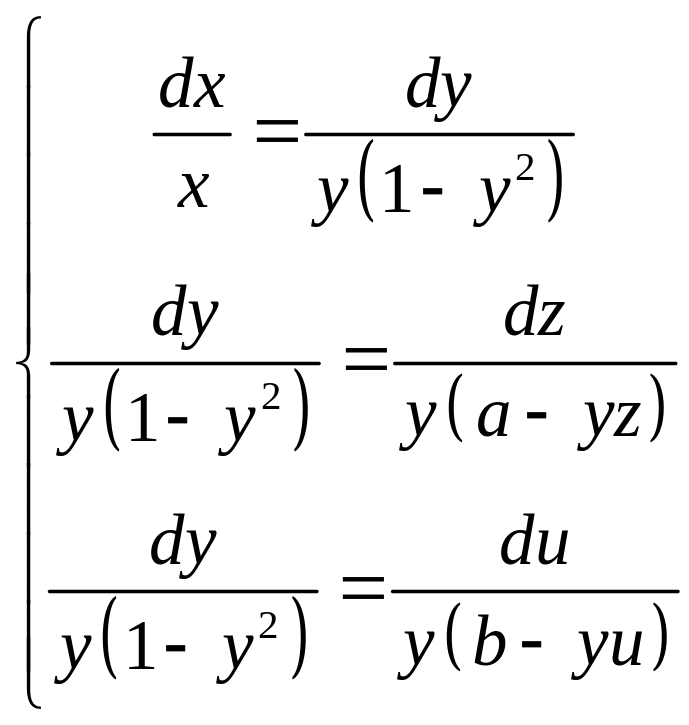
Шукаємо розв’язок кожного рівняння отриманої системи окремо.

2.2.1

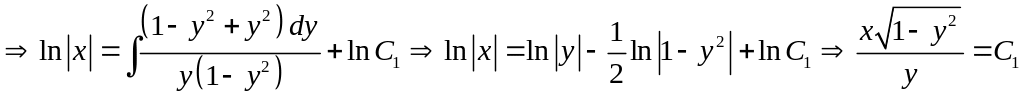
2.2.2

Вважаючи, що , маємо

Це лінійне диференціальне рівняння першого порядку. Розв’яжемо його, застосувавши підстановку Бернуллі.

Покладемо

Знайдемо функцію за умови

Підставляємо значення для в рівняння

Отже, маємо:

Скориставшись співвідношенням між оберненими тригонометричними функціями

та ,

будемо мати .

2.2.3

Покладемо та помножимо обидві частини рівняння на

Це лінійне диференціальне рівняння першого порядку. Розв’язуючи його як і попереднє, отримаємо розв’язок у вигляді

Отже, загальний розв’язок рівняння можна записати у вигляді

.

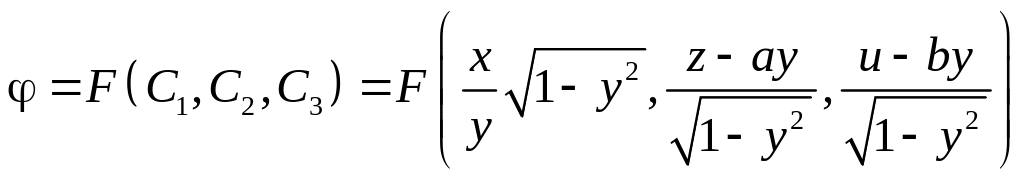Приклад 2.3

Знайти загальний розв’язок рівняння

Розв’язок. Складемо систему рівнянь

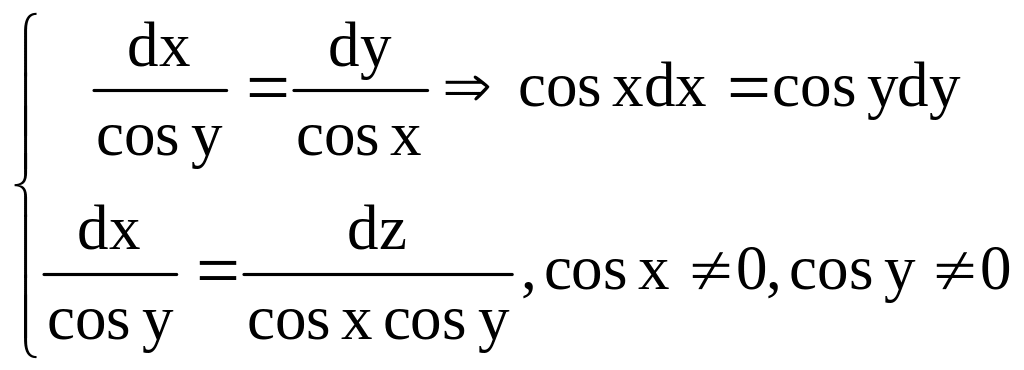
Отже

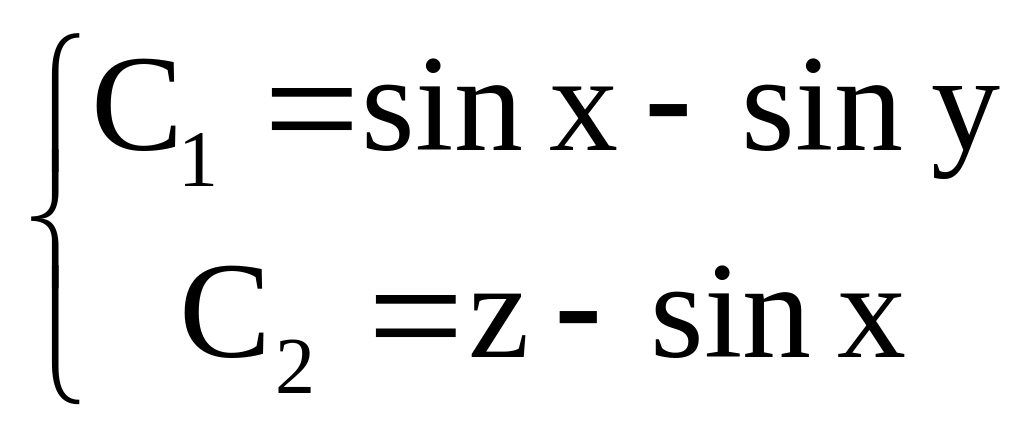
Звідси загальний розв’язок системи можна записати у вигляді

або