4. Построение зависимостей давления, плотности, температуры, числа Маха и скоростного коэффициента от продольной координаты.
Рассмотрим
для примера процедуру построения
давления как функции продольной
координаты, совпадающей с осью симметрии
сопла (остальные параметры строятся
аналогичным образом). Построение
выполняется для расширяющейся части
сопла, так как суживающаяся часть нами
не профилировалась, закон изменения
площади сечения для нее не определялся,
следовательно, нельзя определить закон
изменения параметров в ней. Для давления
известно лишь, что во входном сечении
оно равно
,
а в горле -
,
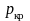а характер изменения давления между
этими сечениями – функция произвольно
нарисованного профиля суживающейся
части сопла.
После
выполнения основной части расчетного
задания известны безразмерные параметры
l,
t,
p,
e,
q,
M
в следующих сечениях: критическое
(индекс “кр”), выходное сечение в
расчетном режиме истечения (“1р”),
скачок уплотнения (параметры “1ск”
слева от скачка и “2ск” – справа),
выходное сечение в режиме течения со
скачком (“1”), выходное сечение в режиме
с выходным давлением
без скачка (“1т”). Размерные параметры
в этих сечениях могут быть определены
путем умножения безразмерных параметров
на соответствующий параметр торможения.
Например, для определения размерного
давления нужно безразмерный параметр
p
умножить на давление торможения, причем
для точек “кр”, “1р”, “1ск”, “1т”
нужно брать давление торможение
,
а для точек “1” и “2ск” – давление
торможения
.
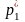4а. Точки на оси сопла, в которых будет рассчитывается давление
(нахождение
абсцисс
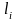графика
).
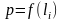Зная
площади сечений
,
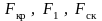можно определить, на каком расстоянии
от критического сечения (от горла сопла),
находятся эти сечения, сравнивая подобные
треугольники.
Расстояние от горла до скачка:
.
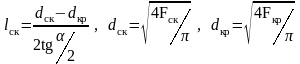(38)
Расстояние от горла до выходного сечения:
.
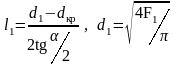(39)
Расстояние
от горла до выхода
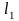делим на N=10-15
равных отрезков. Для каждого участка
определяем
:
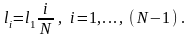(40)
Некоторые
из полученных сечений окажутся левее
скачка уплотнения (для них
),
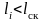другие будут правее (
).
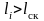4b.
Построение зависимости
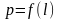
от критического сечения до скачка уплотнения.
Определяем давление в точках, абсциссы которых .
Находим
для каждой
диаметр
:
.
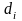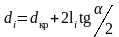(41)
В каждой i-ой точке вычисляем функцию тока по формуле, которая является аналогом формулы (30а):
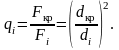(42)
По функции тока в таблицах газодинамических функций находим безразмерные параметры
.
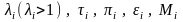Умножая безразмерную величину (в нашем
примере p)
на параметр торможения (левее скачка
давление торможения
),
получаем искомое значение давления
.
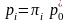4с. Построение зависимости
от скачка уплотнения до выходного сечения.
Определяем давление в точках, абсциссы которых .
Как и ранее, находим для каждой диаметр по (41).
В каждой i-ой точке вычисляем функцию тока по формуле, которая является аналогом формулы (32):
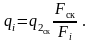(43)
По функции тока в таблицах газодинамических функций находим безразмерные параметры
.
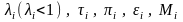Умножая p
на давление торможения, равное после
скачка уплотнения значению
,
получаем размерное давление
.
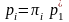Определив
давление
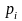во всех точках i=1…(N-1),
строим график зависимости
.
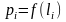На
график наносятся, помимо рассчитанных
значений
,
уже известные точки:
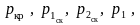а также отмечается значение
.