§1. Теплоємність ідеального газу

Якщо в результаті теплообміну тілу передається деяка кількість теплоти, то внутрішня енергія і температура тіла змінюються. Кількість теплоти Q, потрібна для нагрівання 1 кг речовини на 1 К називають питомою масовою теплоємністю речовини c, Дж/(кгК):

(1)

В інших варіантах зручно використовувати питому молярну теплоємність речовини с_{ ,} Дж/(кмольК):

(2)

або питому об’ємну теплоємність речовини , Дж/(м³К):

(3)

де  – молярна маса речовини.

За І законом термодинаміки зміна внутрішньої енергії тіла залежить не лише від отриманої кількості теплоти, а і від роботи, яку виконує тіло, тобто від характеру процесу. Така неоднозначність визначення теплоємності характерна лише для газоподібних речовин. При нагріванні рідин і твердих тіл їх об’єм практично не змінюється, і робота розширення дорівнює нулю. Тому вся кількість теплоти, отримана тілом, іде на зміну його внутрішньої енергії. На відміну від рідин і твердих тіл, газ у процесі теплообміну може значно змінювати свій об’єм і виконувати роботу. Внаслідок цього теплоємність газоподібної речовини залежить від характеру термодинамічного процесу. Розглядають два значення теплоємності газів: с_ – питому молярну теплоємність в ізохорному процесі (V = const) і с_p – питому молярну теплоєм-ність в ізобарному процесі (p = const).

Співвідношення, яке відображає зв’язок між питомими молярними теплоємностями с_ та с_{ p} має такий вигляд (формула Майєра):

, (4)

де R_ ─ універсальна газова стала, R_=8324 Дж/(кмольК) .

Враховуючи співвідношення (2) та (3), формулу Майєра можна записати в іншому вигляді:

; (5)

. (6)

Т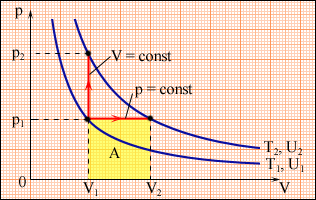 еплоємність газу в процесі з постійним тиском завжди більша теплоємності в процесі з постійним об’ємом (рис.1). При p = const газ додатково виконує роботу L = p₁(V₂ – V₁). Тому с_p > с_.

Рис.1. Ізобарний та ізохорний процеси нагрівання газу

Співвідношення теплоємностей у процесах з постійним тиском і постійним об’ємом називається показником адіабати, або коефіцієнтом Пуасона k:

(7)

Між двома ізотермами з температурами T₁ і T₂ на діаграмі (p, V) можливі різні шляхи переходу. Оскільки у всіх цих варіантах зміна температури ΔT = T₂ – T₁ однакова, відповідно буде однаковою зміна внутрішньої енергії ΔU. Однак виконана при цьому робота L і отримана в результаті теплообміну кількість теплоти Q будуть різними для різних шляхів переходу. Це означає, що газ має нескінченну кількість теплоємностей, а теплоємності с_p і с_ – це лише поодинокі варіанти.

При наближених розрахунках вважають, що теплоємність ідеального газу в інтервалі температур 0–150 С залежить не від температури газу, а лише від атомності газу – (кількості ступенів вільності), табл.2.

Таблиця 2

Гази	Питома молярна теплоємність у процесі		k
	ізохорному с  , кДж/(кмольК)	ізобарному с p , кДж/(кмольК)
Одноатомні	12,56	20,93	1,67
Двохатомні	20,93	29,31	1,4
Три- та багатоатомні	29,31	37,68	1,29