
- •Задание
- •Лабораторная работа № 2 Решение обратной задачи магниторазведки способом касательных
- •II. Гравиразведка
- •Лабораторная работа №1
- •Решение прямой задачи гравиразведки для некоторых тел
- •Простейшей формы
- •Порядок выполнения работы
- •Исходные данные
- •Формулы для вычисления аномального эффекта
- •Решение обратной задачи для вертикального пласта Теоретические сведения
- •3. Решение обратной задачи для вертикального уступа Теоретические сведения
- •Лабораторная работа № 3 Решение прямой задачи гравиразведки с использованием палетки Гамбурцева
- •Порядок пользования палетками
- •Список литературы
I. магниторазведка
Лабораторная работа № 1
Расчет элементов магнитного поля Земли
Цель работы: приобретение навыков при расчете элементов магнитного поля Земли.
Основы теории нормального магнитного поля Земли
Магнитное
поле нашей планеты в первом приближении
можно рассматривать как поле шара,
намагниченного по оси, отклоняющейся
от оси вращения приблизительно на 11,50.
Экспериментальные данные о напряженности
поля позволяют вычислить магнитный
момент Земли, который по современным
данным считается равным
![]() ед.СГС
(8,3.1022 А/м ). Напряженность
магнитного поля в каждой точке Земли
имеет определенное направление и
величину, т.е. является векторной
величиной. Вектор может быть представлен
составляющими по осям определенной
координатной системы. При определении
вектора геомагнитного поля за координатную
систему принимается прямоугольная
система координат; в таком измерении
плоскость XOY принимается
горизонтальной, ось X
направлена по географическому меридиану
на север, ось Y – по
параллели на восток, ось Z
– к центру Земли.
ед.СГС
(8,3.1022 А/м ). Напряженность
магнитного поля в каждой точке Земли
имеет определенное направление и
величину, т.е. является векторной
величиной. Вектор может быть представлен
составляющими по осям определенной
координатной системы. При определении
вектора геомагнитного поля за координатную
систему принимается прямоугольная
система координат; в таком измерении
плоскость XOY принимается
горизонтальной, ось X
направлена по географическому меридиану
на север, ось Y – по
параллели на восток, ось Z
– к центру Земли.
Н
Рис. 1. Элементы
геомагнитного поля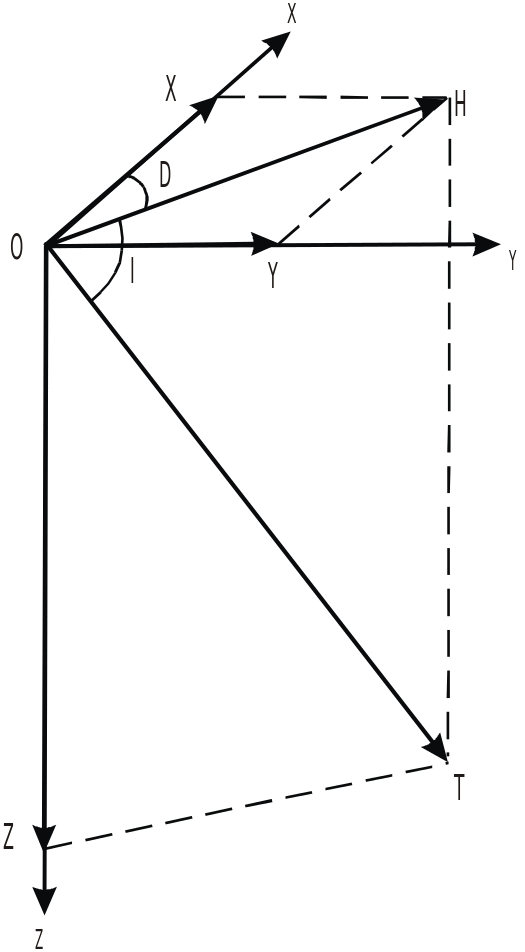
Между числовыми
значениями H, X,
Y существует
зависимость
![]() .
.
Вертикальная плоскость, в которой располагаются H и T, называется плоскостью магнитного меридиана, а линия сечения поверхности Земли с плоскостью магнитного меридиана – магнитным меридианом. Направление горизонтальной составляющей Н определяет положение магнитного меридиана в данной точке. Положение магнитного меридиана используется для определения магнитного азимута какого-либо направления. Магнитным азимутом называется угол между направлением магнитного меридиана в данной точке и заданным направлением, отсчет угла производится от направления магнитного меридиана по часовой стрелке. Магнитные меридианы сходятся в северном и южном магнитных полюсах (магнитные полюса – точки пересечения оси магнитного диполя с дневной поверхностью).
Угол между географическим и магнитным меридианами называется магнитным склонением D, а угол между направлением горизонтальной составляющей Н и направлением полного вектора напряженности магнитного поля Т или угол наклона Т к горизонту – наклонением J.
Склонение D, наклонение J, составляющие горизонтальная Н, вертикальная Z, северная X, восточная Y называются элементами земного магнетизма.
Элементы H, Z, X и Y измеряются в эрстедах (Э) в системе СГС или в ампер на метр в системе СИ (1Э) = [1/(4π)]·103 А/м=79,6 А/м, а D и J – в градусах.
При измерении слабых магнитных полей употребляется более дробная единица
![]() ,
т.е.
,
т.е.
![]()
Геомагнитное поле в первом приближении близко к полю однородно намагниченного шара или к полю диполя, помещенного в центр Земли.
Магнитный потенциал в любой точке наблюдения можно вычислить по формуле:
![]() ,
,
где
![]() – радиус Земли, равный
– радиус Земли, равный
![]() ,
,
![]() – магнитный момент, равный
– магнитный момент, равный
![]() ,
,
![]() – угол между осью земного магнитного
диполя и радиусом-вектором, проведенным
из центра Земли в данную точку на ее
поверхности. Магнитная широта, связанная
с географической широтой
– угол между осью земного магнитного
диполя и радиусом-вектором, проведенным
из центра Земли в данную точку на ее
поверхности. Магнитная широта, связанная
с географической широтой
![]() соотношением
соотношением
![]() .
.
Чтобы
найти вертикальную и горизонтальную
составляющие напряженности земного
магнитного поля Z и H
надо найти выражения соответствующих
производных магнитного потенциала в
принятой системе координат, когда
плоскость ХОУ касательная к
поверхности шара в точке наблюдения,
т.е. вычисляем производные по
![]() и
и
![]() .
.
Получим:
![]() ;
;
![]() (1)
(1)
Полный вектор T равен
![]() или
или
![]() (2)
(2)
направление его определяется углом наклона J
![]() (3)
(3)
Величина изменения напряженности поля в 1Тл, называется нормальным градиентом. Нормальный градиент вертикальной составляющей равен
![]() (4)
(4)
горизонтальной составляющей
![]() (5)
(5)
Выражения 1 – 5 дают общее представление об изменении элементов геомагнитного поля в зависимости от магнитной широты .
Полный вектор Т достигает наибольшего значения на полюсах, где =00, а наименьшего – на экваторе, при =900. Диапазон изменения Т от 2М/R3 до М/R3. Подставив значения М и R, получим, что напряженность Т изменяется от 0,66 до 0,33 Э (Эрстед). Вертикальная составляющая Z изменяется от 0,66 Э на полюсах до нуля на экваторе, а горизонтальная H – от нуля на полюсах до 0,33 Э на экваторе.
Задание
Вычислить значение потенциала
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и построить графики изменения их на
поверхности Земли. Угол
изменяется от
и построить графики изменения их на
поверхности Земли. Угол
изменяется от
![]() до
до
![]() с шагом
с шагом
![]()
Порядок выполнения работы
Записать условие, задание и необходимые формулы с кратким их пояснением.
Вычисляются
 ,
,
,
,
и полученные значения представляются
в виде таблицы
,
,
,
,
и полученные значения представляются
в виде таблицы
На миллиметровой бумаге в произвольном масштабе строятся графики изменения элементов геомагнитного поля в зависимости от магнитной широты (ось х).
По результатам работы делаются краткие выводы.
Лабораторная работа № 2 Решение обратной задачи магниторазведки способом касательных
Цель работы: Приобретение навыков в определении глубины залегания и намагниченности аномального тела.
Обратная задача магниторазведки заключается в вычислении по заданному распределению аномального поля параметров тела: глубины залегания, размеров, намагниченности и т. д. В общем случае решение обратной задачи неоднозначно.
При интерпретации необходимо опираться на полный и всесторонний анализ всех имеющихся геологических данных по району исследований. Такой анализ позволяет составить наиболее вероятную схему геологического строения. При решении обратной задачи часто делают допущение о правильной форме тела, создающего аномалию. Для таких тел можно найти аналитическое выражение, связывающее параметры тела со значением аномалии в некоторых характерных точках.
Широкое распространение, особенно при интерпретации данных магниторазведки, получил способ касательных. Этот способ был предложен Ю. Н. Грачевым для определения глубины залегания верхней кромки возмущающих тел по резко аномальным кривым ∆ или ∆Т. В общем виде формулу метода касательных можно записать так
h = К (Х2 – Х1), где
h – глубина залегания верхней кромки магнитоактивных масс,
(Х2 – Х1) – разность абсцисс пересечения касательных к исходной кривой в точке максимума и перегиба,
К – коэффициент, определяемый формой тела.
В.К. Пятницкий, изучив ряд теоретически рассчитанных аномалий, оценил величины возможной погрешности определения h и предложил вводить поправочные коэффициенты, учитывающие форму тела. Им исследованы аномалии, обусловленные пластами и уступами.
При интерпретации аномалии от пластообразных тел он рекомендует вычислять отношение
![]() (6)
(6)
и по нему, используя график (рис. 2), определяем коэффициенты
![]() ;
;
![]() ;
;
![]() .
.
Глубина может быть определена
![]() (7)
(7)
![]() (8)
(8)
Хm – абсцисса пересечения касательных к точке перегиба и точке максимума (рис. 3).
Х0 – абсцисса пересечения касательной с осью х.
Хп – абсцисса точки перегиба.
Мощность пласта оценивается формулой
2b = 2Кh (9)
b – полумощность пласта..
Намагниченность равна
![]() (10)
(10)
Та мах – максимальное значение аномального магнитного поля.
Глубину залегания нижней кромки магнитоактивных масс Н можно определить по формуле Булиной
Н = 2 Хmin – 1,8 (b + h) (11)
Хmin – абсцисса точки минимума
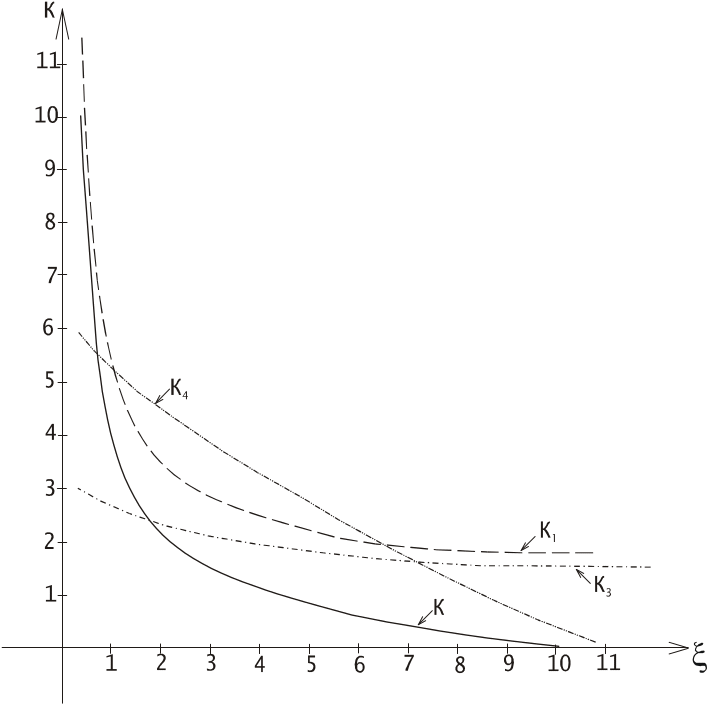 Рис.
2. Определение
коэффициентов
Рис.
2. Определение
коэффициентов
Порядок выполнения работы
1. С карты изодинам, выданной преподавателем, вкрест простирания аномалии снять значения изолиний и по ним построить график Та.
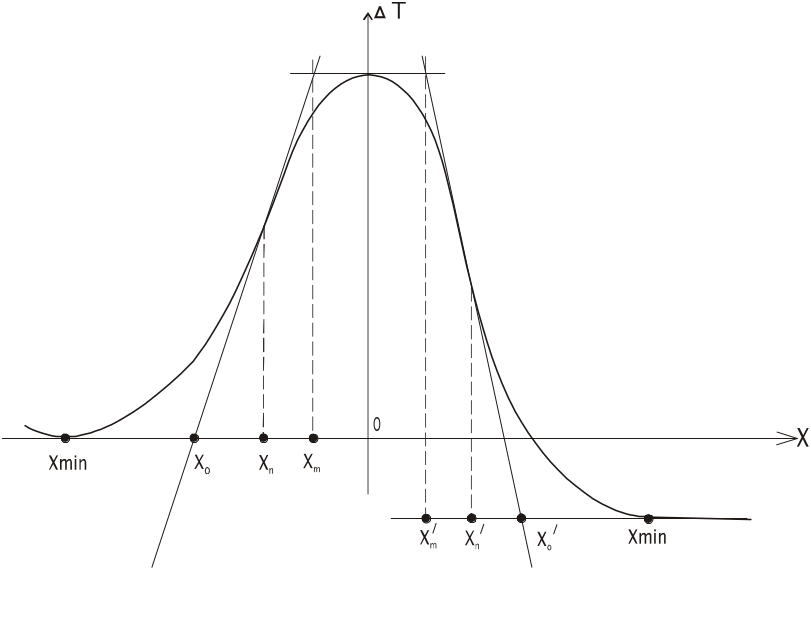 Рис.
3. Характерные точки по методу касательных
Рис.
3. Характерные точки по методу касательных
2. а) За начало координат принимается положение точки максимума Та,
б) к интерпретируемой кривой проводят касательные к точкам перегиба, максимума, минимума,
в) выделяются характерные точки,
г) определяются абсциссы Хn, Х0, Хm .
3. По формуле (6) определяется входной параметр ξ , используя который, с графика снимают значение коэффициентов К, К1, К3, К4. По формулам (7) и (8) определяют h, по формуле (9) вычисляют значение 2b, по формуле (10) – I, по формуле (11) - Н.
4. Расчеты производятся по обеим ветвям кривой Та. На миллиметровке изображается график Та и полученные размеры тела.
