47. Напряженные состояния в точках тела . Главные площадки и главные напряжения . Виды напряженного состояния.

Материалы находящиеся под растяжением – сжатием над 2 –м или трем осям системы координат , имеет место сложное напряженное состояние .

При исследовании растяжений тела , напряженность состояния описывалась 2-мя видами напряжений .

Установили различные соотношения этих растяжений , которые зависят от угла наклона площади поперечного сечения.

Площадки ,на которых касательные напряжения =0, называются главными , а напряжения на этих площадках главными напряжениями.

Согласно точной теории упругости для общего случая напряженного состояния в точке, имеет место 3-и главных взаимноперпендик-ных площадки, через которые передаются главные напряжения.

Главные напряжения σ₁ > σ₂ > σ₃

Существует 3 –и вида напряженных состояния :

1) σ₁≠ 0, σ_2,3=0

Осевое простое напряженное состояние (при растяжении)

2) σ_1,2≠ 0, σ₃=0

Плоское напряженное состояние

3) σ_1,2,3≠ 0Объемное ,напряженное состояние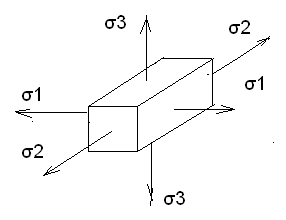

48. Деформация бруса при объемном ,напряженном состоянии. Обобщенный закон Гука.

Рассматривается элементарный объем вокруг какой либо точки тела, при исследовании прочности в данной точке необходимо знать не только главное напряжение σ_1,2,3, но и деформацию в этой точке.

Изменение формы тела всегда связано с перемещением этих точек тела.

Рассмотрим деформацию по осям

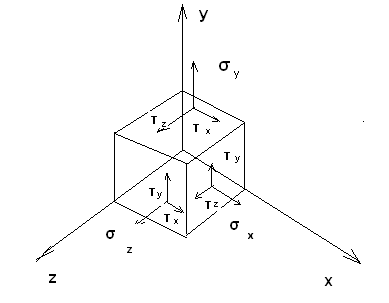
ε_x = σ₁/E - μ σ₂/E - μ σ₃/E

ε_y = σ₂/E - μ σ₁/E - μ σ₃/E (1)(все уравнения)

ε_z = σ₃/E - μ σ₁/E - μ σ₂/E

Аналитическое выражение закона Гука.

Исследование (1) приводит к зависимости объемной деформации и главных напряжений. Сумма слева – относительная объемная деф-я.

Относительное изменение объема

e = ε_x+ ε_y+ ε_z

V₀ = 1

V = (1+ ε_x)* (1+ ε_y)* (1+ ε_z)

V = 1 + ε_x+ ε_y+ ε_z

Используется для сложного напряженного состояния.

49. Теории (гипотезы) прочности и их назначение . Понятие о эквивалентных напряжениях . Содержание и области применения теории прочности.

Теории предельных напряжений .Гипотезы прочности.

Задачи теории прочности:

Оценить прочность детали находящейся в сложном напряженном состоянии через хорошо известное простое напряженное состояние.

В каждой теории используются свои критерии расчета.

1) Теория наибольших нормальных напряжений.

Если в какой –либо точке тела, в каком –либо направление нормальное напряжение достигает МАХ значение- происходит разрушения.(простые конструкции, сложные материалы)

Галлелеу σ_мах<=[ σ]

2) Теория наибольших линейных деформаций

Разрушение материалов рассматривают с точки зрения молекулярной теории. Происходит разрушение молекулярных сил, изменяется расстояние между молекулами.

Разрушение в каждой точке произойдет если критические деформации будут близки к предельным.

ε<= [ε] σ₁ - μ σ₂ - μ σ₃ <= [σ] σ_экв<=[ σ]

Эквивалентное напряжение – напряжение, которое необходимо создать в растянутом стержне, чтобы его простейшее состояние было равно опасному сложному состоянию напряженного тела.

(твердые материалы, расчет простых деталей)

3) Теория наибольших касательных напряжений

Пластические деформации , которые в какой –либо точке достигнут произойдет разрушение.

Условие прочности

τ_max <=[ τ]

σ₁ - σ₃ <= [σ]

Для плоско напряженного состояния получена зависимость

σ_экв= √( σ² + 4 τ²)<=[ σ]

4) Энергетическая теория прочности

Согласно этой теории на разрушение материала затрачивается не вся потенциальная энергия, а только часть , идущая на формообразование тела.

U_ф<= [U_ф]

Для плосконапряженного состояния получена зависимость.

Используется при статических расчетах на прочность . Для пластичных материалов.

5) Теория Мора

Согласно этой теории единого критерия оценки прочности при различных напряженных состояниях нет. Разрушение материала зависит от величины и знака наибольшего и наименьшего главных напряжений.

Условие прочности

σ₁ – k*σ₃ <= [σ]

k – коэф-т учитывающий разные свойства материала при напряжение сжатии.

K = [ σ_р]/ [ σ_с]