1. Виды нагружения. Напряжение, основные понятия. Реальный объект.

Если в поперечных сечения бруса возникает только нормальная силаN, то брус растянут (сила N направлена от сечения) или сжат (сила N направлена к сечению). Если в поперечном сечении возникает только момент Mz, то брус в данном сечении работает на кручение. Если в поперечном сечении возникает только изгибающий момент Mx или My, то происходит чистый изгиб. Если в поперечном сечении наряду с изгибающим моментом возникает и поперечная сила Qx или Qy, то это поперечный изгиб (сдвиг, срез).

2.Напряжение – это численная мера распределения внутренних сил по плоскости поперечного сечения. Использ-ся при исследовании внутрен. сил конструкций. Единицей напряжения служит единица силы, делённая на единицу площади – 1Н/м²=1Па.

Рассмотрим брус, к которому приложена некоторая нагрузка. Применяя метод сечения, рассечем брус некоторой попереч. плоскостью отбросим левую часть бруса и рсссмотрим равновесие оставшейся правой части. Площадь сечения - ∆S. На этой площадке действует равнодействующая внутренних сил - ∆R.

P_ср=∆R/∆S – среднее напряжение. Числовое значение полного напряжения Р = lim∆R/∆S.

- полное напряжение, где σ – нормальное напряжение, τ – касательное напряжение.

- если Р – пространствен. вектор.

Наличие нормального напряжения в любой точке поперечного сечения обусловлено возникновением в этом сечении нормальной силы N или изгиб. моментов Mx и My. Наличие касательных напряжений обусловлено внутренними силовыми факторами, возникающими в плоскости сечения, т. е. поперечными силами Qy, Qx или крутящим моментом Mz. Если нормальн. или касат. напряжения превышают предельные значения, то происходит разрушение конструкции.

П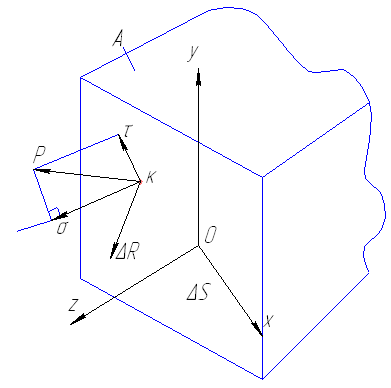редельное состояние – это состояние разрушенной детали, которой нельзя пользоваться. Деформация – когда деталь изменяет линейные размеры и больше не возвращается в начальное состояние.

Брус- это геом-ое тело, одно из измерений которого много больше 2-х других

Оболочка – это геом-ое тело, одно из измерений которого много меньше 2-х других.

3. Напряжение и деформированное состояние, свойства (характеристики) материала.

Напряжённое состояние – совокупность напряжений во множестве площадок, проходящих через заданную точку тела, образуют напряж. состояние.

Деформированное состояние – совокупность линейной и угловой деформации во множестве площадок, проходящих через заданную точку тела.

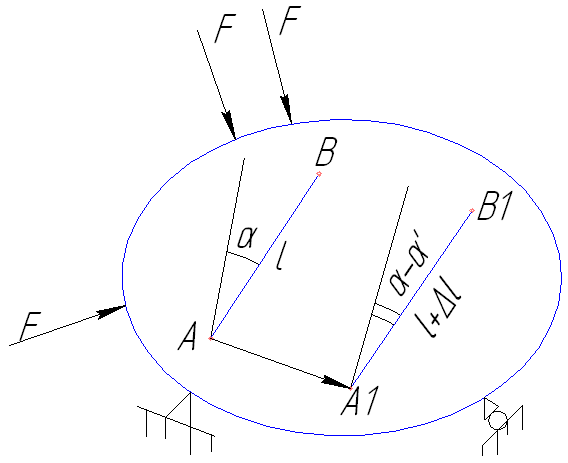
Рассмотрим тело, на которое действует сис-ма сил. Рассмотрим в этом теле отрезок АВ:

L – длина до деформации;

А1В1 – отрезок после деформации;

L+∆L – длина после деформации;

∆L – абсолютное удлинение отрезка;

АА1 – вектор полного перемещения;

α – α’ – угловая деформация.

Ε = ∆L/L – относительная деформация (при Ε>=15%, то данный материал можно штамповать).

Вывод: основным видом расчёта на прочность явл-ся расчёт по напряжениям; а расчёт на жесткость ведётся по определению деформации.

Механич. св-ва материала:

- Прочность – способность не разрушаться под нагрузкой;

- Жёсткость – способность незначительно деформироваться под нагрузкой;

- Выносливость – способность долгое время выдерживать переменные нагрузки;

- Устойчивость – способность сохранять первоначальную форму упругого равновесия;

- Вязкость – способность воспринимать ударные нагрузки.

Характеристики материалов:

- Твёрдость;

- Хрупкость;

- Пластичность.

Допущения о свойствах материалов:

Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;

Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;

Изотропны – механич. св-ва не зависят от направления нагружения;

Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.

4.Метод сечения, виды внутренних силовых факторов.

Для выявления внутренних сил в сопротивлении материалов применяется метод сечения.

Суть метода: рассекаем тело плоскостью; мысленно отбрасываем наиболее нагруженную часть тела (1); действие отброшенной части тела на оставшейся части замещаем равнодействующими внутренних силовых факторов и приводим их в центр тяжести поперечного сечения. Поперечное сечение – это сечение, плоскость которого перпендикулярна оси тела. Главные векторы сил эквивалентны действию отброшенной части на оставшуюся часть. При этом оставшаяся часть тела нах-ся в равновесии. Ур-ние равновесия: .

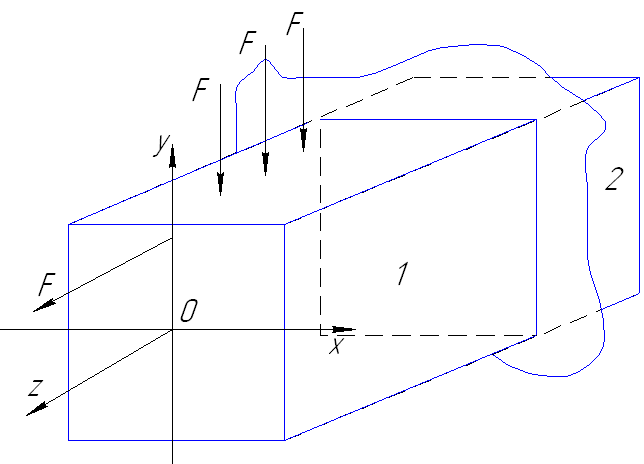
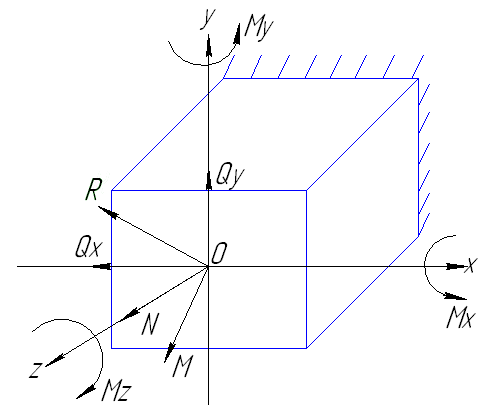
Разложив главный вектор R и главный момент M на составляющие по осям, получим силы N, Qx, Qy, и моменты Mx, My, Mz, которые называются внутренними силовыми факторами. Шесть внутр.силовых факторов вместе с известными внеш.силами на оставшейся части тела образуют уравновешенную сис-му сил, для кот. можно составить 6 ур-ний равновесия.

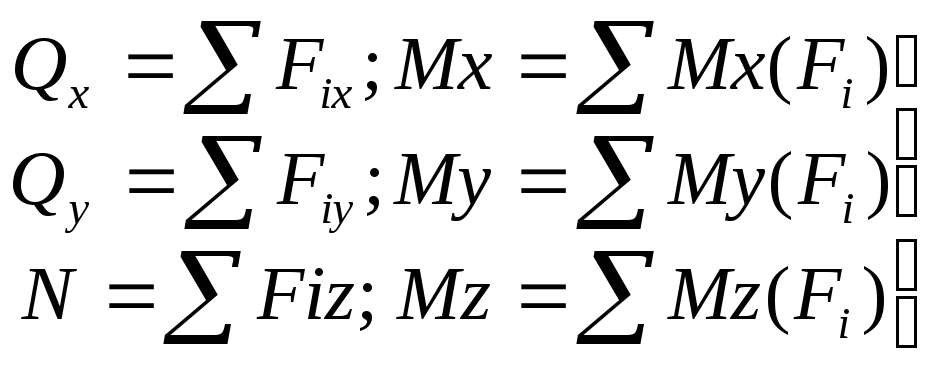
N – нормальная (продольная) сила;

Qx, Qy – поперечные силы;

Mz – крутящий момент;

Mx, My – изгибающие моменты.

5.Растяжение. Основные понятия, допущения и зависимости.

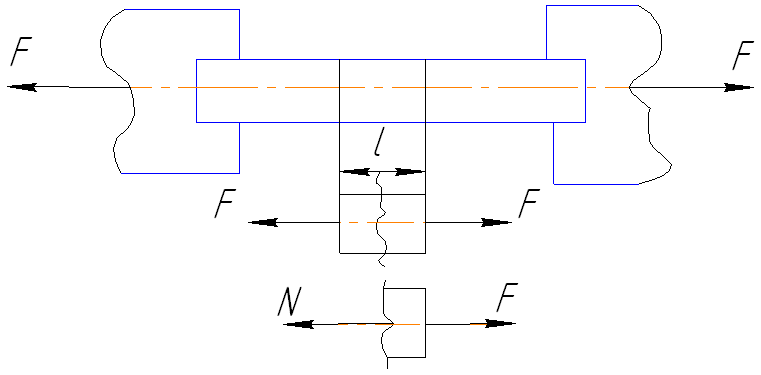
Растяжение – это такой вид нагружения, когда в поперечном сечении растянутого тела действуют только продольные силы N. Прямой брус, работающий на растяжение, наз-ся стержнем.

Согласно методу сечений рассечём растянутый стержень и отбросим его левую часть, то для уравновешивания внешней силы F (равнодействующая сис-ма сил крепления образца) достаточно в сечении приложить только один внутренний силовой фактор – нормальную силу N.

N=F – условие равновесия. Остальные внутренние силовые факторы в данном случае равны 0. При растяжении стержень нах-ся в напряжённом состоянии. Напряжение при растяжении σ=N/S, где S – площадь поперечного сечения. Нормальное напряжение направлено также как и нормальная сила.

Ряд допущений:

- по всей длине участка действ. внутр. сила;

- внутр. сила по попереч. сечению распределена равномерно;

- по всей длине участка l значение деформации ∆ l и Е постоянны.

Если в рез-те алгебраич-го сложения проекций внешних сил получилось, что N>0, то нормальная сила направлена от сечения и стержень в этом сечении испытывает растяжение; иначе стержень испытывает сжатие.

Если стержень нагружен большим числом осевых сил направленных в противоположные стороны, то применяется правило знаков при определении нормальной силы: проекции внешних сил, направленных от сечения, положительны и, наоборот.

При переходе от одного сечения к другому нормальная сила изменяется, поэтому строят графики изменения значения нормальной силы N по длине бруса, кот. наз-ся эпюрами.