
- •3. Напряжение и деформированное состояние, свойства (характеристики) материала.
- •4.Метод сечения, виды внутренних силовых факторов.
- •5.Растяжение. Основные понятия, допущения и зависимости.
- •6.Растяжение, закон Гука. Основные понятия и зависимости, влияние на абсолютное удлинение стержня.
- •7.Механические хар-ки. Диаграмма растяжения.
- •8.Деформация при растяжении (продольные, поперечные, коэф-т Пуассона).
- •9.Растяжение. Напряжение на наклонной поверхности стержня.
- •10.Кручение, основные понятия, обозначение, правило знаков.
- •11.Изгиб. Основные понятия (допущения, чистый, поперечный). Виды опор.
- •12.Изгиб. Напряжение и деформация.
- •13. Изгиб. Правило Верещагина.
- •14. Сдвиг. Основные понятия, напряжения, зависимости, закон парности. Расчет на срез.
- •15. Обобщенный закон Гука. Деформация при плоском и объемном напряжении состояния.
- •16.Изменение объема при объемном напряженном состоянии. Обобщенный закон Гука.
- •17.Теории предельных состояний. Общие понятия и назначение. 1,2,3 теории.
- •18. Теории предельных состояний. Общие понятия и назначение. 4,5 теории.
- •19. Сложное сопротивление. Общие понятия, назначение. Косой изгиб. Изгиб и растяжение
- •20.Косой изгиб
- •21.Изгиб и растяжение (сжатие)
- •22. Сложное сопротивление. Общие понятия, назначение. Косой изгиб. Изгиб с кручением
- •23. Усталостная прочность. Общие понятия, назначение. Параметры циклов нагружения
- •24. Усталостная прочность. Общие понятия, назначение. Предел выносливости при симметричном цикле
- •25. Усталость. Факторы, влияющие на предел усталости. Общие понятия, назначение
- •26. Усталость. Общие понятия, назначение. Расчет на прочность при переменных напряжениях
- •27. Реальный объект и его схема. Схематизация свойства материала, формы элементов конструкций нагрузок
- •28. Внешние и внутренние силы. Применение метода сечения для определения внутренних сил и напряжений
- •29. Понятие о напряжениях, деформациях и перемещениях. Нормальные и касательные напряжения. Вектор полного перемещения. Линейная и угловая деформация
- •30. Растяжение и сжатие. Определение внутренних сил. Натяжение в попересных и наклонных сечениях.
- •31) Продольная и поперечная деформация при растяжении и сжатии. Коэффициент Пуассона. Закон Гука при растяжении. Потенциальная энергия деформации.
- •32. Экспериментальное изучение свойств материалов при растяжении и сжатии. Диаграмма растяжения. Основные характеристики материалов (механические).
- •33. Расчёт на прочность при растяжении и сжатии. Допускаемое напряжение и коэффициент запаса.
- •34. Чистый сдвиг. Напряжение и деформация при сдвиге.
- •35. Кручение бруса круглого, поперечного сечения. Напряжение и деформация при кручении. Определение максимальных касательных напряжений.
- •36. Геометрические характеристики брусьев круглого, поперечного сечения при кручении. Потенциальная энергия деформации при кручении.
- •11) Расчёт валов на прочность и жёсткость при кручении.
- •37. Моменты инерции сечения. Вычисление моментов инерции брусьев прямоугольного и круглого сечения.
- •38.Прямоугольное сечение.
- •39.Круглое сечение
- •40. Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры. Дифференциальные зависимости при изгибе.
- •41. Примеры элементов конструкций, работающих на изгиб. Типы опор и определение опорных реакций.
- •42. Расчет на прочность при изгибе
- •43. Напряжение в брусе при поперечном изгибе
- •44. Аналитический метод определения перемещений в балке при изгибе. Дифференциальное уравнение упругой линии. Вычисление прогибов и углов поворотов сечений.
- •45. Потенциальная энергия бруса в общем случае нагружения.
- •46. Определение перемещения бруса способом Верещагина
- •47. Напряженные состояния в точках тела . Главные площадки и главные напряжения . Виды напряженного состояния.
- •48. Деформация бруса при объемном ,напряженном состоянии. Обобщенный закон Гука.
- •49. Теории (гипотезы) прочности и их назначение . Понятие о эквивалентных напряжениях . Содержание и области применения теории прочности.
- •50. Сложное сопротивление бруса. Расчеты на прочность при косом изгибе.
- •51. Понятие об усталостной прочности. Основные характеристики цикла переменных напряжений.
- •52. Прочность при перемещенных напряжениях.
- •53.Влияние концентраций напряжений, состояния поверхности и размеров детали на усталостную прочность
- •54. Расчет на прочность при переменных напряжениях.
- •55. Местные напряжения. Концентрация напряжения
- •56. Контактные напряжения. Формула Герца
- •57.Устойчивость.
41. Примеры элементов конструкций, работающих на изгиб. Типы опор и определение опорных реакций.
Конструкции опор:
а) Шарнирно – неподвижная опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).
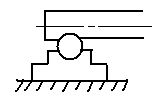

б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки.
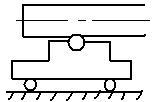
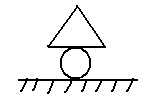
в) Консольная опора – жёстко замоналиченая консоль.

Реакции в опорах определяют из условия равновесия (уравнение статики).
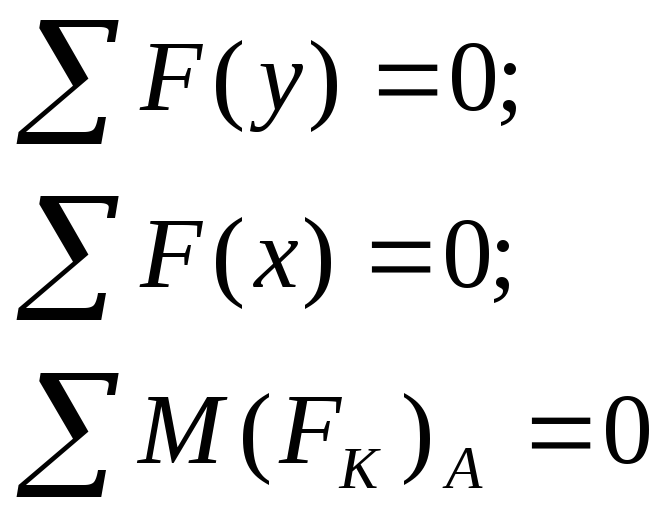
42. Расчет на прочность при изгибе
Под изгибом понимается такой вид нагружения , при котором в поперечных сечениях бруса возникают изгибающие моменты. Большей частью , в поперечных сечениях бруса наряду с изгибающими моментами возникают так же и поперечные силы, в этом случае изгиб называется поперечным.
При изгибе балки происходит искривление ее оси в плоскости действия внешней силы.
Y″= 1/ρ = Mu/EJz
Y - перемещение сечения балки.
1/ρ – кривизна . E – модуль упругости 1 –го рода .
Jz – экваториальный момент инерции сечения балки относительно оси z.
Величина EJz называется жесткостью бруса при изгибе.
Исключая кривизну из предыдущей формулы получим выражение для напряжения:
σ = Muy/Jz
Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии
σmax = Muy max/Jz
Отношение Jz/ymax называется моментом сопротивления сечения при изгибе и обозначается через Wх :
Wх = Jz/ymax
Таким образом,
σmax = Mu/ Wх
Эта формула является основной при расчете на прочность бруса при изгибе.
Для бруса прямоугольного сечения Jz = bh3/12
Для бруса круглого сечения Jz = πD4/64
43. Напряжение в брусе при поперечном изгибе
В случае поперечного изгиба в сечение бруса возникает не только изгибающий момент , но и поперечная сила Q. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения . Следовательно , в этом случае в поперечных сечениях бруса возникают не только нормальные , но и касательные напряжения.
Касательные напряжения τ сопровождаются появлением угловых деформаций γ.
τ = G* γ
G – модуль упругости 2-го рода.
Поэтому , кроме основных смещений , свойственных чистому изгибу , получаются некоторые дополнительные угловые смещения, обусловленные сдвигом.
При поперечном изгибе в отличие от чистого изгиба поперечные сечения бруса не остаются плоскими, они искривляются.
Однако на величине нормальных напряжений искажение плоскости поперечных сечений заметным образом не скажутся.(Поперечная сила Q не меняется по длине бруса)
Формулы для чистого изгиба , будут давать совершенно точные результаты и в случае поперечного изгиба.
σ = Muy/Jz
Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии
σmax = Muy max/Jz
Отношение Jz/ymax называется моментом сопротивления сечения при изгибе и обозначается через Wх : Wх = Jz/ymax
Таким образом,
σmax = Mu/ Wх
Эта формула является основной при расчете на прочность бруса при поперечном изгибе.
Для бруса прямоугольного сечения Jz = bh3/12
Для бруса круглого сечения Jz = πD4/64
Формулы для чистого изгиба дают некоторую погрешность h/l по сравнению с единицей,
Где h – размер поперечного сечения в плоскости изгиба,
L - длина бруса
