
- •1 Составление вариантов
- •1.1 Составление первого варианта
- •1.2 Проектирование второго варианта
- •1.3 Составление и подсчет стоимости третьего варианта
- •1.4 Анализ вариантов и выбор решения
- •2 Расчет плиты проезжей части Нагрузки а14 и нк14
- •2.1 Определение расчетных значений внутренних усилий
- •2.1.1 Определение нормативных значений постоянных и временных нагрузок
- •2.1.2 Определение расчетных значений внутренних усилий
- •Назначение размеров расчетных сечений
- •Расчет сечений плиты по прочности
- •2.4 Расчет сечений плиты на выносливость
- •Расчет нормального сечения плиты на трещиностойкости
- •3 Расчет главной балки
- •3.1 Расчетные положения
- •3.2 Расчет внутренних усилий по мкэ в программно-вычислительном комплексе midas Civil
- •3.2.1 Внутренние усилия
- •Поэтапные проверки характерных сечений
- •Расчет промежуточной опоры моста
- •4.1 Сбор нагрузок
- •4.2 Расчет сжатой стойки по устойчивости формы и прочности
- •4.3 Расчет внецентренно-сжатого сечения по трещиностойкости
- •4.4 Расчет ригеля опоры по прочности на местное сжатие
- •Конструирование
- •Приложения
Поэтапные проверки характерных сечений
Расчет нормального сечения в четверти крайнего пролета
Этап 1 Определение количества и мест расположения арматуры
В ¼ крайнего пролета возникают большие
усилия, чем в ½ крайнего пролета. Зададим
расчетную схему: Аh1
-
площадь вута сопряжения рёбер и плиты
верхнего пояса с радиусом R1=300
соответственно,
определяемые по формулам:
¼ крайнего пролета возникают большие
усилия, чем в ½ крайнего пролета. Зададим
расчетную схему: Аh1
-
площадь вута сопряжения рёбер и плиты
верхнего пояса с радиусом R1=300
соответственно,
определяемые по формулам:
П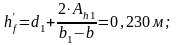 риведенная
толщина верхней плиты с учётом вутов:
риведенная
толщина верхней плиты с учётом вутов:
По тем же формулам определим толщину нижней полки двутавра, полученное сечение двутавра на рисунке3.3:
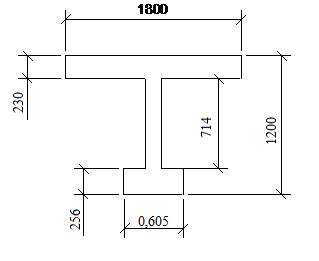
Рисунок 3.3 – Расчетное сечение в пролете
В расчете по прочности приняты допущения, что арматура и бетон достигли пределов условной текучести и прочности соответственно.
Определим требуемую площадь Артреб из условия, что внешний момент воспринимается нижней преднапряженной арматурой.
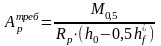
где
M0,5=
4174
кН∙м; Rp
= 1055МПа – расчетное сопротивление
арматуры; h0
= h
– 0,1
= 1,2 – 0,1 = 1,1 м;
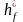 = 0,23м.
= 0,23м.
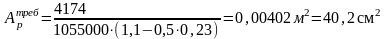
Количество пучков проволоки:
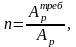
Ар = 9,42 см2.
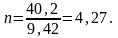
Принимаем 5 пучков по 48 проволок В-1400 диаметром 5 мм.
Фактическая площадь арматуры:
Арфактич = п∙Ар,
Арфактич = 5∙9,42 = 47,1см2.
Арматура в сжатой зоне принимается конструктивно
А/р > 0,1Ар = 0,1*47,1 см2 =4,71 см2.
Принимаем 2 пучка по 24 проволоки В-II диаметром 5 мм.
Арфактич =2∙4,71=9,42 см2.
Центр тяжести
сжатой арматуры расположен на расстоянии
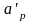 от внешней грани сжатой зоны:
от внешней грани сжатой зоны:
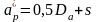 ,
,
где
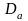 - диаметр анкера,
=
128 мм, s – защитный
слой бетона, s =
4 см.
- диаметр анкера,
=
128 мм, s – защитный
слой бетона, s =
4 см.
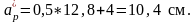
Центр тяжести сжатой арматуры:

Центр тяжести растянутой арматуры:


Рисунок 3.4 – Расположение напрягаемой арматуры
Предполагаем, что граница сжатой зоны проходит в плите, тогда
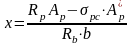 ,
,
где
σрс
– остаточное напряжение в верхней
арматуре, оставшееся непогашенным к
моменту разрушения, МПа;
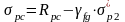 ;
;
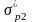 -
напряжение арматуры с учетом всех потерь
(
=0,8Rp=0,8∙1055
= 844 МПа);
-
напряжение арматуры с учетом всех потерь
(
=0,8Rp=0,8∙1055
= 844 МПа);
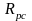 -
используемое в расчетах по прочности
наибольшее сжимающее напряжение в
арматуре, расположенной в сжатой зоне
и имеющей сцепление с бетоном, МПа,
-
используемое в расчетах по прочности
наибольшее сжимающее напряжение в
арматуре, расположенной в сжатой зоне
и имеющей сцепление с бетоном, МПа,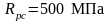 ;
;
γfg – коэффициент надежности, γfg = 1,1;
 -
сопротивление бетона осевому сжатию.
-
сопротивление бетона осевому сжатию.
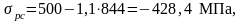
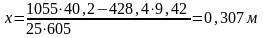
Проверка выполнения условия:

где значение y - высота сжатой зоны, при которой предельное состояние бетона сжатой зоны наступает не ранее достижения в растянутой арматуре напряжения, равного расчетному сопротивлению Rр :
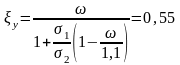 ;
;
= 0,85 - 0,008 Rb = 0,85 - 0,008*25 = 0,65
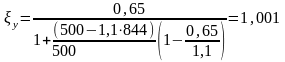
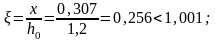
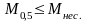 ,
,
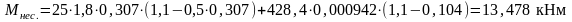
4174 кН∙м < 13478кН∙м. Условие выполняется.
Этап 2 Геометрические характеристики сечения
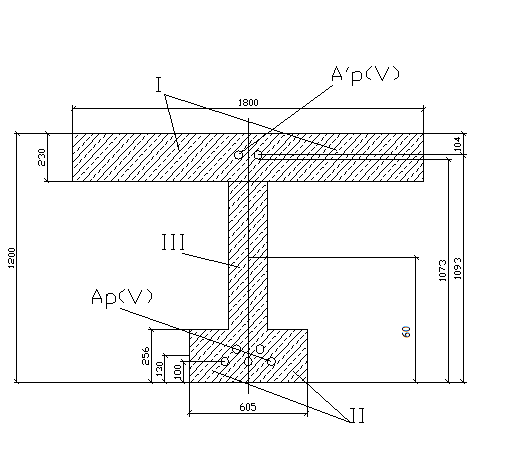
Рисунок 3.5 – Схема к определению геометрических характеристик в балке
Подсчет геометрических характеристик производился в табличной форме с помощью программы EXCEL.
При натяжении арматуры на бетон геометрические характеристики подсчитывают два раза:
1.для сечения с пустыми продольными каналами (без преднапряжения арматуры и заполнения бетона);
2.для сечения с заполненными раствором каналами и преднапряженной арматурой.
1.C пустыми продольными каналами:
Элемент |
А(м²) |
у(м) |
S (м³) |
Ia-a (м) |
Ic |
I |
0,176 |
1,073 |
0,1888 |
0,202634 |
0,0018 |
II |
0,176 |
0,13 |
0,0229 |
0,002974 |
0,0008 |
III |
0,214 |
0,6 |
0,1284 |
0,07704 |
0,0005 |
IV |
0,018 |
0,097 |
0,002 |
0,000198 |
|
V |
0,004 |
1,093 |
0,0044 |
0,004779 |
|
Сумма |
0,624 |
|
0,3465 |
0,287624 |
0,0031 |
АIV = (np – 1)∙Ap, АV = (np – 1)∙A/p
где пр – отношение модулей упругости бетона и арматуры,
пр = Ep/Eb = 2∙105/36∙103 = 5,56
АIV = (5,56– 1)∙0,00402= 0,0183м2,
АIV = (5,56 – 1)∙0,000942 = 0,0043 м2.
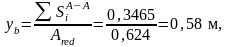
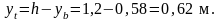
Момент инерции сечения:
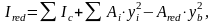

2.С заполненными раствором каналами:
Элемент |
А(м²) |
у(м) |
S (м³) |
Ia-a (м) |
Ic |
I |
0,176 |
1,073 |
0,1888 |
0,2026 |
0,0018 |
II |
0,176 |
0,13 |
0,0229 |
0,003 |
0,0008 |
III |
0,214 |
0,097 |
0,0208 |
0,002 |
0,005 |
IV |
0,018 |
0,097 |
0,002 |
0,0002 |
|
V |
0,004 |
1,093 |
0,0044 |
0,0048 |
|
Сумма |
0,624 |
2,49 |
0,2389 |
0,2126 |
0,0076 |

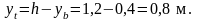
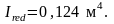
Этап 3 Назначение контролируемого напряжения
Величина контролируемых напряжений арматуры сжатой зоны приравнена к расчетному сопротивлению, а растянутой арматуры равна ее максимальному значению для проволочной арматуры.
При этом целесообразно сразу создать предварительное напряжение.
Np,con – контролируемая величина усилия в арматуре,
Np,con = σp,con∙Ap.
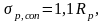
где Rp – расчетное сопротивление предварительно напряженной арматуры.
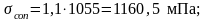
Np,con
= 1160,5∙0,00402=4,66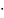 106
Н
106
Н
Подсчет потерь напряжений:
потери в стадии изготовления:

где
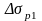 - потери напряжений первой группы.
- потери напряжений первой группы.
При натяжении ПНА на бетон:
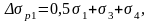
потери в стадии эксплуатации:
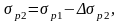
где
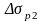 - потери напряжений второй группы.
- потери напряжений второй группы.
При натяжении на бетон:
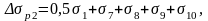
Виды потерь:
σ1 – потери от релаксации напряжений в натягиваемой арматуре,



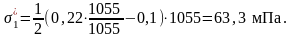
σ3 – потери от деформации анкеров, расположенных у натяжных устройств;
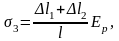
где Δl1 – обжатие шайб под анкерами и обмятие бетона под шайбами, равно 0,5 мм на каждый шов, но не менее 2 мм на каждый анкер, за который производится натяжение;
Δl2 – деформация арматурного элемента относительно анкера, принимаемая равной для конусного закрепления 2 мм на анкер;
l – длина натягиваемого элемента, l = 63000 мм;
Ер – модуль упругости натягиваемой арматуры, Ер = 2∙105 МПа.
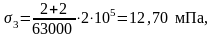
σ4 – потери от трения арматуры
а) о стенки закрытых и открытых каналов при натяжении арматуры на бетон
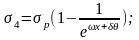
где е – основание натурального логарифма;
ω, δ – коэффициенты, определяемые по табл. 2 /1/, ω = 0,005, δ = 0,55;
x – длина участка от натяжного устройства до расчетного сечения, x =29 м,
θ - суммарный угол поворота оси арматуры, 0 рад
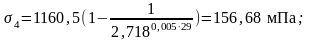

б) об огибающие приспособления не учитываем.
Определим потери напряжения первой группы:
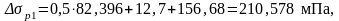
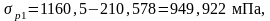
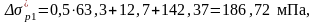
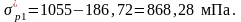
σ7 – потери от усадки бетона при натяжении:
при натяжении на бетон независимо от условий твердения при классе бетона В50 σ7 = 35МПа;
σ8 – потери от ползучести бетона:
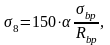 при
при
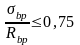 и
и
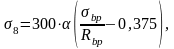 при
при
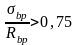 ,
,
где σbp (или σ/bp) – напряжения в бетоне на уровне центра тяжести арматуры Аp и А/р соответственно с учетом потерь напряжений в арматуре (см. этап 4);
Rbp – передаточная прочность бетона в момент передачи усилий обжатия на бетон, Rbp = 23 МПа.
α = 0,85 – коэффициент, учитывающий тепловую обработку бетона.
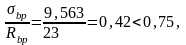
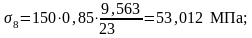
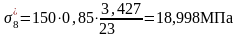
σ9 – потери от смятия спиральной арматуры:
σ9 = 0.
σ10 – потери от деформаций обжатия стыков между блоками:
Т.к. конструкция возводится на сплошных подмостях, то σ10 = 0.
Определим потери в стадии эксплуатации:

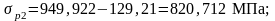
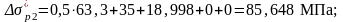
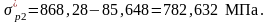
Этап 4 Расчет по трещиностойкости в стадии обжатия бетона
Данная проверка ограничивает значения напряжения в верхней и нижней фибрах балки с целью предотвращения появления трещин на стадии обжатия.
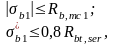
где Rb,mc1 – расчетное сопротивление бетона осевому сжатию на стойкость против образования продольных микротрещин, Rb,mc1 = 23 МПа;
Rbt,ser – расчетное сопротивление бетона осевому растяжению,
Rbt,ser = 2,2 МПа.
Искомые напряжения:
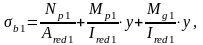
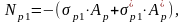
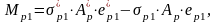
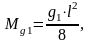
где
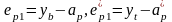 - эксцентриситеты приложения
равнодействующих сил натяжения
соответственно нижней и верхней арматуры.
- эксцентриситеты приложения
равнодействующих сил натяжения
соответственно нижней и верхней арматуры.

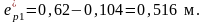
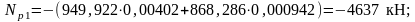
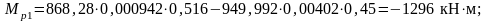
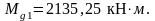
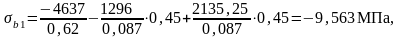
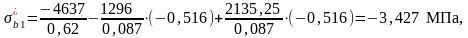
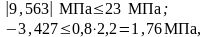
Проверки по образованию трещин проходят, назначенные напряжения в арматуре могут быть приняты на данном этапе расчёта.
Этап 5 Расчет в стадии эксплуатации по трещиностойкости без временной нагруки
Расчетная проверка на данной этапе записывается в виде:
 ,
,
где σb2 – напряжения в бетоне (крайних волокнах балки) на стадии эксплуатации с учетом потерь напряжений в арматуре. Вычисляется по формуле:
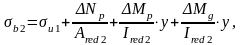
где ΔNp и ΔMp – уменьшение внешних нагрузок за счет снижения усилий в ПНА, вызванных потерями второй группы:

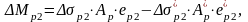
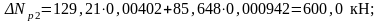
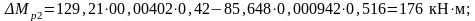
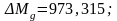
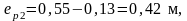
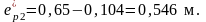
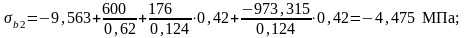
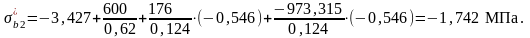
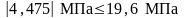
Условие выполняется.
Этап 6 Расчет в стадии эксплуатации по трещиностойкости от нормативных постоянных и временных нагрузок
Условия проверки:
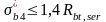 =1,4∙2,2=3,08
=1,4∙2,2=3,08
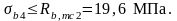
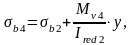
где Mv4 – момент, создаваемый подвижной нагрузкой, Mv=2435,750кН∙м.
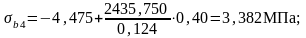
3,382МПа < 19,6 МПа. Условие выполняется.
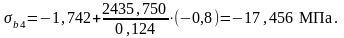
-17,456 МПа < 3,08 МПа. Условие выполняется.
Сжимающие напряжения в нижней части не превышают допускаемых.
Возникающие в верхней грани ригеля напряжения являются сжимающими, следовательно, нормальные трещины не образуются.
Этап 7 Расчет на выносливость от регулярно обращающейся нагрузки
Главные балки автодорожных мостов на выносливость не рассчитываются.
Этап 8 Построение огибающей эпюры материалов и нахождение мест расположения внутренних анкеров
Принимается допущение, что каждый пучок воспринимает одинаковую долю момента. Эпюра материалов – см. прил. 2.
Этап 9 Расчет приопорного сечения балки по ограничению касательных напряжений в стадии эксплуатации
Приверку рекомендуется делать на расстоянии 1,0 и 1,5м от опирания, но для упрощения принимать значение поперечной силы в опорном сечении.
Касательные напряжения на уровне центра тяжести сечения должны удовлетворять условию:
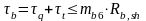
где
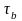 - касательные напряжения в бетоне;
- касательные напряжения в бетоне;
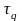 - касательные
напряжения от поперечной силы;
- касательные
напряжения от поперечной силы;
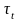 - касательные
напряжения от кручения (в курсовом
проекте не учитываем);
- касательные
напряжения от кручения (в курсовом
проекте не учитываем);
 - расчетное
сопротивление бетона скалыванию;
- расчетное
сопротивление бетона скалыванию;
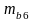 - коэффициент
условий работы.
- коэффициент
условий работы.
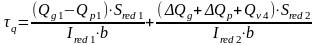
где
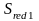 ,
,
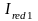 - геометрические характеристики
приопорного сечения без учета арматуры,
но с учетом каналов, подсчитаны в ЕХЕL;
- геометрические характеристики
приопорного сечения без учета арматуры,
но с учетом каналов, подсчитаны в ЕХЕL;
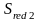 ,
,
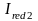 - геометрические характеристики
приопорного сечения с учетом арматуры,
подсчитаны в EXEL;
- геометрические характеристики
приопорного сечения с учетом арматуры,
подсчитаны в EXEL;
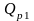 - поперечная сила
от первой части постоянных нагрузок;
- поперечная сила
от первой части постоянных нагрузок;
Q p1, DQg, Qv4 - нормативные значения поперечной силы от первой, второй частей постоянных нагрузок и от подвижной нагрузки;
 -
поперечная сила от усилий в отогнутой
арматуре с учетом всех потерь (в
рассматриваемом сечении нет отогнутых
пучков, поэтому Qр=0);
-
поперечная сила от усилий в отогнутой
арматуре с учетом всех потерь (в
рассматриваемом сечении нет отогнутых
пучков, поэтому Qр=0);
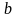 - толщина ребра
балки.
- толщина ребра
балки.
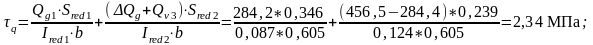
Rb,sh=3,6 МПа; mb6=1+σby/Rb,sh=1+1,035/3,6=1,29; где σby – нормальное сжимающее напряжение в бетоне при 3 уровне загружения в опорном сечении.
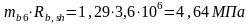
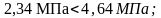 Условие
выполняется.
Условие
выполняется.
Этап 10 Расчет приопорного сечения балки на поперечную силу
Необходимо выполнить две проверки:
а) проверка прочности на сжатие между трещинами:
Условие прочности сжатого бетона между наклонными трещинами:
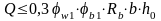 ,
,
где Q - поперечная сила на расстоянии не ближе h0 от оси опоры,
Q = 2892,3кН;
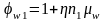 ,
,
где η=5 (хомуты нормальны к продольной оси балки /1, п.3.77/); n1= Es/Eb = 5,56 – отношение модулей упругости арматуры и бетона;
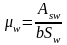 ,
,
где
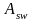 – площадь ветвей хомутов, расположенных
в одной плоскости,
– площадь ветвей хомутов, расположенных
в одной плоскости,
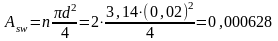 м2;
м2;
 -расстояние
между хомутами по нормали к ним (на
приопорном участке
=15см).
-расстояние
между хомутами по нормали к ним (на
приопорном участке
=15см).
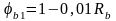
Таким образом
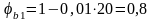
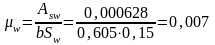
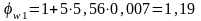
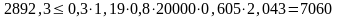 кН
кН
2892,3 кН < 7060 кН
б) проверка достаточности поперечного армирования
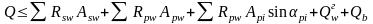
где
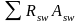 - сумма усилий в вертикальных хомутах,
пересекаемых наклонным сечением;
- сумма усилий в вертикальных хомутах,
пересекаемых наклонным сечением;
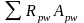 -
сумма усилий в хомутах предварительно
напряженной арматуры (хомуты ПНА
отсутствуют);
-
сумма усилий в хомутах предварительно
напряженной арматуры (хомуты ПНА
отсутствуют);
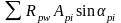 -
усилия отогнутой предварительно
напряженно арматуре (в данном случае
отогнутая арматура в сечение не попадает);
-
усилия отогнутой предварительно
напряженно арматуре (в данном случае
отогнутая арматура в сечение не попадает);
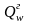 -
поперечная сила, воспринимаемая
горизонтальной арматурой;
-
поперечная сила, воспринимаемая
горизонтальной арматурой;
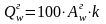 ,
,
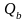 -
поперечное усилие, передаваемое на
бетон сжатой зоны над концом наклонного
сечения:
-
поперечное усилие, передаваемое на
бетон сжатой зоны над концом наклонного
сечения:

где
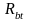 -
расчетное сопротивление бетона осевому
растяжению;
-
расчетное сопротивление бетона осевому
растяжению;
где с – горизонтальная проекция наклонного сечения с = 2,043м.
 -
коэффициент, зависящий от наибольшего
скалывающего напряжения
,
но в пределах 1,3 <
m
< 2,5.
-
коэффициент, зависящий от наибольшего
скалывающего напряжения
,
но в пределах 1,3 <
m
< 2,5.

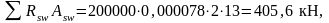
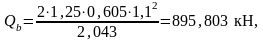
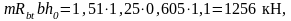
895,803 кН < 1256 кН.
895,803 кН < 895,803 + 405,6= 1301,4 кН.
Условие проверки выполняется.
Этап 11 Расчет наклонного сечения на раскрытие наклонных трещин
Ширина раскрытия нормальных и наклонных к продольной оси трещин аcr, в железобетонных элементах, проектируемых по категориям требований по трещиностойкости 2б, За, 3б и Зв:
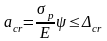
где в данном расчёте
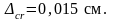
Приращение растягивающего напряжения р в напрягаемой арматуре, возникающее после снижения под временной нагрузкой предварительного сжимающего напряжения в бетоне до нуля, допускается определять по формуле:
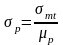 ,
,
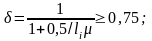 δ
– эмпирический коэффициент перераспределения
напряжений по наклонной трещине;
δ
– эмпирический коэффициент перераспределения
напряжений по наклонной трещине;
li – длина предполагаемой наклонной трещины по направлению, перпендикулярному главным растягивающим напряжениям на участке между вутами поясов – продольная арматура не попала в зону трещины.
σmt = +2,39МПа
p — коэффициент армирования, определяемый как отношение учитываемой в расчете площади поперечного сечения продольной арматуры к площади всей растянутой зоны бетона (арматура, не имеющая сцепления с бетоном, при вычислении p не учитывается).
Коэффициент раскрытия трещин:
= 0,35Rr - для гладкой стержневой арматуры, арматурных пучков из гладкой проволоки и для стальных закрытых канатов;
Радиус армирования Rr:

где
Аr
- площадь зоны взаимодействия нормального
сечения, принимаемая ограниченной
наружным контуром и радиусом взаимодействия
 ;
;
– коэффициент, учитывающий сцепление арматурных элементов с бетоном, = 0,5;
n – число арматурных элементов с одинаковым номинальным диаметром d. Для пучков и канатов d соответствует наружному контуру арматурного элемента, d = 0,035м;
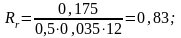
= 0,35*0,83 =0,29;
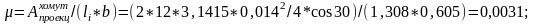
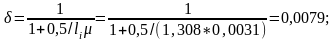
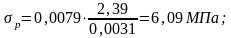
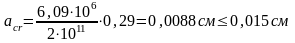 .
.
Величина раскрытия трещин не превышает допустимую – проверка проходит.
Этап 12 Расчет наклонного сечения в четверти пролета на образование трещин от главных напряжений
Наклонные трещины образуются от действия главных растягивающих и сжимающих напряжений, должны выполняться условия:
 ;
;
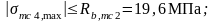
где главные растягивающие и сжимающие напряжения в бетоне:
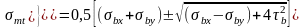 .
.
где bx - нормальное напряжение в бетоне вдоль продольной оси от внешней нагрузки и от усилий в напрягаемой арматуре с учетом потерь;
by – нормальное напряжение в бетоне в направлении, нормальном к продольной оси элемента, от напрягаемых хомутов, наклонной арматуры и напряжений от опорной реакции, при этом распределение сжимающих усилий от опорной реакции следует принять под углом 45;
b - касательное напряжение в бетоне стенки.
Нормальные напряжения по площадкам вдоль продольной оси элемента:
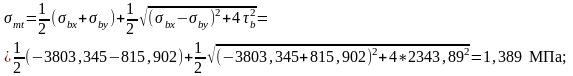
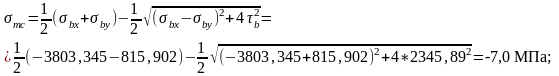
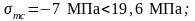
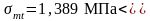 1,785МПа.
1,785МПа.
Проверка проходит.
Этап 13 Определение прогиба балки в середине пролета
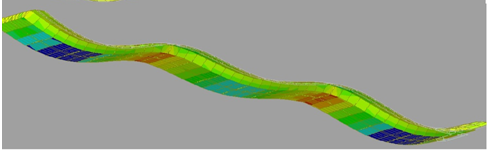
Рисунок 3.6 – Эпюра прогибов балки
Прогибы главной балки определим в программе Midas Civil.
Максимальный прогиб от временной нагрузки составляет 87мм от нормальной оси балки.
