Лабораторная работа №7

Модель Леонтьева

Имеется n отраслей. Рассматривается процесс производства за один год. Обозначим через х_i общий (валовой) объём продукции i-той отрасли, х_ij - объём продукции i-той отрасли, потребляемый j-той отраслью в процессе производства, у_i - объём конечного продукта i-той отрасли для непроизводственного потребления. Выполняются соотношения баланса:

х_i = Σ х_ij + у_i , i = 1,…,n, j = 1,…,n.

Коэффициенты прямых затрат

а_ij = х_ij / х_j

показывают затраты продукции i-той отрасли на производство единицы продукции j-той отрасли. Считаем, что а_ij = const. Тогда х_ij = а_ij · х_j , то есть

х_i = Σ а_ij · х_j + у_i .

Если обозначить вектор валового выпуска через

X= ,

матрицу прямых затрат через

А = ,

а вектор конечного продукта через

У= ,

то получаем матричное уравнение: Х = АХ + У.

Матрица А ≥ 0 (все элементы неотрицательны) называется продуктивной, если для любого вектора У ≥ 0 существует решение Х ≥ 0 этого уравнения. Модель Леонтьева в этом случае также называется продуктивной.

Условие продуктивности матрицы А: наибольшая из сумм элементов в столбцах матрицы А не превосходит 1, причем в А есть хотя бы один столбец, сумма элементов которого меньше 1.

Задание

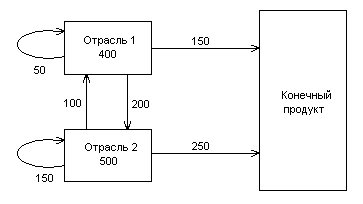
Выяснить продуктивность модели Леонтьева, учитывая схему:

Ход работы

По условию х₁ = 400, х₂ = 500, у₁ =150, у₂ = 250, х₁₁ = 50, х₁₂ = 200, х₂₁ = 100, х₂₂ = 150.

1. Находим элементы а_ij = х_ij / х_j матрицы А средствами Excel:

А = =

2. Вычисляем максимум сумм элементов в столбцах матрицы А:

max (0,125 + 0,25; 0,4 + 0,3) = 0,7 < 1 А - продуктивная матрица.

3. Пусть новый вектор валового выпуска

Х = ,

тогда из равенства Х=АХ+У получаем формулу для определения соответст­вующего вектора конечного продукта:

У = Х – АХ = (Е – А)Х =

Замечание: действия с матрицами выполняем средствами Excel. Для выполнения вычитания матриц, стоящих в скобках, необходимо разместить обе матрицы в некоторых диапазонах и определить диапазон для размещения результата вычислений. Затем в левую верхнюю ячейку новой матрицы ввести формулу для вычисления (например, для вычитания матриц) «=A1- A5» и скопировать ее методом протягивания в остальные ячейки диапазона, отведенного под результат. Для выполнения умножения матриц нужно выделить на рабочем листе блок ячеек под матрицу – произведение . Размер этой матрицы в данном случае будет 2×1. Затем следует воспользоваться функцией МУМНОЖ из категории Математические. В качестве аргументов этой функции указать диапазоны перемножаемых матриц и нажать сочетание клавиш CTRL+SHIFT+ENTER.

4. Зададим новый вектор конечного продукта

У =

и найдем соответствующий вектор валового выпуска

Х = (Е – А)^-1 У = .

Матрица (Е – А)^-1 называется матрицей полных затрат и определяется так: на рабочем листе нужно выделить блок ячеек под обратную матрицу и воспользоваться встроенной функцией МОБР из категории Математические. В качестве аргумента этой функции указать диапазон исходной матрицы и нажать сочетание клавиш CTRL+SHIFT+ENTER.