11Обработка результатов прямых измерений, содержащих случайные погрешности

14. Среднее арифметическое значение

Многократные (статистические) измерения проводятся с целью уменьшения влияния случайных погрешностей и повышения точности путем обработки результатов группы наблюдений. При повторении изме­рений мы получаем информацию только о случайной погрешности. О систематической погрешности из самих наблюдений извлечь информацию нельзя. Чтобы оценить эту погрешность, надо знать свойства исполь­зуемых средств измерений, метод измерения и условия измерения. В дальнейшем будем предполагать, что результаты измерений свободны от систематических и грубых погрешностей. Кроме того, будем счи­тать, что погрешности распределены по нормальному закону.

Измерения одной и той же величины, проводимые в одних и тех же условиях, одними и теми же людьми называются прямыми равноточ­ными измерениями.

В математической статистике доказано, что оценкой истинного математического ожидания измеряемой величины является среднее арифметическое результатов измерений.

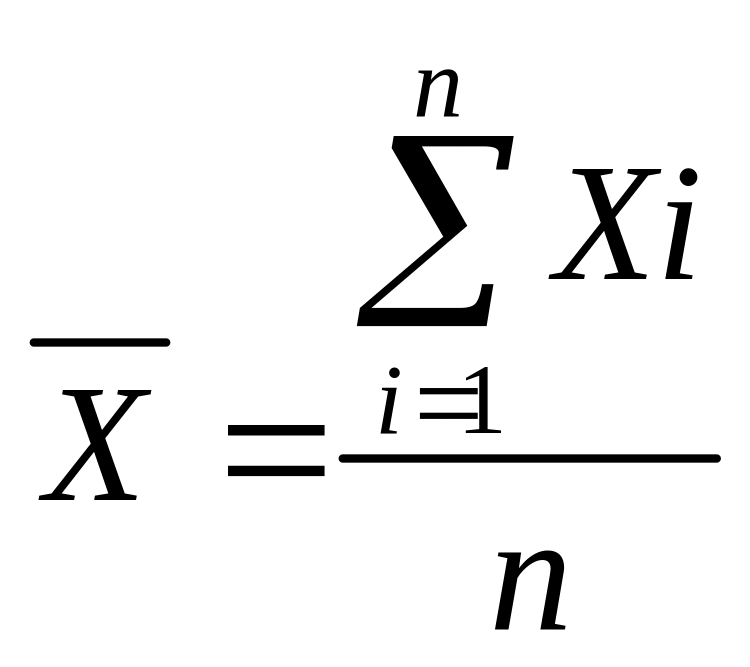
где Х_i - результат i- того измерения;

n - число измерений

Разность между результатом измерения и средним значением на­зывается случайным отклонением. Последнее имеет два важных свойс­тва.

1. Алгебраическая сумма случайных отклонений равна нулю, т.е.

Этим свойством можно воспользоваться для контроля правильнос­ти вычислений. Если при вычислении пользовались правилом округле­ний, то отклонение от нуля позволит оценить правильность округле­ний.

2. Сумма квадратов случайных отклонений имеет минимальное значение

Это следует понимать так. Если найти отклонение от любого другого числа, то сумма квадратов таких_{_} отклонений окажется боль­ше, чем сумма квадратов отклонений от .

15. Средняя квадратическая погрешность результата и сред­него арифметического

Несмещенная оценка среднего квадратического отклонение ре­зультата наблюдений определяется по формуле

Среднее значение вычисляют на основании конечного числа опытов n, следовательно, оно отличается от истинного на некоторую величину, другими словами, имеет погрешность. Если случайные пог­решности отдельных измерений подчиняются нормальному закону распределения, то и погрешность средних значений _i повторных рядов подчиняется этому же закону, но с другим меньшим рассеиванием.

Средняя квадратическая погрешность среднего арифметического , полученного из n измерений, определяется по формуле

При n → ∞ значение → 0, а значение стремится к истинному значению Х. Повышение точности результата измерения идет значительно медленнее, чем увеличение числа измерений. Так, чтобы увеличить точность в 10 раз, число измерений необходимо увеличить в 100 раз. Увеличение числа измерений имеет смысл только тогда, когда случайная погрешность является основной составляющей общей погрешности измерения. Если же преобладает систематическая погреш­ность и ее нельзя исключить, то увеличение числа n ничего не даст.

16. Вычисление среднего значения и средней квадратической погрешности с помощью произвольного числа

Когда числа многозначные и их много, пользоваться приведенны­ми выше формулами неудобно. Для облегчения расчетов выбирают про­извольно некоторое круглое или близкое к ожидаемому среднему число Х₀ . Тогда среднее значение и среднюю квадратическую погрешность можно определить по формуле

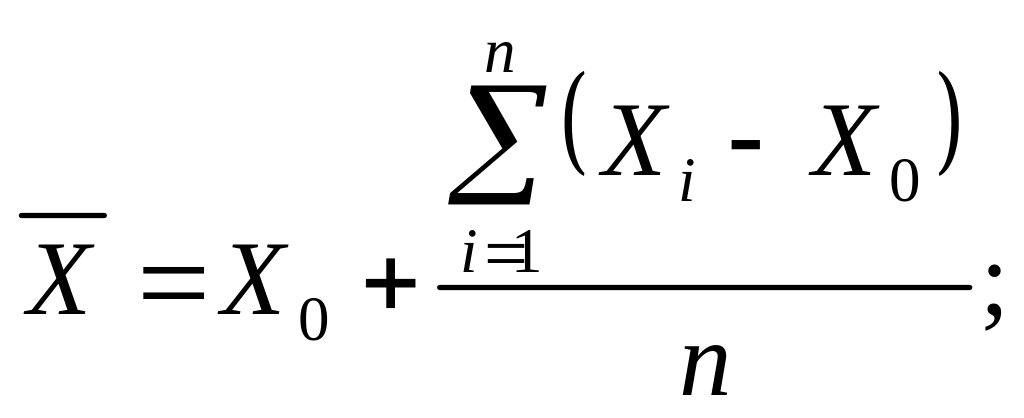
При расчете и δ обычно используют на одну значащую цифру больше, чем у исходных данных, а в окончательных результатах эту цифру отбрасывают, округляя число. Значение δ вычисляют с одной или двумя значащими цифрами. При этом следует помнить, что послед­ние цифры среднего значения и средней квадратической погрешности должны быть одного разряда.

17. Неравноточные измерения

До сих пор рассматривались измерения, заслуживающие одинако­вого доверия. Однако на практике приходится иметь дело с измерени­ями, выполненными с различной степенью точности или с различным числом измерений в каждой серии. В этом случае средние арифмети­ческие значения отдельных серий измерений одной и той же величины и средняя квадратическая погрешность этих серий могут отличаться друг от друга. Однако отбрасывать менее точные серии измерений не следует, так как увеличение числа измерений позволяет уменьшить случайную погрешность. Различная точность отдельных результатов оценивается так называемым "весом" - чем точнее результат серии, тем больший вес ему приписывается. Полученное таким путем среднее значение результата измерения называется средневзвешенным Х_с.

где - средние значения отдельных серий измерений;

- их вес.

Наиболее правильным значением веса для данного результата яв­ляется его вероятность. Если нет возможности определить вероят­ность, то числовые значения веса устанавливают исходя из условий измерений. Рассмотрим различные случаи.

1. Имеются средние значения, полученные на приборах разной точности. Вес измерений устанавливают обратно пропорциональным квадрату средней квадратической погрешности (дисперсии) Тогда

2. Имеются две серии с разным числом измерений, но с одинако­вой средней квадратической погрешностью δ.

Здесь вес измерений прямо пропорционален числу измерений в серии. Средняя квадратическая погрешность среднего взвешенного определя­ется по формуле

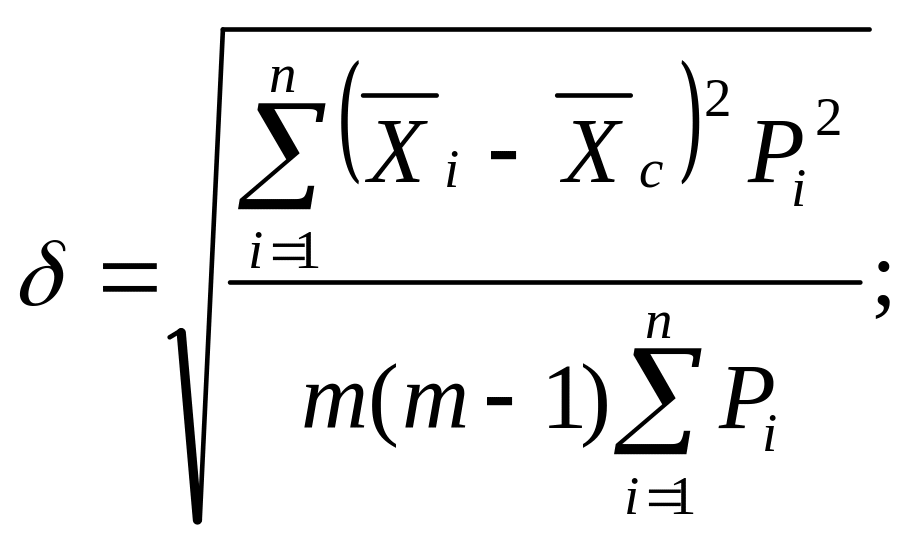
где m - общее число результатов измерений

18. Критерии грубых погрешностей

Ранее указывалось, что грубые погрешности (промахи) исключа­ются из общего ряда, поскольку они искажают результат измерений. Тем более это важно при малом числе измерений. Рассмотрим критерии оценки грубой погрешности.

Наиболее простым является отбрасывание результатов, имеющих погрешности, превышающие 3δ. Для этого предварительно обрабатывают полученный результат: находят среднее значение и среднюю квадрати­ческую погрешность. Определяют погрешность проверяемого результата Х_к - Х (Х_к - проверяемый результат измерения) и сравнивают с выб­ранным критерием 3δ. Результат, погрешность которого превышает выбранный критерий, содержит грубую погрешность и должен быть исключен из ряда. "Очищенный" ряд обрабатывают заново. Этот метод применим при достаточно большом числе измерений (n > 20).

При малом числе наблюдений более точные результаты дает кри­терий, основанный на распределении Стьюдента. Среднее значение и его среднюю квадратическую погрешность δ_х находят по результатам не всего ряда, а исключая проверяемый. Задаются некоторой вероятностью Р того, что проверяемая погрешность Х_к - Х не превысит зна­чения ε, которое определяется по формуле

ε = t _* δ_х ,

где t находят по таблицам вероятностей Стьюдента для заданных Р и n .

Пример: Произведено 5 измерений. Подсчитана δ_х = 0,5. Задав­шись доверительной вероятностью P = 0,9, по таблицам Стьюдента при n = 5 находим t = 2,13. Следовательно, если какая - либо из пог­решностей превысит величину ε = 2,13х0,5 = 1,065, то ее следует считать грубой и исключать из рассмотрения.