15Правила округлений

1. Округлять результат измерения следует так, чтобы он окан­чивался цифрой того же разряда, что и значение его погрешности. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасывают только до того разряда, который соответствует разряду числового значения погрешности.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то оставшиеся цифры числа не меняют. Лишние цифры в целых числах за­меняют нулями, а в десятичных дробях отбрасывают.

Примеры. Числовое значение результата измерения 39,5341 при погрешности в пределах ± 0,06 следует округлить до 39,53, то же число при погрешности ± 0,25 следует округлить до 39,534.

Число 325345 при сохранении четырех значащих цифр должно быть округлено до 325300, число 325,354 - до 325,3.

3. Если цифра старшего из отбрасываемых разрядов больше или равна пяти, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

Примеры. При сохранении трех значащих цифр число 13571 округ­ляют до 13600, число 131,57 - до 132.

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изме­няют, если она четная, и увеличивают на единицу, если она нечет­ная.

Примеры. Число 20,5 при сохранении двух значащих цифр округ­ляют до 20, число 21,5 до 22.

16Оценка погрешностей измерений с помощью вероятностной теории информации

23. Понятие энтропии информации и энтропийного значения погрешности

Измерение с точки зрения теории информации рассматривается как процесс, в результате которого уменьшается неопределенность в сведениях об измеряемой величине.

Меру неопределенности выражают энтропией, а информация выра­жается в тех же единицах, что и энтропия.

При измерениях вследствие погрешности измерительного прибора количество информации на выходе прибора всегда меньше количества информации на входе. Таким образом, в результате измерения получа­ем количество информации

q = Н (Х) - Н (∆) (16.1)

где Н (Х) - энтропия входного сигнала; Н (∆) - энтропия погрешнос­ти. Таким образом, увеличение информации об измеряемой величине уменьшает энтропию (исходную неопределенность), однако полного раскрытия неопределенности достигнуть невозможно из-за наличия пог­решностей измерения. Энтропия сигнала с плотностью вероятности Р (х), согласно К.Шеннону, определяется таким выражением

(16.2)

С позиций теории информации процесс измерения понимается как сокращение диапазона неопределенности измеряемой величины. Так, если прибор имеет пределы измерения от X₁ до X₂, то вероятность получения отсчета в пределах шкалы прибора равна единице, а за пределами шкалы - нулю .

Например, при равномерном распределении измеряемой величины в пределах от X₁ до X₂ начальная неопределенность об измеряемой ве­личине (до измерения) характеризуется малой плотностью вероятности (рис 16.1)

(16.3)

После измерения неопределенность сократилась до интервала неопре­деленности d = 2∆ и плотность вероятности увеличилась до величины

(16.4)

Иначе, энтропия значений измеряемой величины до измерения

Н (х) = ln ( Х₂ - Х₁) , (16.5)

а энтропия погрешности

Н (∆) = ln d = ln 2∆ , (16.6)

тогда количество информации

Последнее соотношение

q = ln N, если N = (Х₂ - Х₁) / d_э,

справедливо при любом законе распределения вероятностей погрешнос­ти, поэтому число N было предложено называть числом различных гра­даций измеряемой величины (числом эквивалентных делений) в диапа­зоне X₂ - X₁ при данном законе Р(х) распределения погрешности, а d_э - эквивалентным (в антропйном смысле) интервалом неопределенности.

Значение эквивалентного интервала неопределенности можно ма­тематически определить для любого закона распределения как величи­ну, стоящую под знаком логарифма в выражении для Н (∆), устраняя тем самым возможность какого - либо произвола.

Например, для нормально распределенной погрешности, т.е. при

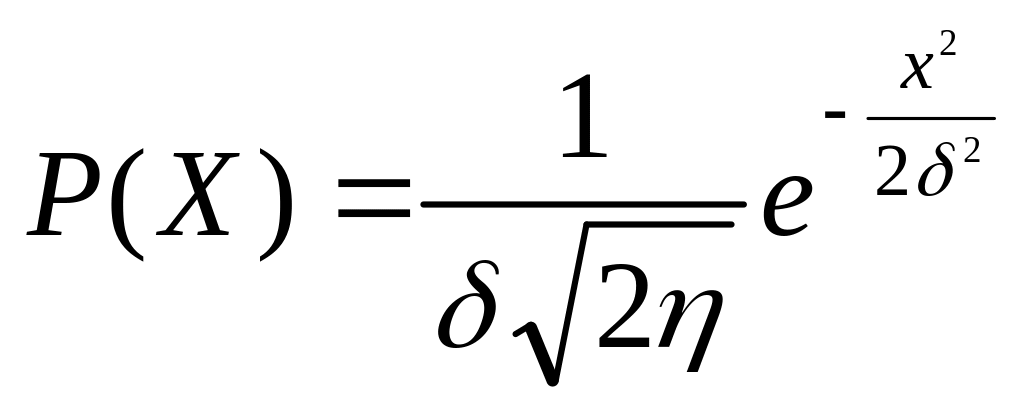(16.8)

и

(16.9)

получаем

(16.10)

Учитывая, что

= 1

и по определению дисперсии

=δ²

получаем

(16.11)

Тогда эквивалентный интервал неопределенности

(16.12)

Аналогично можно получить, что при равномерном законе распределе­ния погрешности

, (16.13)

а число различимых градаций измеряемой величины

(16.14)

Разделение диапазона X₂ - X₁ измеряемой величины на отдельные различимые градации на основании формальных приложений теории ин­формации в виде функционала (16.14) для энтропии представлено на рис (16.2). Здесь диапазон X₂ - X₁ разбит на эквивалентные интервалы d_э, вычисленные указанным выше путем, и относительно центра каждо­го такого интервала как начала координат построена кривая соответствующего закона распределения погрешности (равномерного, треу­гольного и нормального).

Из рисунка видно, что смысл шенноновского определения энтро­пии помехи состоит в том, что только при равномерном распределении погрешности границы интервалов неопределенности (логарифм числа которых есть количество информации q = lnN) совпадает с границами распределения погрешности, т.е. отдельные полосы погрешностей лишь соприкасаются между собой.

При треугольном, а тем более, при нормальном распределении погрешности эквивалентные интервалы уже размаха распределения пог­решностей и определяются лишь той частью распределения, где сосре­доточена основная масса этих погрешностей, а края распределений перекрываются.

При практическом использовании приведенных соотношений удобнее оперировать с половиной интервала d_э, именуемой энтропийным значением погрешности ∆_э.

Формально энтропийное значение погрешности определяется из соотношений

Н(∆) = lnd_э = ln2∆_э

(16.15)

d_э = 2∆_э = е^H(∆); ∆_э =1/2 е^H(∆)

Соотношение между ∆_э и δ зависят от вида закона распределения и оп­ределяется энтропийным коэффициентом К = ∆_э/δ

Так, для нормального закона

(16.16)

Следовательно, К = 2,07

Для треугольного закона (Симпсона) К = 2,02

Для равномерного закона

= 1.73δ; К = 1.73 (16.17)

Одним из достоинств энтропийного значения погрешности являет­ся очень простая связь мощности помехи δ² с вносимой ею дезинфор­мацией Н(∆) или с получаемым при измерении количеством информации q, а именно

(16.18)

исключая допускаемый без этого произвол. Действительно, до применения теории информации не было формального логического обоснован­ного соотношения между среднеквадратическим δ и практически норми­руемым ("предельным") ∆_m значениями погрешности. Так, при равно­мерном законе распределения указывают ∆_m = 1.73δ, а при нормальном законе ∆_m = 2δ при Р_q = 0.955 либо ∆_m = 3δ при Р_q = 0.997.

Как видно из изложенного выше, энтропийное значение погреш­ности почти точно соответствует практически используемым сейчас оценкам случайных погрешностей. Иначе говоря, используемая в нас­тоящее время оценка в виде ∆_m из серии 20-30 наблюдений очень

близка к именно энтропийному значению погрешности.

24. Единицы измерения энтропии и количества информации

Единица измерения энтропии и информации зависит от выбора ос­нования логарифма. При теоретическом анализе удобно использовать натуральные логарифмы и тогда энтропия и информация измеряются в так называемых натуральных единицах (сокращенно - нит).

При анализе устройств, работающих в двоичном коде (например ЭЦВМ), используют двоичные логарифмы и тогда информацию получают в двоичных единицах (сокращенно - бит). И наконец, при анализе уст­ройств, работающих в десятичном коде, получают десятичные единицы энтропии (сокращенно - дит).

Соотношение между этими единицами следующее:

1дит = 2,3 нит = 3,6 бит; 1 нит = 1,45 бит = 0,43 дит; 1 бит = 0,69 нит = 0,3дит.

Следует помнить, что в вычислениях значения X и ∆ должны подставляться в одних и тех же единицах.

25. Вычисление энтропийного значения погрешности по экспериментальным данным

В соответствии с определением

Здесь Р (х) определяется из гистограммы, где для каждого столбца Р_i(х_i) = n_i/nd. При количестве столбцов m и координатах центров этих столбцов х_i получаем

(16.19)

Представив последнее выражение в виде

(16.20)

получаем выражение для оценки энтропийного значения погрешности

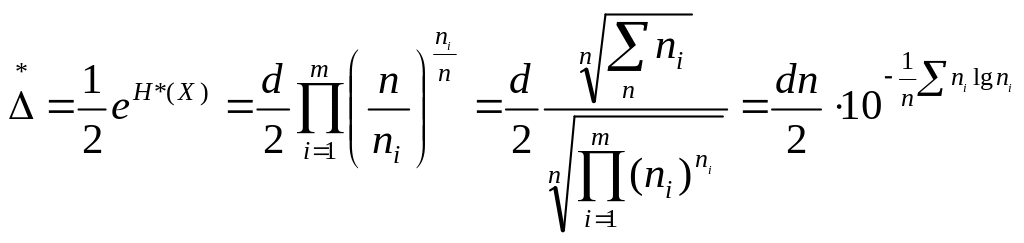(16.21)

Эта оценка является смещенной. Для введения поправки на смещение от недостаточно большого числа n_i наблюдений полученная оценка должна быть умножена на коэффициент

(16.22)

Л и т е р а т у р а

1. Орнатский П.П. Теоретические основы информационно - измери­тельной техники. - К.: Выща школа, 1976.- 432 с.

2. Рабинович С.Г. Погрешности измерений. Л.: Энергия, 1978.- 262 с.

3. Электрические измерения неэлектрических величин / под редакцией П.В.Новицкого.- 5-е издание. - Л.: Энергия, 1975.- 576 с.

4. Новицкий П.В. Основы информационной теории измерительных устройств.- Л.: Энергия, 1968.- 248 с.

5. Новицкий П.В., Зограф И.А. Оценка погрешности результа­тов измерений.- Л.: Энергоиздат, 1985.- 248 с.

6. Карасев А.И. Теория вероятностей и математическая ста­тистика.- М.: Статистика, 1970.- 344с.

61