13.3. Динамические сети

Следующий класс нейронных сетей, который мы рассмотрим, - дина­мические или рекуррентные, сети. Они построены из динамических нейро­нов, чье поведение описывается дифференциальными или разностными уравнениями, как правило, первого порядка. Сеть организована так, что ка­ждый нейрон получает входную информацию от других нейронов (возмож­но, и от себя самого) и из окружающей среды. Этот тип сетей имеет важное значение, так как с его помощью можно моделировать нелинейные динами­ческие системы. Это - весьма общая модель, которую потенциально можно использовать в самых разных приложениях, например: ассоциативная па­мять, нелинейная обработка сигналов, моделирование конечных автоматов, идентификация систем, задачи управления.

Нейронные сети с временной задержкой

П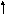еред тем, как описать собственно динамические сети, рассмотрим, как сеть с прямой связью используется для обработки временных рядов. Метод состоит в том, чтобы разбить временной ряд на несколько отрезков и полу­чить, таким образом, статистический образец для подачи на вход многослой­ной сети с прямой связью. Это осуществляется с помощью, так называемой разветвленной линии задержки (см. рис. 13.3).y(t)

X(t)

Рис.13.3. Нейронная сеть с временной задержкой

Архитектура такой нейронной сети с временной задержкой позволяет

моделировать любую конечную временную зависимость вида:

y(t) = F[ x(t), x(t - 1), ..., х(у - k)]. (13.17)

Поскольку рекуррентные связи отсутствуют, такая сеть может быть обручена при помощи стандартного алгоритма обратного распростране­ния ошибки или какого-то из его многочисленных вариантов. Сети такой конструкции успешно применялись в задачах распознавания речи, пред­сказания нелинейных временных рядов и нахождения закономерностей в хаосе.

СЕТИ ХОПФИЛДА

С помощью рекуррентных сетей Хопфилда можно обрабатывать неупо­рядоченные (рукописные буквы), упорядоченные во времени (временные ряды) или пространстве (графики, грамматики) образцы (рис. 13.4). Рекур­рентная нейронная сеть простейшего вида введена Хопфилдом; она построе­на из N нейронов, связанных каждый с каждым, причем все нейроны явля­ются выходными.

Сети такой конструкции используются, главным образом, в качестве ассо­циативной памяти, а также в задачах нелинейной фильтрации данных и грам­матического вывода. Кроме этого, недавно они были применены для предска­зывания и для распознавания закономерностей в поведении цен акций.

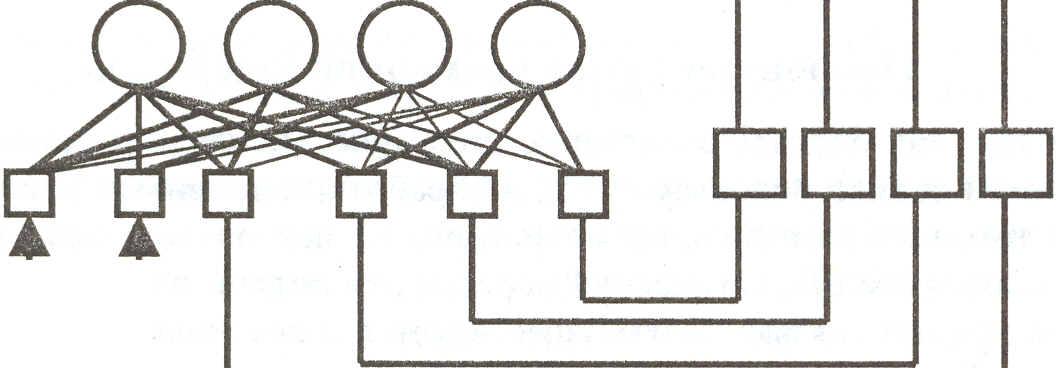
Входы

Рис.13.4.Сеть Холфилда

13.4. Самоорганизующиеся сети

Введенную Кохоненом «самоорганизующуюся карту признаков)} можно рассматривать как вариант нейронной сети. Сеть такого типа рассчитана на самостоятельное обучение: во время обучения сообщать ей правильные от­веты необязательно. В процессе обучения на вход сети подаются различныеобразцы. Сеть улавливает особенности их структуры и разделяет образцы на кластеры, а уже полученная сеть относит каждый вновь поступающий при­мер к одному из кластеров, руководствуясь некоторым критерием «близости".

Сеть состоит из одного входного и одного выходного слоя. Количество элементов в выходном слое непосредственно определяет, сколько кластеров сеть может распознавать. Каждый из выходных элементов получает на вход весь входной вектор. Как и во всякой нейронной сети, каждой связи припи­сан некоторый синоптический вес. В большинстве случаев каждый выход­ной элемент соединен также со своими соседями. Эти внутренние связи иг­рают важную роль в процессе обучения, так как корректировка весов проис­ходит только в окрестности того элемента, который наилучшим образом от­кликается на очередной вход.

Выходные элементы соревнуются между собой за право вступить в действие и «получить урок». Выигрывает тот из них, чей вектор весов окажется ближе всех к входному вектору в смысле расстояния, определяе­мого, например, евклидовой метрикой. У элемента-победителя это рас­стояние будет меньше, чем у всех остальных. На текущем шаге обучения менять веса разрешается только элементу-победителю (и, может быть, его непосредственным соседям); веса остальных элементов при этом как бы заморожены. Выигравший элемент заменяет свой весовой вектор, немного перемещая его в сторону входного вектора. После обучения на достаточ­ном количестве примеров совокупность весовых векторов с большей точ­ностью приходит в соответствие со структурой входных примеров - век­торы весов в буквальном смысле моделируют распределение входных об­разцов.

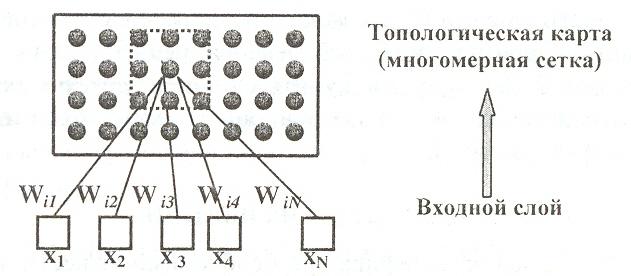
Puc.l3.5. Самоорганизующаяся сеть Кохонена. Изображены только связи, идущие в i-u узел. Окрестность узла показана пунктиром

Очевидно, для правильно го понимания сетью входного распределения нужно, чтобы каждый элемент сети становился победителем одинаковое число раз - весовые векторы должны быть равновероятными.

Перед началом работы сети Кохонена нужно сделать две вещи:

• векторы величины должны быть случайно распределены по единичной сфере;

• все весовые и входные векторы должны быть нормированы на едини­цу.

13.5. Сеть со встречным распространением

Сеть со встречным распространением (CPN, Counterpropagation Network) соединяет в себе свойства самоорганизующейся сети Кохонена и концепцию Oustar - сети Гроссберга. В рамках этой архитектуры элементы слоя сети Кохонена не имеет прямо го выхода во внешний мир, а служат вхо­дами для выходного слоя, в котором связям адаптивно придаются веса Гроссберга. Эта схема возникла из работ Хехта - Нильсена. CPN-сеть наце­лена на постепенное построение искомого отображения входов в выходы на основе примеров действия такого отображения. Сеть хорошо решает задачи, где требуется способность адаптивно строить математическое отражение по его точным значениям в отдельных точках.

Сети данного вида успешно применяются в таких финансовых и эконо­мических приложениях, как рассмотрение заявок на предоставление займов, предсказание трендов цен акций, товаров и курсов обмена валют. Говоря обобщенно, можно ожидать успешного применения СРN-сетей в задачах, где требуется извлекать знания из больших объемов данных.