
- •1. Организационно-методический раздел
- •1.1. Пояснительная записка
- •1.2. Требования к уровню освоения содержания дисциплины
- •2. Содержание дисциплины
- •2.1. Основные разделы дисциплины
- •2.2. Темы и их содержание
- •Тема 1. Элементы линейной алгебры.
- •Тема 2. Аналитическая геометрия на плоскости.
- •Тема 3. Аналитическая геометрия в пространстве.
- •Тема 4. Введение в анализ функций переменной.
- •Тема 5. Производная и дифференциал.
- •Тема 6. Интегральное исчисление
- •3. Рабочая программа дисциплины
- •3.1. Распределение часов курса по темам и видам работ
- •3.2. Формы текущего, промежуточного и итогового контроля.
- •4. Учебно-методическое обеспечение дисциплины
- •4.1. Перечень теоретических вопросов к экзамену
- •4.2. Примерный перечень практических задач к экзамену
- •4.3. Список литературы
- •4.4. Использование информационных технологий
- •Дополнения и изменения в рабочей программе на 20___ – 20___ учебный год
3.2. Формы текущего, промежуточного и итогового контроля.
Программа по дисциплине «Математика» должна быть усвоена студентами в течение 1, 2 семестров – очное обучение полностью и с оценкой на уровне не ниже «удовлетворительно». Итоговый контроль: 1, 2-й семестры (очное обучение) – экзамен.
4. Учебно-методическое обеспечение дисциплины
4.1. Перечень теоретических вопросов к экзамену
1-й семестр
Определители второго и третьего порядка.
Свойства определителей.
Формула Крамера. Метод Гаусса (метод исключения неизвестных).
Взаимное расположение линии и точки.
Взаимное расположение двух линий.
Расстояние между двумя точками.
Деление отрезка в данном отношении.
Деление отрезка пополам.
Общее уравнение прямой.
Условие параллельности прямых.
Пересечение прямых.
Условие перпендикулярности двух прямых.
Угол между двумя прямыми.
Уравнение прямой проходящей через две точки.
Расстояние от точки до прямой.
Кривые второго порядка: окружность, центр и радиус окружности.
Кривые второго порядка: эллипс, каноническое уравнение эллипса.
Кривые второго порядка: гипербола.
Кривые второго порядка: парабола.
Понятие о векторах и скалярах.
Вектор в геометрии.
Коллинеарные векторы.
Нуль-вектор.
Равенство векторов.
Противоположные векторы.
Сложение векторов. Вычитание векторов.
Умножение и деление вектора на число.
Длина вектора.
Расстояние между двумя точками.
Признак коллинеарности (параллельности) векторов.
Деление отрезка в данном отношении.
Скалярное произведение двух векторов.
2-й семестр
Предел функции.
Основные теоремы о пределах.
Первый замечательный предел.
Второй замечательный предел.
Свойства пределов.
Раскрытие неопределенности вида 0/0.
Раскрытие неопределенности вида ∞/∞.
Свойства неопределенного интеграла.
Таблица интегралов.
Свойства определенного интеграла.
Производные некоторых простейших функций.
Свойства производной.
Выражение производной через дифференциалы.
Функция от функции (сложная функция).
Производная сложной функции.
Производная произведения.
Производная частного (дроби).
Производная показательной функции.
Производная логарифмической функции.
Производная тригонометрических функций.
Производная обратных тригонометрических функций.
Производные высших порядков.
4.2. Примерный перечень практических задач к экзамену
1-й семестр
Задача №1.
Вычислить
определитель

Задача №2.
Имеют ли прямая x+y=3 и окружность x2+y2=49 общие точки?
Задача №3.
Найти расстояние между точками М(2,3; 4,0) и О(8,5; 7,0).
Задача №4.
Дан ромб ABCD: A(-1;1), B(3;4), C(7;-1). Найти координаты точки D.
Задача №5.
Найти расстояние между точками М(8,-3,8) и К(6,-1,9)
Задача №6.
Длины векторов а и с равны соответственно 2м и 1 м, а угол между ними 120°. Найти скалярное произведение ас.
2-й семестр
Задача №1.
Вычислить предел
![]()
Задача №2.
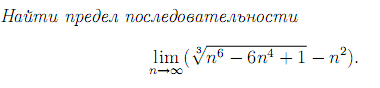
Задача №3.
Вычислить
предел
![]() .
.
Задача №4.
Вычислить
производную функции y=8x5+6![]()
Задача №5.
Вычислить
интеграл
![]()
Задача №6.
Вычислить
определенный интеграл
![]()
4.3. Список литературы
Атанасян Л.С. Геометрия. М., Просвещение, 1981.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 1971.
Берман Г.Н. Сборник задач по курсу математического анализа. М, Гостехиздат, 1973.
Вентцель Е.С. Исследование операций. Задачи, принципы, методология: Учеб. пособие для ВУЗов. - М.: Дрофа, 2004.
Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика, СПБ, Издательство «Лань», 2002.
Высшая математика для экономистов./ Под ред. Н.Ш. Кремера – М.: «Банки и биржи», Изд.объед. «ЮНИТИ», 1997.
Гончаров В.А. Методы оптимизации. М.: Высшее образование, 2009.
Грицюк С.Н. Математические методы и моделирование в экономике. Ростов-на-Дону, Феникс, 2007.
Дадаян А.А. Математика. М., ФОРУМ: ИНФРА-М, 2005.
Исследование операций в экономике./ Под ред. Кремера Н.Ш. – М.: «Банки и биржи», Изд.объед. «ЮНИТИ», 1997.
Кострикин А.И. Введение в алгебру. М., Наука, 1977.
Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономических специальностей. М.: Высшее образование, Юрайт-Издат, 2009.
Крюковский А.С., Растягаев Д.В. Математика. Ч1,Ч2. М., РосНОУ.
Куликов Л.Я. Алгебра и теория чисел. М., Высшая школа, 1979.
Новиков Ф.А. Дискретная математика для программистов. СПБ., ПИТЕР, 2004.
Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. М.: Высшая школа, 2008.
Партыка Т.Л., Попов И.И. Математические методы. М., ФОРУМ: ИНФРА-М, 2009.
Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов, М., Просвещение, 2004.
Привалов И.И. Введение в комплексный анализ. – М.: Наука,1984.
Солодовников А.С., Браилов А.В. Линейное программирование: Учеб пособ. по курсу «Математика в экономике». – М.: Финансовая академия при Правительстве РФ, 1996.
Фаддев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М., Наука, 1972.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. М., Наука, 1964.
Шипачев В.С. Высшая математика. М., Высшая школа, 2003.
Яблонский С.В. Введение в дискретную математику. М., Высшая школа, 2003.
