
Русилко_Лекция 1_lek
.pdf
1
Экономическая кибернетика
Лекция 1
ЭКОНОМЕТРИКА
Лекции для студентов 3 курса факультета математики и информатики специальности «Экономическая кибернетика»
Преподаватель: Русилко Татьяна Владимировна, кандидат физ.-мат. наук, доцент, доцент кафедры СА и ЭМ
Учебный план:
6-й семестр – 26 лекционный часов, 26 часов лабораторных занятий; 7-й семестр – 26 лекционный часов, 26 часов лабораторных занятий, контрольная работа, экзамен
ЛИТЕРАТУРА
1.Магнус, Я.Р. Эконометрика. Начальный курс / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий. – М.: Дело, 2004. – 576 с.
2.Мхитарян, В.С. Эконометрика / В.С. Магнус, М.Ю. Архипова, В.А. Балаш, О.С. Балаш, Т.А. Дуброва, В.П. Сиротин. – М.: Проспект, 2009. – 384 с.
3.Харин, Ю.С. Эконометричекое моделирование / Ю.С. Харин, В.И. Малюгин,
А.Ю. Харин. – Мн.: БГУ, 2003. – 313 с.
4.Яновский, Л.П. Введение в эконометрику / Л.П. Яновский, А.Г. Буховец. – М.:
КНОРУС, 2009. – 256 с.
5.Айвазян, С.А. Эконометрика. Краткий курс: учеб. пособие / С.А. Айвазян, С.С. Иванова. – М.: Маркет ДС, 2007. – 104 с.
6.Айвазян, С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики / С.А. Айвазян, В.С. Мхитарян. – М.: ЮНИТИ, 1998. – 1005 с.
7.Елисеева, И.И. Эконометрика / И.И. Елисеева. – М.: Финансы и статистика, 2005. – 576 с.
8.Елисеева. И.И. Практикум по эконометрике / И.И. Елисеева. – М.: Финансы и ста-
тистика, 2008. – 344 с.
9.Бородич, С.А. Эконометрика / С.А. Бородич. – Мн.: Новое знание, 2001. – 408 с.
10.Кремер. Н.Ш. Эконометрика / Н.Ш. Кремер – М.: ЮНИТИ-ДАНА, 2002. – 543 с.
11.Тихомиров, Н.П., Дорохина Е.Ю. Эконометрика / Н.П. Тихомиров, Е.Ю. Дорохи-
на. – М.: Экзамен, 2003. – 512 с.
12.Просветов Г.И. Эконометрика: задачи и решения / Г.И. Проветов. – М.: Альфа-
Пресс, 2008. – 192 с.
13.Бывшев В.А. Эконометрика / В.А. Бывшев. – М.: Финансы и статистика, 2008. – 480 с.
14.Кочетыгов А.А. Основы эконометрики / А.А. Кочетыгов, Л.А. Толоконников. –
М.: ИКЦ “МарТ”, 2007. – 344 с.
15.Доугерти, К. Введение в эконометрику / К. Доугерти. – М.: ИНФРА-М, 2001. – 402 с.
16.Кулинич, Е.И. Эконометрия / Е.И. Кулинич. – М.: Финансы и статистика, 2001. – 304 с.
2
Экономическая кибернетика
Введение в эконометрику
Эконометрика – одна из базовых дисциплин экономического образования во всем мире. К сожалению, до 90-х годов прошлого столетия эконометрика, по существу, не была признана в России и Беларуси, а поэтому не включалась в учебные планы подготовки специалистов экономического направления. Сегодня ситуация изменилась. Эконометрику изучают студенты экономических специальностей всех высших учебных заведений.
В1910 г. бухгалтером П. Цьемпой (Австро-Венгрия) был введен термин «эконометрия». Цьемпа пытался применить методы алгебры и геометрии к анализу данных бухгалтерского учета для получения нового представления о результатах хозяйствен-
ной деятельности. Исследователям хотелось достичь в экономике того, что И. Ньютон достиг в физике. В
настоящее время этот термин используется для того раздела эконометрики и теории экономического анализа, который изучает влияние факторов, формирующих результаты работы фирмы (предприятия).
Термин «эконометрика» был введѐн в 1926 году норвежским учѐным Р. Фришем для обозначения количественного подхода к исследованию экономических процессов.
Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика». Таким образом, сам термин подчеркивает специфику и содержание эконометрики как науки: количественное (математическое) выражение тех связей и соотношений, которые раскрыты и обоснованы экономической теорией.
Вконце 1930 г. в США было создано первое международное эконометрическое общество. С 1933 г. начал издаваться журнал «Econometrica». В 1941 г. появился первый учебник по эконометрике, автором которого был Я. Тинберген.
Однозначного определения эконометрики пока не существует.
Эконометрика – это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Эта наука позволяет найти количественное подтверждение или опровержение того или иного экономического закона либо гипотезы.
Эконометрика – это область на стыке экономической и математической науки, в рамках которой осуществляется разработка адекватных вероятностно-статистических моделей и их использования для принятия решений.
Эконометрика – быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим соотношениям.
Таким образом, цель эконометрики заключается в придании конкретного коли-
чественного выражения общим (качественным) закономерностям экономической теории на базе данных статистических наблюдений с использованием математикостатистического инструментария.
Эконометрика сформировалась в результате синтеза трѐх направлений.
1) Экономической теории.
Предмет исследования – экономические явления. Но в отличие от экономической теории эконометрика делает упор на количественные аспекты, а не на качественные. Например, экономическая теория утверждает, что спрос на товар с ростом цены убывает. При этом практически неисследованным остается вопрос, как быстро и по какому закону происходит это убывание. Эконометрика отвечает на этот вопрос для каждого конкретного случая.
2) Математических методов.
Изучение экономических процессов (взаимосвязей) в эконометрике осуществляется через математические модели. Но в отличие от математической экономии, которая

3
Экономическая кибернетика
строит эти модели без использования реальных числовых значений, эконометрика концентрируется на изучении моделей на базе эмпирических данных.
3) Статистической теории.
Экономическая статистика обеспечивает исследователя реальными экономикостатистическими данными, обработанными и представленными в наглядной форме. Эти данные обрабатываются с помощью методов математической статистики. Однако, в силу специфики статистических данных в экономике (например, в экономике невозможно проведение управляемых экспериментов), людям, занимающимся эконометрикой, приходится разрабатывать свои собственные методы, которые в математической статистике не встречаются.
В настоящее время эконометрика завоевала всеобщее признание. За вклад в развитие эконометрической науки присуждены Нобелевские премии по экономике:
1969 г. – Рагнару Фришу и Яну Тинбергену, стоявшим у истоков зарождения эконометрики как науки.
1980 г. – Лоуренсу Клейну за применение эконометрических моделей к анализу экономических колебаний и в экономической политике. Известен построением макроэконометрических моделей, основанных на системах одновременных уравнений.
1981 г. – Джеймсу Тобину. Тобин в 1958 г. придумал регрессию с цензурированной зависимой переменной, которую по его имени называют тобит (чтобы было похоже на логит/пробит). Но в пресс-релизе об этом почему-то забыли упомянуть.
1989 г. – Трюгве Хаавельмо за разработку и анализ одновременных (структурных) эконометрических уравнений.
1995 г. – Роберту Лукасу. Его исследования дали толчок развитию новой области эконометрики, в основе которой лежит теория рациональных ожиданий.
2000 г. – Джеймсу Хекману и Дэниелу Макфаддену за развитие моделей дискретного выбора.
2003 г. – Роберту Инглу и Клайву Грэнджеру за создание моделей условной гетероскедастичности и развитие теории коинтеграции временных рядов.
4
Экономическая кибернетика
ГЛАВА 1. МОДЕЛИ ПАРНОЙ РЕГРЕССИИ
1.1.Эконометрические модели и особенности их построения
1.1.1. Типы данных
При моделировании различных экономических процессов возможны два основных типа данных:
1.пространственные данные;
2.временные ряды.
Пространственные данные это совокупность значений x1, x2 , ..., xn анализиру-
емой экономической переменной, полученных для некоторой группы из n 1 объектов в фиксированный момент (период) времени.
Пример. Данные по курсам покупки наличной валюты на некоторый день, по обменным пунктам города Гродно.
Временным рядом (ВР) называется ряд значений x1 , x2 , ..., xT , анализируемой экономической переменной, соответствующих T (T 1) последовательным моментам
(периодам) времени. В отличие от пространственных данных временные ряды характеризуют динамику изменения анализируемой переменной во времени.
Пример. Ежедневные данные по курсу доллара США в обменном пункте N города Гродно. Курс валюты национального банка за 365 дней прошлого года.
Значения временного ряда регистрируются с фиксированным интервалом наблюдения. По интервалу наблюдения различают такие основные типы данных, как годовые, квартальные, ежемесячные, ежедневные и т.д.
Пример. Годовые значения макроэкономических показателей, например, ВВП, объема выпуска промышленной и сельскохозяйственной продукции. Квартальные данные процентных ставок. Ежедневные значения курсов ценных бумаг.
1.1.2. Общий вид эконометрических моделей
Опишем общий вид эконометрической модели. Пусть состояние исследуемого экономического процесса в момент времени t характеризуется переменной y , прини-
мающей значение yt . Эту переменную будем называть эндогенной (внутренней, объясняемой, выходной, результирующей) переменной. Состояние процесса, а следовательно, значения переменной yt , могут зависеть от различных факторов, среди кото-
рых можно выделить две группы:
1. Систематические, контролируемые (наблюдаемые) факторы, которые в моде-
ли представляются объясняющими переменными (входными, экзогенными, фактор-
ными, предикторными), или регрессорами. Значения этих переменных считаются известными к моменту времени t . В свою очередь они делятся на две группы:
- экзогенные переменные xt1, xt 2 , ..., xtm , характеризующие воздействие на исследуемый процесс со стороны внешних факторов;
- лаговые переменные yt 1, yt 2 , ..., yt l , соответствующие значениям эндогенной переменной в прошлые моменты времени, отстающие от момента t на шага (лага) назад.
2. Случайные, неконтролируемые факторы, приводящие к случайным отклонениям t ( t ) значений эндогенной переменной yt от ожидаемых согласно модели значений.

5
Экономическая кибернетика
Целью эконометрического моделирования рассматриваемого процесса явля-
ется построение по эмпирическим данным статистической модели вида:
yt f ( yt 1, yt 2 ,..., yt l , xt1, xt 2 ,...,xtm ; ) t , |
|
где yt f ( ; ) – функция, определѐнная с точностью до неизвестных параметров |
. |
Модель может также включать в правой части лагированные значения экзогенных переменных x .
Например, y – объем реализации продукции, x1 – затраты на рекламу, x2 – цена
продукции, x3 – объем выпуска продукции, тогда yt f ( yt 1, xt1, xt 2 , xt3; ) t ; y – урожайность капусты, x1 – количество внесенных удобрений, x2 – количество воды при
поливе, x3 – сорт капусты, тогда yt f (xt1, xt 2 , xt3; ) t .
При построении эконометрической модели приходится решать следующие за-
дачи:
1. выбор и экономическое обоснование вида зависимости f ( ; ) , а также пред-
определенных и экзогенных переменных;
2.статистическое оценивание параметров модели ;
3.статистическая проверка адекватности построенной модели.
1.1.3. Классификация эконометрических моделей
Эконометрические модели классифицируются по таким признакам как раз-
мерность модели, учѐт фактора времени и вид функциональной зависимости.
1.Размерность модели определяется числом M совместно анализируемых эндогенных переменных, т.е. числом уравнений, входящих в модель. По этому признаку модели делятся на:
- одномерные M 1 ;
- многомерные M 1 (системы одновременных уравнений).
2.Фактор времени. В зависимости от того, учитывается в модели фактор времени или нет, различают:
- статические модели, которые включают переменные, относящиеся к одному и тому же моменту времени. Как правило, такие модели возникают при анализе пространственных данных, также совместном анализе коинтегрируемых ВР.
- динамические модели – модели временных рядов, включающие лаговые значения анализируемых переменных.
3.Вид зависимости. По виду функциональной зависимости yt f ( ; ) модели
делятся на:
-линейные относительно ;
-нелинейные относительно ;
-внутренне линейные – нелинейные по параметрам, которые можно привести к линейным с помощью определенного функционального преобразования.
1.1.4. Основные этапы построения эконометрических моделей
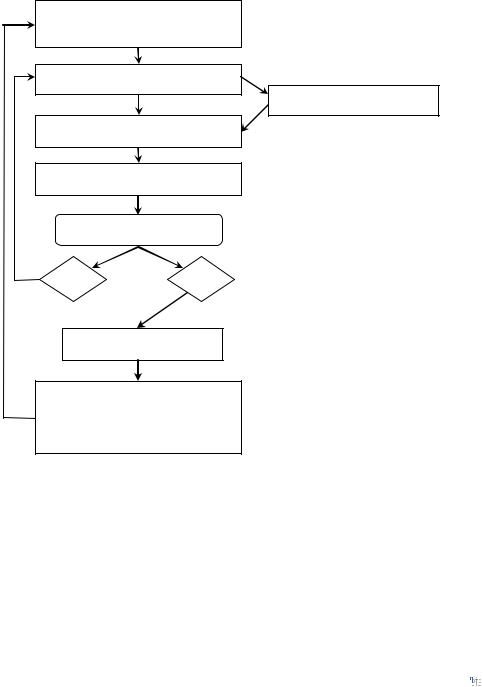
Схематически последовательность эконометрического анализа при разработке моделей можно представить с помощью блок-схемы на рисунке 1.1. На примере о стоимости квартир.
Этап 1. Экономическое обоснование модели:
-формулируются задачи и цели исследования;
-формируется состав экзогенных и эндогенных экономических переменных для включения в модель;
6
Экономическая кибернетика
-оцениваются возможности получения статистических данных определѐнного объема и интервала наблюдения (месяц, квартал, год и т.д.) для данного набора экономических переменных;
-проводится экономический анализ априорных взаимосвязей (существующих и предполагаемых) между анализируемыми переменными, формулируется ряд гипотез и исходных допущений об исследуемом явлении и разрабатывается общая структура модели.
Этап 2. Подготовка статистических данных:
-сбор и накопление необходимого объѐма статистических данных;
-представление значений экономических переменных в требуемом виде (например, в номинальных или реальных ценах, в виде темпов роста или темпов прироста, переход к логарифмам и т.д.);
-предварительный анализ с целью установления особенностей моделей (например, неоднородности для пространственных данных, нестационарности, наличия выбросов, скачков, сезонных эффектов и т.д.).
Экономическое обоснование теоретической модели
Эконометрическая модель
Статистические данные
Оценка параметров модели
Тестирование качества
Модель адекватна?
Нет |
Да |
Тестирование гипотез
Использование модели для прогноза и проведения экономической политики
Рисунок 1.1
Этап 3. Построение и анализ адекватности модели.
-спецификация моделей зависимости между эндогенными и экзогенными переменными, получение общего вида модельных соотношений, связывающих между собой исследуемые переменные;
-статистическое оценивание параметров моделей по имеющимся данным в рамках определѐнного класса моделей;
-тестирование адекватности построенных моделей на основе тестовых статистик и статистических критериев;
7
Экономическая кибернетика
- тестирование гипотез, предлагаемых экономической теорией, содержательная (экономическая) интерпретация свойств полученных моделей и оценка возможности их использования для решения задач исследования и прогнозирования. Например, величина и знак коэффициентов в модели должны согласовываться с теорией.
Этап 4. Использование модели.
-интерпретация полученных результатов, то есть перевод их с формализованного языка математики на содержательный язык рекомендаций по принятию управленческих решений;
-использование модели для прогноза и проведения экономической политики. Процесс построения эконометрической модели является итерационным, допус-
кающим возврат на более ранние этапы с целью учета новой информации и корректировки модели. Для решения задач третьего этапа часто требуется специальное про-
граммное обеспечение (Econometric Views, Statistica, STATA, SPSS, СЭМП и др.).
1.2. Суть регрессионного анализа
Регрессионный анализ является одним из наиболее распространенных инструментов эконометрического анализа. Термин «регрессия» ввел лорд Френсис Гальтон в конце 19-го века, исследуя связь между ростом родителей и детей. Он установил, что хотя у высоких родителей – высокие дети, а у невысоких чаще рождаются маленькие дети, рост детей имеет тенденцию к постепенному выравниванию, то есть стремится к средним значениям. Будучи аристократом, Ф. Гальтон к такой тенденции относился негативно и потому назвал ее регрессией (упадком).
Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с одной стороны, и статистическую или стохастически детерминированную – с другой. В естественных науках часто идѐт речь о функциональной зависимости, когда каждому значению одной переменной соответствует определенное значение другой переменной.
В эконометрике в большинстве случаев между переменными величинами существует зависимость, когда каждому значению одной переменной соответствует не ка- кое-то определенное, а множество возможных значений другой переменной. Иначе го-
воря, каждому значению одной переменной соответствует определенное (условное) распределение другой:
y / x xi |
yi1 |
yi 2 |
.... |
yin |
n |
n1 |
n2 |
.... |
nn |
|
|
|
|
|
Такая зависимость получила название статистической (стохастической или вероятностной). Примером статистической зависимости является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п. Возникновение статистической связи обуславливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также случайными ошибками измерений.
Если зависимость между двумя переменными такая, что любому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной. Иначе, корреляционной зависимостью между двумя переменными называется функ-
циональная зависимость между значениями одной из них и условным математическим ожиданием другой. Корреляционная зависимость может быть представлена в виде:
M ( y / x xi ) f (x), f (x) const . (1.1)

8
Экономическая кибернетика
Соотношение (1.1) называется моделью парной регрессии y на x . При этом зависимую переменную y называют эндогенной, а независимую x – экзогенной переменной или фактором. Уравнение (1.1) называют модельным уравнением регрессии, f (x) – модельная функция регрессии, а еѐ график – линия регрессии. Если в модели рассматривается m ( m 1) независимых переменных x1 , x2 , …, xm , то регрессия
M ( y / x1, x2 , ...,xm ) f (x1, x2 , ...,xm )
называется множественной.
Для отражения того факта, что реальные значения зависимой переменной не всегда совпадают с ее условным математическим ожиданием и могут быть различными при одном и том же значении x , фактическая зависимость должна быть дополнена некоторым слагаемым , которое по существу является случайной величиной и указывает на стохастическую зависимость:
y M ( y / x xi ) или y f (x) .
Простейшей регрессионной моделью является парная линейная регрессия: y 0 1x .
Существование в модели отклонений от уравнения регрессии, то есть присутствие случайного слагаемого , объясняется рядом причин.
1.Ошибки измерения. Например, при сборе данных об урожайности сельскохозяйственных культур, результаты могут завышаться или занижаться или оцениваться «на глазок» и т.д.
2.Невключение объясняющих переменных. Любая регрессионная модель являет-
ся упрощением реальной ситуации. Некоторые из факторов мы не можем включить в модель, так как не знаем, как их измерить, например психологические факторы. Возможно, существуют факторы, которые мы можем измерить, но которые оказывают такое слабое влияние, что их не стоит учитывать. Кроме того могут быть факторы, которые являются существенными, но из-за отсутствия опыта мы таковыми их не считаем. Например, спрос на товар определяется его ценой, ценой на товары заменители, доходом потребителей, их количеством, вкусами, ожиданиями и т.д.
3.Неправильный выбор вида зависимости в уравнении (функциональной специ-
фикации модели). Функциональное соотношение между переменными математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Любая самая изощренная формула является лишь приближением.
4.Агрегирование переменных. Во многих моделях рассматриваются зависимости между факторами, которые сами представляют сложную комбинацию других, более простых переменных. Например, зависимость между урожайностью и количеством внесенных удобрений индивидуальна для различных полей, и попытка определить зависимость между совокупной урожайностью и совокупным количеством внесенных удобрений является лишь приближением (аппроксимацией).
5.Ограниченность статистических данных. Зачастую строятся модели, выра-
жаемые непрерывными функциями. Но для этого используется набор данных, имеющих дискретную структуру.
6.Непредсказуемость человеческого фактора. Эта причина может испортить самую качественную модель.
Таким образом, случайный член является отражением влияния всех перечисленных причин и не только их. Большую опасность при практическом использовании методов регрессии представляют ошибки измерения и спецификации модели.
В парной регрессии выбор вида математической функции f (x) может быть осуществлѐн тремя методами:

9
Экономическая кибернетика
1.Графическим, с помощью графика, на котором точками отмечены все пары наблюдений (xi , yi ) , i 1, n . Такой график часто называют полем корреляции.
2.Аналитическим, который основан на изучении экономической природы (теории) взаимосвязи исследуемых признаков.
3.Экспериментальным.
