
- •Определители
- •Матрицы.
- •Системы линейных алгебраических уравнений
- •Кривые второго порядка
- •Элементы векторной алгебры
- •Скалярное произведение векторов
- •Векторное произведение
- •76. Вычислить определители:
- •Прямая в пространстве
- •Смешанные задачи на прямую и плоскость
- •Введение в математический анализ
- •Замечательные пределы
Замечательные пределы
152. Используя замечательные пределы найти предельные значения следующих выражений
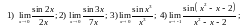
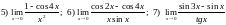 ;
;



Используя второй замечательный предел найти предельные значения следующих выражений

Вычислить указанный предел

Вычислить указанный предел 1)
 ;
;
Дифференцирование. Определения. Основные правила.
Вычислить приращение функции в точке

1)Используя определение производной функции и соответствующие
замечательные пределы вычислить производные данных функций
:
2)Написать уравнение касательной и нормальной прямой к функции
в точке :
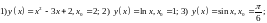
Найти точки пересечения полученных касательных с осями координат.
158.
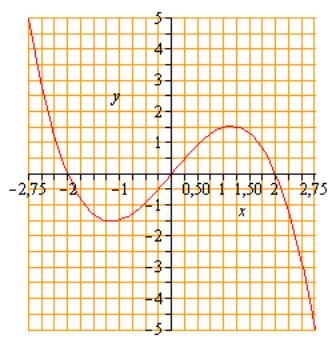
По данному
графику функции написать
приближённо уравнения касательных к
графику в точках заданных
координатами
написать
приближённо уравнения касательных к
графику в точках заданных
координатами
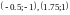 .
.
159.
Найти угол между
касательными проведенными в точках
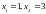
к графику
функции
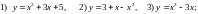
160. Найти угол между графиками функций и осью ОХ в указанных точках

161.
Найти острый угол
между графиками функций
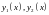 в
точке
в
точке
их пересечения

162. .
По оси
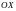 движется
точка, абсцисса которой с течением
движется
точка, абсцисса которой с течением
времени изменяется по закону
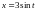 +2.
Определим абсциссу точки и её
+2.
Определим абсциссу точки и её
скорость и ускорение в моменты
времени: 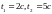 .
Определить
.
Определить
моменты времени, когда усилие действующее на точку равно: 1) нулю,
2) максимально.
163.
Пусть материальная точка движется
вдоль оси ОХ по закону
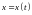 ,
где
,
где
- время:
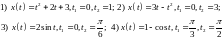
А. Вычислить среднюю скорость
за промежуток времени
 .
.
В.вычислить мгновенную скорость точки
в моменты времени
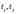
164. Найти координаты материальных точек, движущихся по закону
 ,
в момент времени когда
,
в момент времени когда
их скорости совпадают.
165. Вычислить производные функций
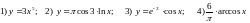


166. Вычислить производные функций

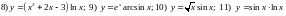

167. Вычислить производные функций

168.
Используя калькулятор, вычислить
производные функции в точке

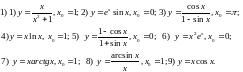
169. Найти функцию по заданной производной. Сделать проверку

170. Доказать,
что данная функция: 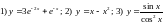
обращает соответствующее уравнение в тождество:
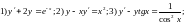
171. Найти вторые производные заданных функций
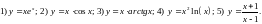
172. Доказать,
что функция
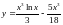 превращает
уравнение
превращает
уравнение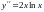
в тождество.
Функция от функции
173. Применив цепное правило вычислить производные функций

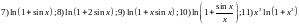 ;
;
 ;
;

23)
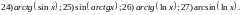
174. Используя калькулятор, вычислить производные функций в заданной точке
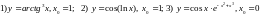
175.
Вычислить угол между
касательными к функции
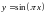 в точках.
в точках.
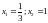 .
.
158.Используя равенства

доказать
формулы 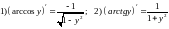
Логарифмическое дифференцирование
Вычислить производные заданных функций

Формулы неявного дифференцирования
177. Доказать, что данные формулы задают одну и туже кривую
линию
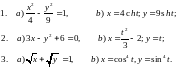
178. Применяя правило неявного дифференцирования, вычислить
производные от функций заданных неявно (уравнениями)

Найти первую и вторую производную функции заданной
неявно (уравнениями)
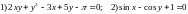 ;
;
Найти первую и вторую производную функции
 заданной
заданной
неявно (уравнениями)
;
Формулы параметрического дифференцирования
Вычислить и записать в параметрическом виде производные
 от
от
 функции
заданной
в параметрическом виде
функции
заданной
в параметрическом виде
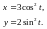
Вычислить и записать в параметрическом виде первую и вторую производные
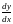 и
и
 от
функций
заданных
в параметрическом виде
от
функций
заданных
в параметрическом виде

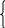

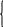
 4)
4)
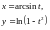
Написать уравнение касательной и нормали к кривым заданным
неявно
(уравнениями) в точке
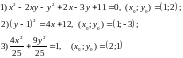
Написать уравнение касательной и нормали к кривым заданным
параметрическими уравнениями

Дифференциал функции
185. Используя таблицу найти дифференциалы следующих функций
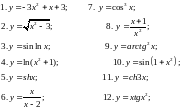
Изобразить геометрически приращение функции и дифференциал функции
при
заданных
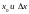 .
Оценить погрешность по графику
.
Оценить погрешность по графику
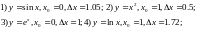
187. Получить
приближённые формулы справедливых для
малых

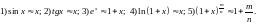
188. 1)
Используя формулу линейного приближения
функции , оценить максимальную
погрешность при
вычислении значения выражения
 ,
при
,
при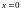 ,если
аргумент
задан
приближённо
,если
аргумент
задан
приближённо .
.
Используя формулу линейного приближения функции , оценить максимальную погрешность при вычислении значения выражения
 ,
,
при ,если
аргумент
задан
приближённо
,если
аргумент
задан
приближённо .
.
189.Вычислить значение данного выражения двумя способами: а) используя калькулятор и в) используя формулу линейного приближения функции .
1) (взять
(взять
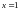 )
3)
)
3)
 (взять
(взять
 )
)
2)
 (взять
(взять );
4)
);
4)
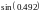 (взять
(взять
 ;
; ;
;
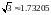 ).
).
190. Приближенно
измеренный радиус круга оказался
равным 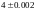 м.
м.
Используя формулу линейного приближения , оценить какова будет максимальная ошибка при вычислении
1) площади круга, 2) длины окружности.
191.
Приближенно измеренный радиус
шара оказался равным 1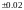 м.
м.
используя формулу линейного приближения , оценить какова будет
максимальная ошибка при вычислении
площади поверхности (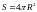 )
)
этого
шара. Для расчётов взять
 .
.
Приближенно измеренное ребро куба оказался равным
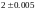 м.
Используя формулу линейного приближения,
оценить какова будет максимальная
ошибка при вычислении объёма куба и
площади поверхности куба.
м.
Используя формулу линейного приближения,
оценить какова будет максимальная
ошибка при вычислении объёма куба и
площади поверхности куба.
Правило Лопиталя
Записать формулу Лагранжа (о среднем в дифференцировании) для функций

194. Вычислить
указанные пределы

195. Вычислить указанные пределы
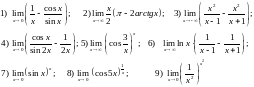
196 . Написать уравнения горизонтальных асимптот
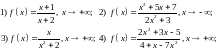
197. Написать уравнения горизонтальных и вертикальных асимптот и дать эскиз
графика функции

Приложение дифференцирования к задачам геометрии и механики
Найти острый угол между касательными прямыми к параболе
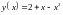 проведёнными в точках графика
проведёнными в точках графика
 .
.Найти точку пересечения касательных прямых проведенных к параболе
 в
точках
в
точках 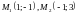 .
.Найти уравнение касательной прямой, проведённой к параболе
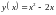 ,
,
параллельной
к прямой
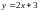 .
.
Найти уравнение касательной прямой, проведённой к параболе ,
перпендикулярной к прямой .
Найти расстояние от точки до касательной прямой, проведённой
к параболе
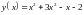 в
точке касания
в
точке касания
 .
.
Найти угол между графиками функций
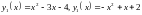
в точке их пересечения.
Под каким углом пересекают ось ОХ синусоиды:
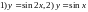
в точках:

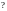
Под каким углом, и в какой точке касательная к кривой
 ,
проведённая в точке
,
проведённая в точке пересекает
ось ОХ
пересекает
ось ОХ
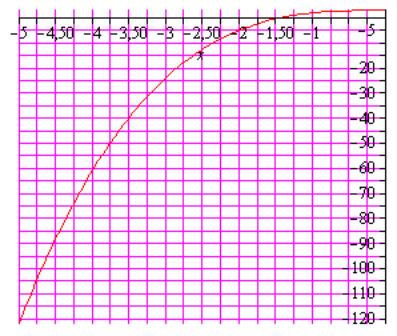
К какому классу монотонных функций принадлежит производная функции.Функция представлена на графике.
207.
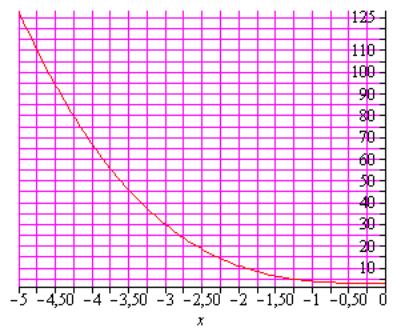
К какому классу монотонных функций принадлежит производная функции. Функция представлена на графике.
Дать эскиз графика любой функции заданной на интервале
 ,
для которой
,
для которой
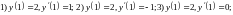
Изобразить на графике любую пару дифференцируемых функций ,
для
которых 
Cколько таких пар функций существует?
Секущая графика параболы
 проходит
через точку
проходит
через точку
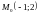 параллельно
касательной, проведённой к параболе в
точке
параллельно
касательной, проведённой к параболе в
точке
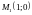 .
Найти
.
Найти
точку пересечения секущей и параболы.
Материальная точка движется по параболе
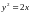 так,
что скорость изменения ординаты
так,
что скорость изменения ординаты
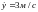 .
Найти мгновенную скорость изменения
абсциссы в точках
.
Найти мгновенную скорость изменения
абсциссы в точках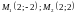 .
.Найти на гиперболе
 точку, в которой мгновенная скорость
точку, в которой мгновенная скорость
ординаты в два раза больше скорости абсциссы ;
ординаты равна скорости абсциссы ;
ординаты в два раза меньше скорости абсциссы ;
Материальная точка движется по эллипсу
 так,
что скорость изменения абсциссы
так,
что скорость изменения абсциссы ..
Найти мгновенную скорость изменения
ординаты в
..
Найти мгновенную скорость изменения
ординаты в .
.Материальная точка движется вдоль оси ОХ по закону
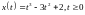 .
.
Найти моменты времени, в которые
скорость точки равна нулю;
сила действующая на точку равна нулю;
точка меняет направление движения;
определить
направление движения в моменты времени
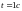 ,
,
 .
.
