
Перевод справки пакета SimPowerSystems программы Matlab / powersysSmall
.pdf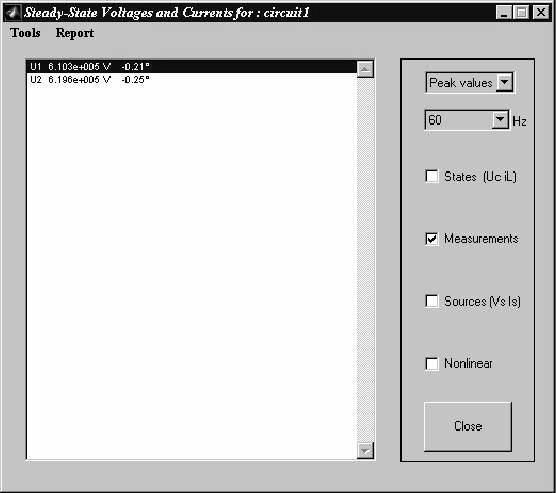
Раздел 2: Анализ простой схемы
Вэтом разделе вы будете:
9Использовать блок Powergui (графического интерфейса пользователя);
9Получать установившиеся характеристики системы;
9Анализировать вашу схему функцией power2sys;
9Анализировать электрическую схему в частотной области;
Анализ установившегося режима
Чтобы облегчать анализ установившегося режима вашей схемы, в библиотеке powerlib имеется GUI (графический интерфейс пользователя). Скопируйте блок Powergui в вашеокно circuit1 ищелкните два раза на блоке, чтобы его открыть. Перед вами откроется окно Steady State (установившегося режима), где показаны величины установившегося режима, измеренного двумя блоками измерения, отображенные в полярной форме.
31

Каждый вывод измерения сделан в отдельной строке, соответствующей имени блока измерения. Величина источников напряжения U1 и U2 соответствуетпиковому значению синусоидального напряжений.
Вокне Steady State (установившегося значения) вы можете также выбрать отображение установившихся значения исходного напряжения или установившихся значений устройств, поставив галочку напротив Sources (источников) или States (устройств).
К названиям устройств, например: катушек индуктивности или конденсаторов, для токов катушек индуктивности добавляется приставка II_, для напряжения конденсатора — Uc_.
Направления, напряжений и токов источников и устройств определены ориентацией блоков:
9Ток катушки индуктивности, протекающий отплюса к минусу считается положительно направленным;
9Напряжение конденсатора равно Ublock output -Ublock input ;
32

Примечание. Взависимости отномера блока в вашей диаграмме circuit1, некоторые переменные могутрасполагаться не в той последовательности, которая представлена на рисунке выше.
Теперь, в меню Tools блока powergui, выберите Initial Values of State Variables (начальные значения параметров устройств) / Display or Modify Initial State Values (просмотр или изменение начальные значений параметров устройств). Начальные значения этих шести параметров устройств (три тока для катушки индуктивности и три разности потенциалов для конденсатора) показаны перед вами. Эти начальные значения выданы по порядку, моделирование проводилось для установившегося режима.
33
Частотный анализ
Библиотека Measurement library of powerlib (измерения) содержит блок Impedance Measurement block (измерения полного сопротивления), который измеряетполное сопротивление между любыми двумя узлами схемы. Далее вы будете измерять полное сопротивление вашей схемы между шиной соединения B2 и заземлением, используя два метода:
1.Вычисление по состоянию модели;
2.Автоматическое измерение, использующее блок Impedance Measurement (измерения полного сопротивления) и блок powergui;
Вычисление характеристики полного сопротивления в функции частоты вмодели State-Space (режима-пространства)
Чтобы измерить полное сопротивление в функции частоты на соединительной шине B2, вам надо присоединить соединительной шину B2 с источником тока. Откройте библиотеку Electrical Sources (электрических источников), ископируйте блок AC Current Source (источник переменного тока) в вашу модель. Соедините этотисточник с соединительной шиной B2 как показано на рисунке 1-2. Установите амплитуду источника тока равной 0, а частоту 60 Гц. Перестройте блоки следующим образом.
Рисунок 1-2: AC Current Source (источник переменного тока) присоединенный к соединительной шине B2.
Теперь вычислим модель circuitl с помощью state-space (режим - пространства) представления функцией power2sys. Введите в командную строку
MATLAB’а.
[A, B, C, D, x0, states, inputs, outputs]=power2sys ('circuitl');
Функция power2sys возвращаетмодель state space (режим - пространства) вашейсхемы в четыре матрицы A, B, C, и D. X0 - вектор начальных условий, которые Вы только что выдели в блоке Powergui.
34
Имена переменных входов и выходов показаны в трех последовательных матрицах.
states =
Il_Z_eq
Uc_Z_eq
Il_110Mvar
Uc_input PI Section Line
Il_sect1 PI Section Line
Uc_output PI Section Line
inputs =
U_Vs
I_AC Current Source
outputs =
U_U1
U_U2
Обратите внимание, что вы смогли получить порядок имен переменных, входных и выходных непосредственно с помощью Powergui блока.
Как только модель state-space (режима-пространства) системы известна, можно проанализировать частотную зависимость. Например, один из способов для нахождения колебательных режимов этой цепи — с помощью вычисления собственных значений матрицы А(используйте eig команду в
MATLAB’е). eig(A)
ans = 1.0e+05 * -2.4972
-0.0001 + 0.0144i <---229 Hz -0.0001 - 0.0144i
-0.0002 + 0.0056i <---89 Hz -0.0002 - 0.0056i
-0.0000
35
Это устройство имеетдва колебательных режима: 89 Гц и 229 Гц. Колебания с частотой 89 Гц появляются из-за эквивалентного источника, который смоделирован единственным эквивалентом полюса. Колебания с частотой 229 Гц – первая гармоника линии, смоделированная для одной pi секцией.
Если вы имеете Control System Toolbox, вы можете вычислять полное сопротивление электрической цепи в функции частоты, используя тело функции.
Если использовать оператор Лапласа, то полное сопротивление Z2 шины B2 определяется как передаточная функция между током шины B2 (вход 2 системы) и напряжением, измеренным на шине B2 (выход 2 из системы).
= U (s) Z2 I22(s )
Полное сопротивление шине B2 в диапазоне 0-1500Hz можетбыть рассчитано и представлено следующим образом.
freq=0:1500;
w=2·pi·freq;
[mag1, phase1]=bode (A, B, C, D, 2, w); semilogy(freq,mag1(:,2));
Повторите тотже самый процесс, чтобы получить частотную характеристику для модели с 10 pi секциями. Откройте диалоговое окно PI Section Line, и замените число секций с 1 на 10.
Результаты представлены на рисунке 1-3.
36
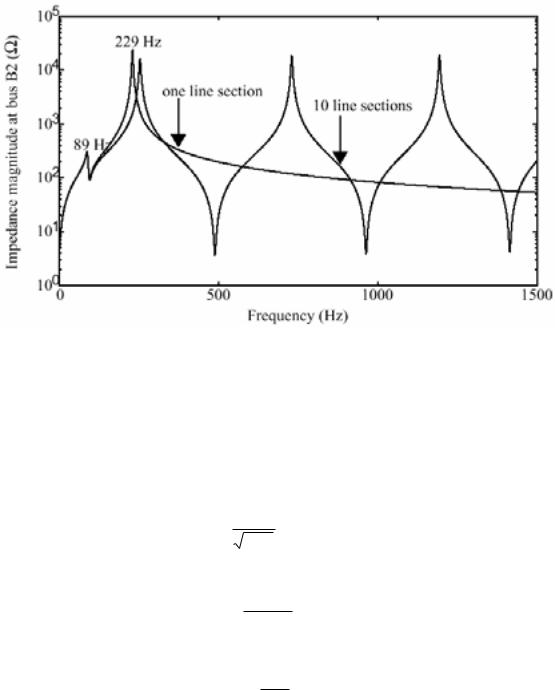
Рисунок 1-3: Полное сопротивление шины B2 в функции частоты
Этотрисунок показывает, что частотный диапазон, для модели с одной pi секции ограничен приблизительно 150 Гц. Для более высоких частот, модель с 10 секциями — лучшее приближение.
Для модели линии с распределенными параметрами скорость распространения равна
υ = |
1 |
= 293208 км \ с |
|
L C |
|
Время распространения будетдля 300 км — следовательно,
T = 293208300 = 1.023 мс,
а частота первой гармоники линии
f1 = 41T = 244 Гц.
Линия с распределенными параметрами имеетбесконечное число гармоник, каждые 244+n·488 Гц (n=1,2, 3...). Модель с 10 pi секциямилинии моделируетпервые 10 гармоник. Первые три гармоники представлены на ри-
сунке 1-3. (244Hz, 732Hz и 1220 Гц).
Вычисление полного сопротивления в функции частоты с помощью блока Impedance Measurement Block и блокаPowergui
Процесс, который мы описали выше, (измерение полного сопротивления), был автоматизирован в Power System Blockset. Откройте библиотеку
37

Measurements (измерений) библиотеки powerlib, и скопируйте блок Impedance Measurement block (измерения полного сопротивления) в вашу модель, переименуйте его на ZB2. Этотблок используетисточник тока и измеритель разности потенциалов, чтобы выполнить измерение полного сопротивления. Соедините два входа этого блока с соединительной шиной B2, и землёй, как показано на Рисунке 1-4.
Рисунок 1-4: Измерение полного сопротивления в функции частоты с помо-
щью блока Impedance Measurement block (измерения полного сопротивления)
Теперь откройте библиотеку powergui. Вменю Tools, выберите Impedance vs Frequency Measurement (измерение полного сопротивления в функции частоты). Откроется новое окно, в котором представлен список блоков Impedance Measurement blocks (измерений полных сопротивлений), доступных для вашей схеме.
38
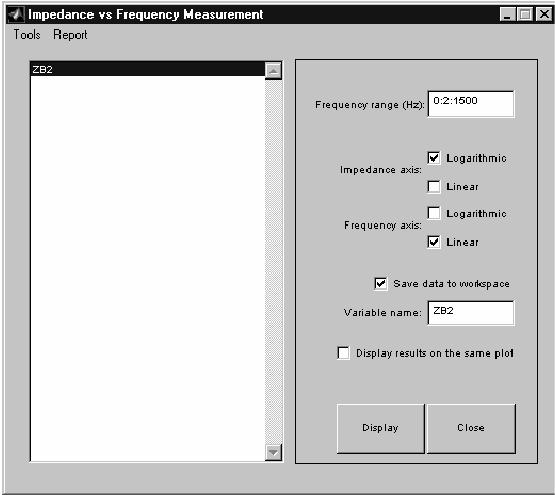
Ввашем случае, измерено только одно полное сопротивление, и оно представлено в окне идентификатором ZB2 (имя блока ZB2). Введите частотный диапазон, напечатав 0:2:1500 (от0 до 1500 Гцс шагом 2 Гц). Выберите логарифмическую шкалу для полного сопротивления. Щелкните кнопку Save data to workspace, и введите в текстовое поле ZB2 — имя переменной, которое будетсодержать полное сопротивление в функции частоты. Щелкните на кнопке Display.
Когда закончится расчет, появится графическое окно с амплитудой и фазой полного сопротивления в функции частоты. Амплитуда должна быть идентична графику (для линии с одной pi секцией), показанным на рисунке 1-3. Если вы посмотрите в ваше рабочее пространство, вы должны увидеть там переменную по имени ZB2. Это - матрица с двумяколонками, содержащая частоту в колонке 1 икомплексноесопротивление в колонке 2.
Теперь откройте меню Simulation/Parameters вашей модели circuit1. В секции Solver (решающего устройства), выберите алгоритм интегрирования
— ode23tb. Установите relative tolerance (относительную погрешность) 1e-4 и оставьте auto (авто) для других параметров. Установите время остановки счета равное 0.05 с. Откройте scopes (измерители) и запустите моделирование.
39

Посмотрите на формы входных и выходных напряжений на ScopeU1 и ScopeU2. Так как главные переменные автоматически инициализированы, система имеетустойчивое состояние и синусоидальное напряжение.
Наконец откройте Powergui. Вменю Tools выбираютInitial Values State Variables / Display or Modify Initial State Value, нажать кнопку Reset to zero (т.е. установить все переменные в 0), а затем кнопку Apply. Повторно запустите моделирование, и наблюдайте переходный процесс, когдапитание линии равно нулю.
Рисунок 1-5: Получение падения напряжения на концевых участках U2 pi линии с 10 секциями
40
