
Перевод справки пакета SimPowerSystems программы Matlab / powersysSmall
.pdf
Катушка индуктивности 10 мГн (Ls) соединена последовательно с двигателем постоянного тока, чтобы сгладить ток якоря. Постоянное возбуждение осуществлено с помощьюсоединения блока DC Voltage Source (источник напряжения постоянного тока) с обмоткой возбуждения.
Сигналы, требуемые для включения GTO тиристора, генерируются гистерезисным регулятором тока, который вынуждает ток двигателя следовать за заданием в пределах ±h/2, (h - гистерезисный диапазон).
Регулятор тока - маскированный блок, который содержит
Контур регулирования скорости используетпропорциональноинтегральный регулятор, который построен с помощью блоков Simulink.
Симуляция электропривода постоянноготока
Запустите моделирование, выбрав Start (старт) в меню Simulation (моделирование) в Simulink. Установите параметры моделирования в меню Simulation Parameters (параметры моделирования) следующим образом.
Simulation time (время моделирования): Start Time (начальное время): 0, Stop time (конечное время): 1.2
Solver Type (тип решателя): Variable-step ode23tb (stiff/TR-BDF2)
Max Step Size (размер максимального шага): auto (авто) Initial Step Size (начальный размер шага): auto (авто) Relative Tolerance (относительная погрешность): 1e-3 Absolute Tolerance (абсолютная погрешность): 1e-3
Кривые напряжения, тока и скорости двигателя отображены на трех графиках scope (измерителя), соединены с переменными Vd, Ia и ω.
121
Как только моделирование закончится, Вы можете возвратиться в окно команд MATLAB, чтобы подробно исследовать результаты, используя функцию plot (график).
Пуск привода
Сейчас, мысмоделируем переходный процесс пуска электропривода постоянного тока. Инерции механической нагрузки не хватаетдля подробного исследования коммутации преобразователя. Задание скорости — ступенька от0 до 120 рад/с при t=0 с, и на выходе мы имеем ток и скорость двигателя постоянного тока.
Переходные характеристики пуска привода постоянного тока представлены на рисунке 2-14.
Обратите внимание на то, что вектор конечного состояния системы xFinal можетбыть сохранен, если вы поставите галочку в Workspace I/O/Save to workspace/Final state (рабочее пространство I/O/сохранить/конечное состояние) в окне Simulation Parameters (параметры моделирования). Он можетиспользоваться как начальное состояние в последующем моделировании, чтобы моделирование началось для установившегося режима.
122

Рисунок 2-14: Пуск привода двигателя постоянного тока
Кривые напряженияи токадля установившегося режима
Когда установившийся режим достигнут, Вы можете остановить моделирование и построить кривые тока Ia и напряжения Va, переданные в рабочее пространство MATLAB с помощью блока scope (измеритель).
Кривые тока и напряжения двигателя постоянного тока, полученные в конце режима пуска, показаны на рисунке 2-15.
123
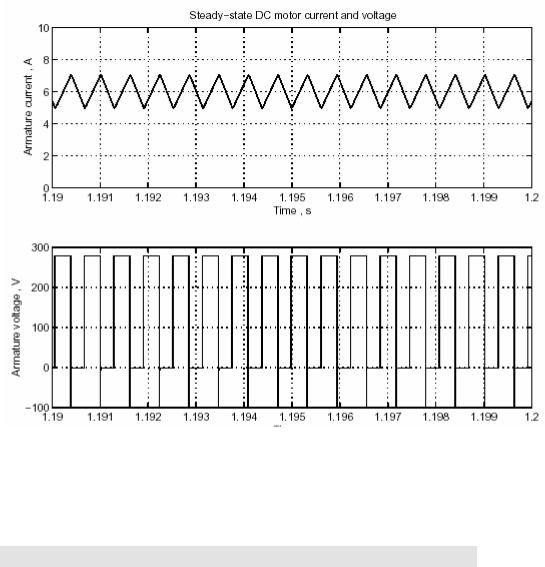
Рисунок 2-15: Кривые напряжения и тока двигателя для установившегося режима
Регулирование скорости Динамическая характеристика
Мы можем изучать динамическую характеристику привода, (изменяя задание скорости и вращающий моментнагрузки), с помощью изменения начальных условий электропривода постоянного тока: скачкообразно изменяя задание скорости и вращающий моментнагрузки.
Замените блок, названный wref (rad/s) и блок Load_torque (N.m) на два блока Simulink — step (скачек), с различными временами пуска. Скачек задания скорости от120 рад/с к 160 рад/с при t = 0.4 с искачек нагрузки вращающего момента от5 Н·м к 25 Н·м при t = 1.2 с. Вектор конечного состояния, полученный в предыдущем моделировании можетиспользоваться как начальное состояние, чтобы моделирование началось с установившегося режима. Загрузите файл psbdcdrive_init.mat , который создастпеременную xInitial. Выберите Workspace I/O/Load from workspace/Initial state (рабочее пространство I/O/загрузить из рабочего пространства/начальное состояние) в окне Simulation Parameters (параметры моделирования), и повторно запустите моделирование.
124
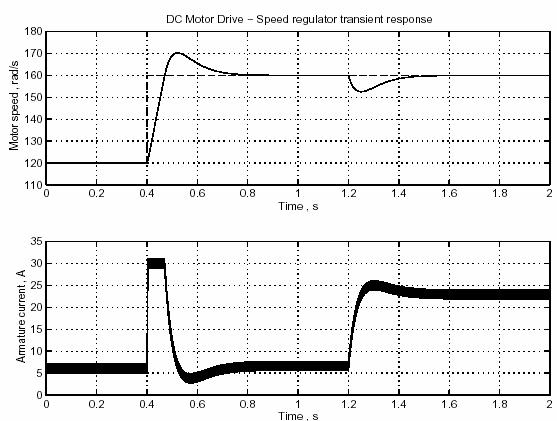
Полученные кривые привода двигателя постоянного тока для изменения скорости и нагрузки вращающего момента, показаны на рисунке 2-16.
Рисунок 2-16: Динамический переходный процесс привода двигателя постоянного тока
Литература
[1] Leonhard, W. Control of Electrical Drives. Springer-Verlag, Berlin 1996.
125

Раздел 3: Синхронная машина и регуляторы
Этотпоказательный пример исследуетподключение мультивходного мультивыходного нелинейного регулятора к устройству, состоящему из гидравлической гидротурбины и синхронного генератора, связанного с шиной бесконечной мощности. Вся система смоделирована, с помощью блоков биб-
лиотеки Power System Blockset иSimulink.
Цель этого показательного примера состоитв том, чтобы продемонстрировать использование блока Synchronous Machine (синхронной машины) соединенного со сложной системой управления, построенной с помощью блоков Simulink. Регулятор базируется на обратной связи линеаризованной схемы. Его основная функция состоитв том, чтобы управлять углом выбега ротора, напряжением на зажимах, улучшать свойства устойчивости, и получить хорошую динамическую характеристику. Результаты моделирования покажут, что нелинейный регулятор можетзаменить стандартные линейные регуляторы и при этом давать лучшие результаты.
Введение
Традиционно, стабильность энергосистем обеспечивалась линейными регуляторами типа автоматического регулятора напряжения (АРН), регулятора скорости, или стабилизатора энергетической системы (СЭС). Эти регуляторы работаютс линеаризованными моделями энергетических систем вокруг рабочей точки.
Возрастающие требования на улучшение работы создали потребность в работе энергосистем за пределам рабочей точки и поэтому вне линейного участка. Нелинейности начинаютиметь существенный эффектособенно после неполадок, которые приводятк большим смещениям рабочей точки.
Этотпоказательный пример позволитВам ознакомится с проектом нелинейного регулятора, который принимаетво внимание все нелинейности модели. Цели регулятора состоятв том, чтобы регулировать, и напряжение на зажимах и внутренний угол выбега ротора. Входы регулятора — напряжение возбуждения поля и вентиль открытия гидротурбины.
Математическая модель
Рассматриваемая модель — single machine infinite bus (SMIB) (одна машина и шина бесконечной мощности) система, представлена на рисунке 2- 17. Машина — синхронный генератор, управляемая гидравлической гидротурбиной.
126

Рисунок 2-17: Диаграмма показательного примера
Динамические уравнения машины, которые используются, чтобы получить линейный регулятор обратной связи для блока трехфазной Синхронной машины, и гидравлической гидротурбины и блок регулятора (см. Главу 4, "Блоки"). Так как синхронная машина связана с шиной бесконечной мощности, dq напряжения на зажимах Vd и Vq ограничены уравнениями нагрузки. Для Park-transformed координат(ротор приведен к статору), мы можем написать
Vd |
id |
id |
|
id |
|
+V ∞ |
|
cos(δ −α) |
|
= Re |
+ Le |
−ωLe |
|
|
|
|
|
Vq |
iq |
iq |
|
−iq |
|
|
−sin(δ −α) |
|
Это уравнение можетбыть объединено с полной моделью SMIB системы в нелинейной форме state-space (состояние-пространство)
x& = F(x)+G(x)u
F(x) и G(x) заданы
127

Явные выражения коэффициентов А и g могутбыть найдены в Главе 4, «Блоки» и опущены здесь для простоты. Другие переменные уравнения statespace (состояние-пространство) x — вектор параметров состояния, и u — вектор входов. Они определены следующим образом.
x = [id |
iq ifd ikd ikq δ ω q G]T |
u =[Vfd |
uG ]T |
Токи id, iq и напряжения Vd, Vq — фактические линейные токи и напряжения на зажимах, на осях сдвинутых на 90° по фазе (d-q координаты). ifd и Vfd — ток и напряжение возбуждения. ikq и ikd — токи демпфирующих обмоток, и ωугловая скорость машины. d — электрический угол, отсчитываемый отсинхронно вращающегося статора. G и q — соответственно вентиль открытия и скорость потока гидротурбины. Наконец, uG - разность потенциалов, прикладываемая к серводвигателю вентиля.
128

Обратнаясвязь линеаризованной системы
Обратная связь линеаризованного устройства состоитв отбрасывании всех нелинейностей, чтобы получить линейное соотношение между входами и выходами в замкнутом контуре. Нелинейный закон управления, выведенный с помощью последовательной дифференциации каждого из выходов, пока, по крайней мере, один из входов не появляется. Рассмотрим первый выход - напряжение на зажимах Vt.
y1 =Vt = Vd2 +Vq2
Напряжение на зажимах — сложная функция параметров состояния, в которых вход управления Vfd появляется явно с умножающим коэффициентом очень маленького порядка. Мы поэтому игнорируем эту прямую зависимость между Vt и Vfd ивычисляем производную по времени для выхода y1.
Второй выход y2 — угол d, который должен быть дифференцирован три раза прежде, чем появятся входы.
129

Объединяя уравнения для выходов, получится следующая нелинейная система ввода - вывода.
y(1) α1 |
(x ) β11 (x ) |
0 u1 |
|
||||
1(3) |
= |
|
+ |
β21 |
(x) |
|
|
y2 |
α2 |
(x) |
|
β22 (x) u2 |
|
||
Отсюда легко выводится нелинейный закон управления.
u1 |
β11 (x ) |
0 |
−1 |
α1 |
(x) V1 |
|
||||
|
= |
β21 |
(x) |
|
|
− |
|
+ |
||
u2 |
|
|
β22 (x ) |
|
α2 |
(x) |
V2 |
|
||
Отсюда следуетв замкнутом контуре, для линеаризованных систем ввода - вывода
y(1) |
V1 |
|
1(3) |
= |
|
y2 |
V2 |
|
Как только устройство было линеаризовано, любой линейный закон управления можно применять, чтобы регулировать выходные координаты. Здесь, метод размещения полюсов был выбран, и следующий линейный закон управления был предложен.
V1 =k11 (Vt −Vtref )
V2 =k21 (δ −δref )+k22 (δ&−δ&ref )+k23 (δ&&−δ&&ref )+k24 (x9 − x9 ref )
Последнее слагаемое в уравнении для V2 представлено, чтобы стабилизировать внутреннюю динамику. Эта динамика возникает, потому что первоначальная нелинейная система имеетдевятый порядок, в то время как линеаризованное устройство имеетчетвертый порядок. Это называется partial lin-
130
