Тема 4. Похідна та її застосування

4.1. Обчислити границі:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ; 12) ;

13) ; 14) ; 15) ;

16) ; 17) ; 18) ;

19) ; 20) ; 21) ;

22) ; 23) ; 24) ;

25) ; 26) ; 27) ;

28) ; 29) ; 30) ;

31) ; 32) ; 33) ;

34) ; 35) ; 36) ;

37) ; 38) ; 39) ;

40) ; 41) ; 42) ;

43) ; 44) ; 45) ;

46) ; 47) ; 48) ;

49) ; 50) ; 51) ;

52) ; 53) ; 54) ;

55) ; 56) ; 57) ;

58) ; 59) ; 60) ;

61) ; 62) .

4.2. Відомо, що . Обчисліть:

1) ; 2) ; 3) ; 4) .

4.3. Відомо, що , і . Обчисліть:

1) ; 2) ; 3) ; 4) .

4.4. Дослідити функцію на неперервність:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ; 12)

4.5. Дослідити функцію на неперервність на вказаному проміжку:

1) , [0; 10]; 2) , [2; 10].

4.6. Вказати точки розриву функції:

1) ; 2) ; 3) ;

4) ; 5) ; 6) у = tg x.

4.7. Знайти у загальному вигляді приріст функції:

1) у = 2х² – 1; 2) у = 3х + 2; 3) у = 3х² – 2х;

4) у = -х² – 3х; 5) у = х³; 6) у = 2х³ – 2х².

4.8. Знайти похідну функції за означенням:

1) у = с; 2) у = х²; 3) у = х;

4) ; 5) у = х³; 6) у = х⁶;

7) ; 8) ; 9) ;

10) 11) 12) ;

13) у = 2х + 5; 14) у = х² + х; 15) у = 3х – 10.

4.9. Знайти похідну функції (продиференціювати функцію):

1) у = х¹⁰; 2) ; 3) ;

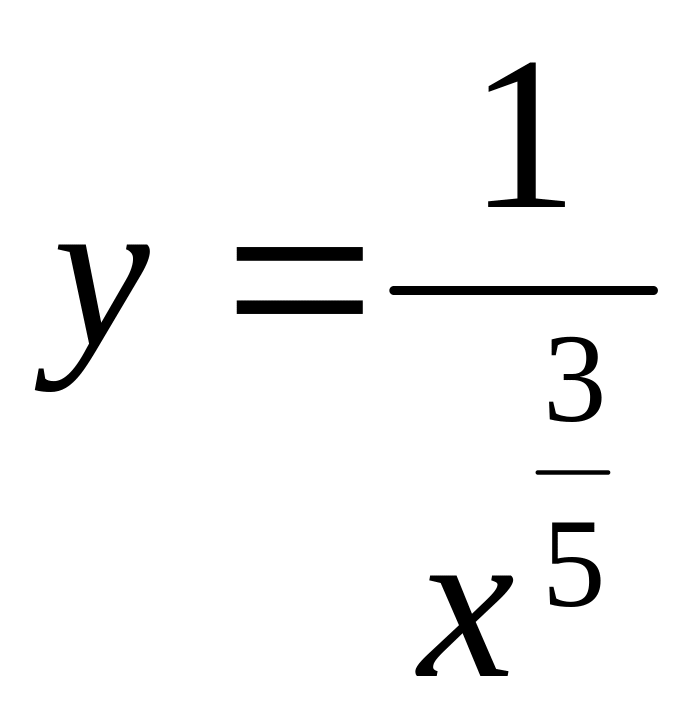4) у= х⁷; 5) ; 6) ;

7) ; 8) у = х² – 5; 9) у = х³ + 4х;

10) у = 5х²; 11) у = 4х³ – 10х² + 5х – 4; 12) ;

13) y = 3 + 2x³ + ; 14) ; 15) ;

16) y = 4 - + ; 17) ; 18) у = 3;

19) у = 5х³; 20) ; 21) ;

22) ; 23) ; 24) ;

25) ; 26) ; 27) y = (3 – 2х) ;

28) y = х ; 29) y = 4х³ - 6 - ; 30) ;

31) ; 32) ; 33) ;

34) у = -16х; 35) у = -8; 36) у = х² – 7х;

37) ; 38) ; 39) ;

40) ; 41) ; 42) ;

43) ; 44) ; 45) ;

46) ; 47) ; 48) ;

49) у = -8е^х; 50) у = 4 – е^2х; 51) у = х³ е^х;

52) ; 53) ; 54) y = 5e^x + 1;

55) ; 56) ; 57) ;

58) ; 59) ; 60) ;

61) ; 62) ; 63) ;

64) ; 65) ; 66) ;

67) ; 68) ; 69) ;

70) ; 71) ; 72) ;

73) ; 74) ; 75) ;

76) у = х¹⁰⁰; 77) ; 78) ;

79) ; 80) ; 81) у = -х⁵;

82) ; 83) y = ; 84) y = 3 · 2^x ;

85) y = - 3x² + 4e^{x +2}; 86) ; 87) ;

88) ; 89) ; 90) ;

91) ; 92) ; 93) ;

94) ; 95) y = cos x; 96) ;

97) ; 98) y = sin x; 99) ;

100) ; 101) y = (cos 3x + 6)³; 102) y = ;

103) y = (sin 2x - 5)³; 104) y = (1 - sin 2x)²; 105) ;

106) ; 107) ; 108) ;

109) ; 110) ; 111) ;

112) ; 113) ; 114) ;

115) ; 116) ; 117) ;

118) y = e^x sin x; 119) y = 7 cos 3x; 120) ;

121) ; 122) ; 123) ;

124) ; 125) ; 126) ;

127) ; 128) ; 129) ;

130) ; 131) ; 132) ;

133) ; 134) .