
- •Міністерство освіти і науки, молоді та спорту україни
- •Державний вищий навчальний заклад
- •«Бердичівський коледж промисловості, економіки та права»
- •Т.С.Волобуєва, н.А.Родер
- •Бердичів 2010 Волобуєва т.С., Родер н.А.
- •Тема 1. Функції, їх властивості і графіки
- •1.12. Обчислити: 1) ; 2) ; 3) ; 4) ;
- •1.17. Розв’яжіть рівняння:
- •1.18. Розв’язати нерівності:
- •Тестові завдання до теми
- •Тема 2. Тригонометричні функції
- •2.15. Знайти:
- •2.24. Розв’язати нерівності:
- •Тестові завдання до теми
- •Тема 3. Показникова та логарифмічна функції
- •3.1. Розв’язати рівняння:
- •3.12. Розв’язати нерівність:
- •3.13. Розв’язати систему рівнянь:
- •Тестові завдання до теми
- •Тема 4. Похідна та її застосування
- •4.1. Обчислити границі:
- •4.10. Знайти похідну другого та третього порядку:
- •4.11. Знайти значення похідної функції при заданому значенні аргумента (значення похідної в точці):
- •4.28. Обчислити швидкість зміни функції в точці х0:
- •4.73. Дослідити функцію та побудувати її графік:
- •Тестові завдання до теми
- •Тема 5. Інтеграл і його застосування
- •5.1. Для функції знайдіть хоча б одну первісну:
- •5.2. Знайти для функції первісну, графік якої проходить через дану точку:
- •5.3. Обчисліть невизначений інтеграл:
- •5.4. Обчисліть визначені інтеграли:
- •5.5. Знайти площу фігури, обмеженої лініями:
- •5.6. Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох фігури, що обмежена лініями:
- •5.7. Обчислити об’єм тіла, утвореного обертанням навколо вісі Оу фігури, що обмежена лініями:
- •Тестові завдання до теми
Тема 3. Показникова та логарифмічна функції
3.1. Розв’язати рівняння:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() ; 11)
; 11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ; 15)
; 15)
![]() ;
;
16)
![]() ; 17)
; 17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ; 21)
; 21)
![]() ;
;
22)
![]() ; 23)
; 23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ; 27)
; 27)
![]() ;
;
28)
![]() ; 29)
; 29)
![]() ; 30)
; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() ; 33)
; 33)
![]() ;
;
34)
![]() ; 35)
; 35)
![]() ; 36)
; 36)
![]() ;
;
37)
![]() ; 38)
; 38)
![]() ; 39)
; 39)
![]() ;
;
40)
![]() ; 41)
; 41)
![]() ; 42)
; 42)
![]() ;
;
43)
![]() ; 44)
; 44)
![]() ; 45)
; 45)
![]() ;
;
46)
![]() ; 47)
; 47)
![]() ; 48)
; 48)
![]() ;
;
49)
; 50)
![]() ; 51)
; 51)
![]() ;
;
52)
![]() ; 53)
; 53)
![]() ; 54)
; 54)
![]() ;
;
55)
![]() ; 56)
; 56)
![]() .
.
3.2. Розв’язати нерівність:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() ; 11)
; 11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ; 15)
; 15)
![]() ;
;
16)
![]() ; 17)
; 17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ; 21)
; 21)
![]() ;
;
22)
![]() ; 23)
; 23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ; 27)
; 27)
![]() ;
;
28)
![]() ; 29)
; 29)
![]() ; 30)
; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() ; 33)
; 33)
![]() ;
;
34)
![]() ; 35)
; 35)
![]() ; 36)
; 36)
![]() ;
;
37)
![]() ; 38)
; 38)
![]() .
.
3.3. Розв’язати систему рівнянь:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
3.4. Обчислити:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() ; 11)
; 11)
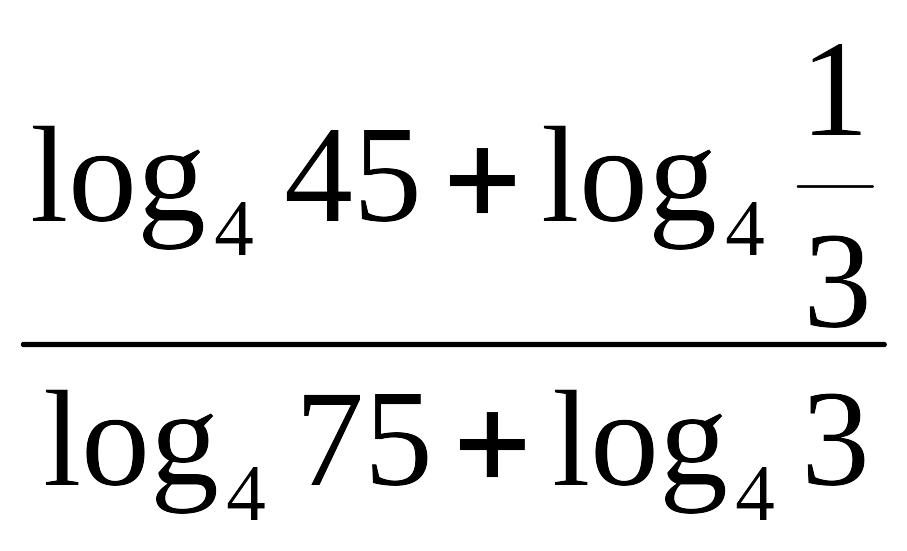 ; 12)
; 12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() ;
15)
;
15)
![]() ;
;
16)
![]() ;
17)
;
17)![]() ;
18)
;
18)![]() ;
;
19)
![]() ;
20)
;
20)
![]() ;
21)
;
21)
![]() ;
;
22)
![]() ;
23)
;
23)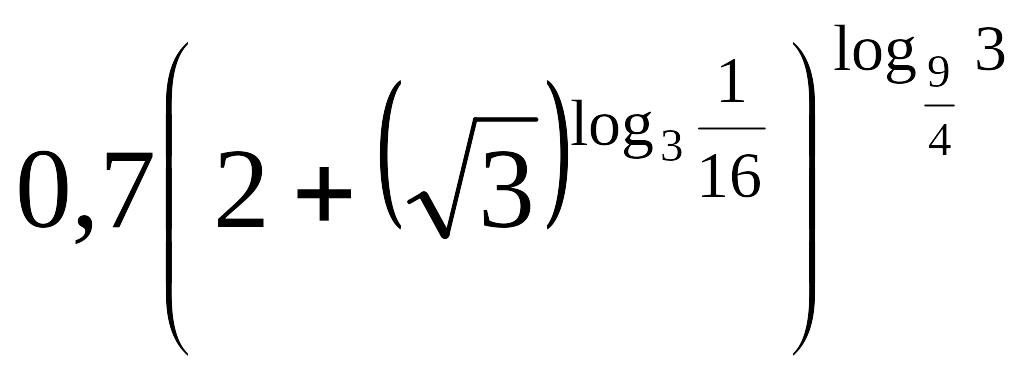 ;
24)
;
24)![]() ;
;
25)
![]() ; 26)
; 26)
![]() ; 27)
; 27)
![]() ;
;
28)
![]() ,
якщо
,
якщо
![]() ; 29)
; 29)
![]() ,
якщо
,
якщо
![]() ; 30)
; 30)
![]() .
.
3.5. Знайти значення виразу:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
;
; 4)
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ; 22)
; 22)
![]() ;
;
23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ; 28)
; 28)
![]() ;
;
29)
![]() ; 30)
; 30)
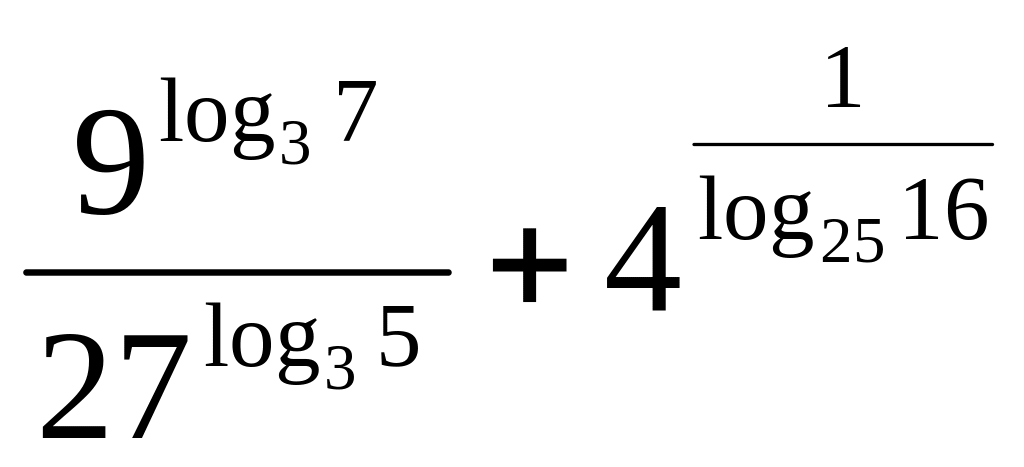 ;
;
31)
![]() ; 32)
; 32)
![]() ;
;
33)
![]() ; 34)
; 34)
![]() ;
;
35)
![]() ; 36)
; 36)
![]() ;
;
37)
 ; 38)
; 38)
![]() .
.
3.6. Прологарифмувати вираз:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
 ; 9)
; 9)
![]() .
.
3.7. Пропотенціювати вираз:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() .
.
3.8. Знайти корені рівнянь:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() .
.
3.9. Знайти область визначення функції:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() .
.
3.10. Знайти х, якщо відомо:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() .
.
3.11. Розв’язати рівняння
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)![]() ;
8)
;
8)![]() ;
;
9)![]() ;
10)
;
10)![]() ;
;
11)![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)![]() ;
15)
;
15)![]() ; 16)
а)
; 16)
а)![]() ;
;
17)![]() ;
18)
;
18)![]() ;
;
19) log 2 (x-1) = 3; 20) log 3 (x+1) = log 3 (2x+5) ;
21) ; 22) lg (x+2) = 1+lg x;
23)
![]() =2; 24)
;
=2; 24)
;
25) log
5
4 +
![]() (2x-3) = 1; 26)
log 3
(3x+1) = -1;
(2x-3) = 1; 26)
log 3
(3x+1) = -1;
27) log 3 (1-x) = log 3 (2x); 28) log 2 (x+1)- log 2 5x=1;
29) log
2 (log
3 (х-3))=1; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() (3x+1) +log 2
(х+15) = 2;
(3x+1) +log 2
(х+15) = 2;
33)
![]() (3x+2) = -2; 34)
log 8
8x - log 8
0,5 =
(3x+2) = -2; 34)
log 8
8x - log 8
0,5 =
![]() ;
;
35) log
2
3x +
![]() =
=![]() ; 36)
log 5
(х+7) - log 5
6= log 5
3;
; 36)
log 5
(х+7) - log 5
6= log 5
3;
37) log 2 (x+3) = log 2 5x + log 2 7; 38) log 5 х + (1-x) = 3;
39) log 3 (х+3)² = 4; 40) log 3 (х+8) = log 3 (0,5х+5);
40) log 0,2 (x – 2) = 1; 42) log 3 (4x+1) - log 3 (x+2) = 1;
43) log
2
(x-1) + log 2
5 = log 2
15; 44)
![]() ;
;
45) log
3
(2х-1)
+
![]() (x-1) = 1; 46)
log 4
(2х+1)²
= 3;
(x-1) = 1; 46)
log 4
(2х+1)²
= 3;
47) log 3 (3x-5) = log 3 (x-3); 48) log 2 (4-3x) = 4;
49) log 22 (x+5) + log 22 (2x+3) = 1; 50) log 2 (2x-1) + log 2 5x = 1;
51) log 3 (2x-1) + (х-1) = 1; 52) log 0,2 (х²+4х) = -1;
53) log
![]() (х-2)4
= 8; 54)
log 2
(2x-3) = log 2
(3x-5);
(х-2)4
= 8; 54)
log 2
(2x-3) = log 2
(3x-5);
55)
![]() (2x-6) = -2; 56)
log 3
2 + log 3
(x-2) = log 3
(x+1);
(2x-6) = -2; 56)
log 3
2 + log 3
(x-2) = log 3
(x+1);
57) log 2 x+ 3 = log 2 (x²+5х); 58) log 2 x + (1-х) = 3;
59) log
0,5 (х²-3х)
= -2; 60)
![]() (х+3)4
= 4;
(х+3)4
= 4;
61) ; 62) ;
63) ; 64) ;
65)
![]() ; 66)
; 66)
![]() ;
;
67)
![]() ; 68)
; 68)
![]() ;
;
69)
![]() ; 70)
; 70)
![]() ;
;
71)
![]() ; 72)
; 72)
![]() .
.
