§ 22. Пространственная система сил

Система сил называется пространственной, если линии действия сил, приложенных к телу, не лежат в одной плоскости. Подобно плоской системе пространственную систему сил можно привести к любой точке пространства. Порядок приведения тот же, что и для плоской системы сил, при этом от каждой силы в центре приведения получаем силу и пару сил.

Геометрическая сумма всех сил данной пространственной системы называется главным вектором. Модуль главного вектора определится через проекции на координатные оси х, у и z всех сил системы

R = 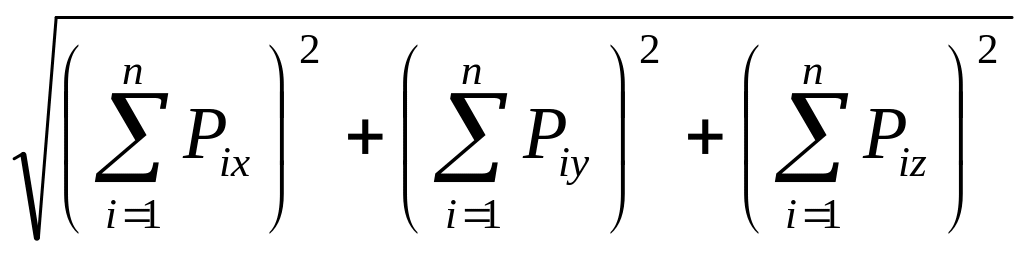. (26)

В отличие от плоской системы сил моменты сил пространственной системы относительно точки приведения действуют в разных плоскостях. Поэтому главный момент пространственной системы сил определяется как геометрическая сумма моментов всех сил относительно точки приведения.

Абсолютная величина главного момента заданной системы сил относительно некоторой точки определяется по формуле

M = 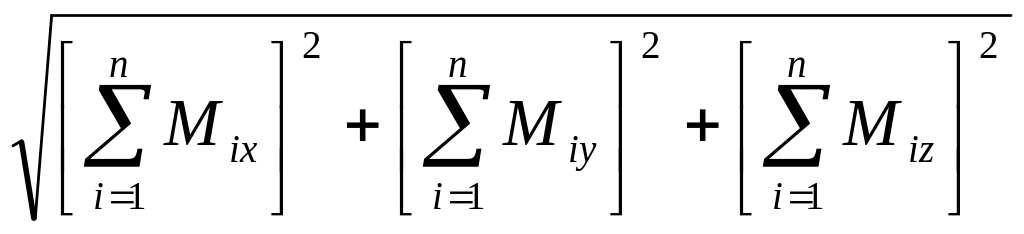, (27)

где , , – алгебраические суммы моментов всех сил системы относительно осей х, у, z, проходящих через рассматриваемую точку.

Равновесие пространственной системы сил имеет место, когда главный вектор и главный момент равны нулю, т.е.

R = 0; M = 0. (28)

На этом основании можно написать шесть уравнений равновесия:

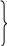= 0; = 0; =0

= 0; = 0; = 0. (29)

Глава V Центр тяжести. Геометрические характеристики плоских сечений

§ 23. Центр параллельных сил и его координаты

Любое тело можно рассматривать как состоящее из большого числа малых частиц, на которые действуют силы тяжести. Все эти силы направлены к центру Земли по радиусу. Так как размеры тел, с которыми приходится иметь дело в технике, ничтожно малы по сравнению с радиусом Земли (величина его около 6370 км), то можно считать, что приложенные к частицам силы тяжести параллельны и вертикальны. Следовательно, силы тяжести отдельных частиц тела образуют систему параллельных сил. Равнодействующую этих сил называют силой тяжести.

Установим одно важное свойство точки приложения равнодействующей двух параллельных сил. Пусть в точках А и В на тело действуют параллельные силы и (рис. 23, а). Равнодействующая этих сил равна их сумме, параллельна им, направлена в ту же сторону, а ее линия действия делит прямую АВ на части, обратно пропорциональные этим силам (см. § 21), т.е.

= .

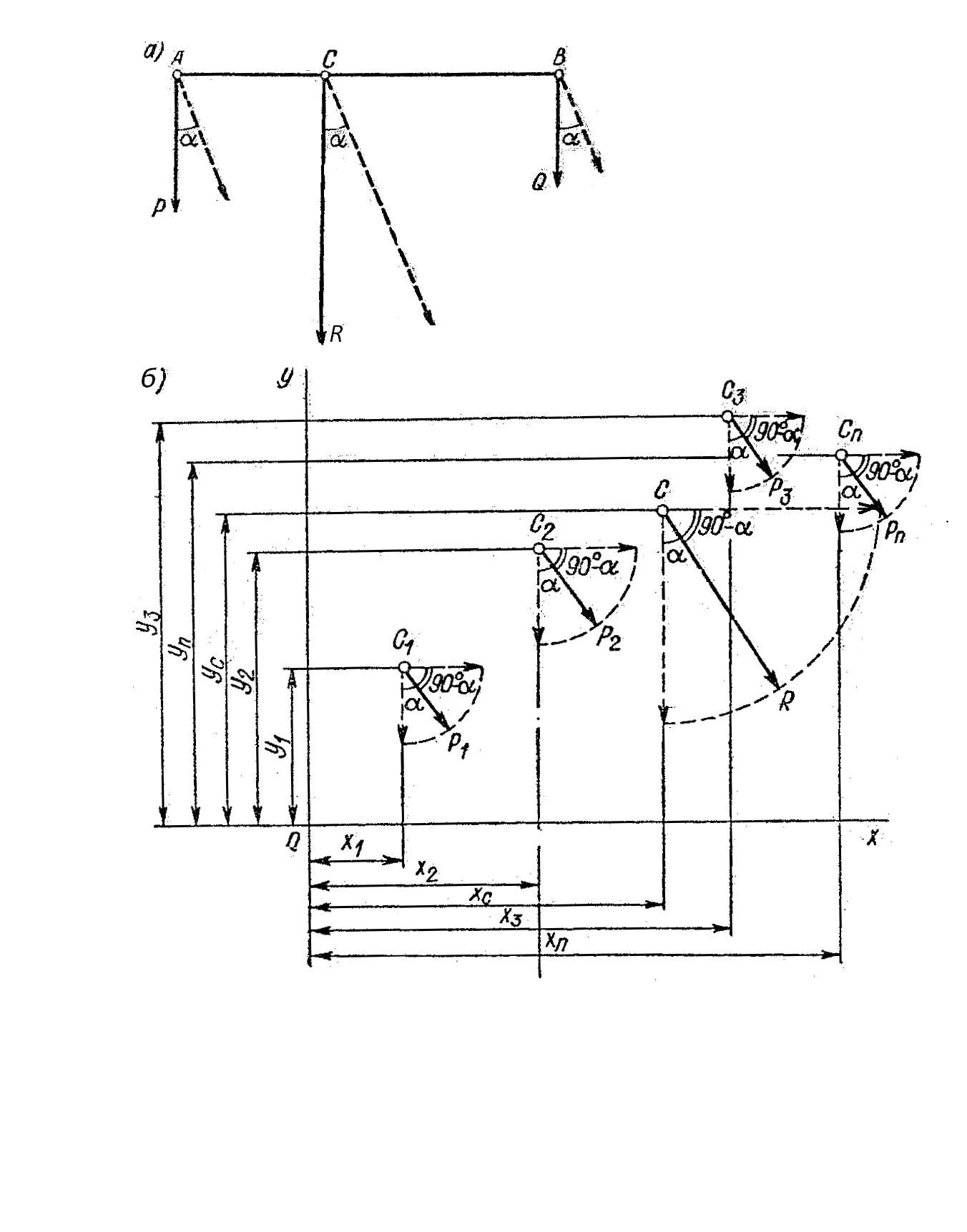
Рис. 23

Повернем силы P и Q на произвольный угол α, т.е. изменим их направление, сохранив параллельность. При этом равнодействующая останется равной их сумме, параллельно им, направленной в ту же сторону, а линия ее действия опять поделит прямую АВ на части, обратно пропорциональные величинам заданных сил. На рис. 23, а точкой О обозначено пересечение линии действия равнодействующей с линией АВ, соединяющих точки приложения составляющих сил. Эта точка называется центром параллельных сил, и ее положение не зависит от направления слагаемых сил.

Центр параллельных сил тяжести, действующих на все частицы тела, называется центром тяжести тела. Так как центр параллельных сил остается неизменным независимо от направления сил, то центр тяжести тела не меняет своего положения при повороте тела.

Выведем формулы, позволяющие определить положение центра любой системы параллельных сил. Пусть задана система параллельных сил , , …, ; координаты точек , , …, приложения этих сил известны (рис. 23, б). Обозначим точку приложения равнодействующей буквой С, а координаты этой точки, являющейся центром заданных параллельных сил, обозначим х_с, у_с. Как известно из предыдущего,

R = + + + …+ = . (30)

Если среди заданных параллельных сил имеются силы противоположных направлений, то они будут иметь разные знаки. Иными словами, нужно какое-либо направление принять за положительное и модули сил, совпадающих с этим направлением, подставлять в формулу (30) со знаком плюс, а модули сил противоположного направления – со знаком минус.

Так как положение центра параллельных сил не зависит от их направления, повернем все заданные силы на угол α по часовой стрелке так, чтобы они стали параллельны оси у (рис. 23, б). Равнодействующая при этом также повернется на угол α в ту же сторону.

Применим теорему о моменте равнодействующей (теорему Вариньона) относительно начала координат (точки О) с учетом правила знака моментов:

= = ,

откуда, умножив обе части уравнения на минус 1, получим

= = ,

но так как R = + + + …+ = ,

то = = .

Поворачивая по аналогии заданные силы против часовой стрелки на угол (90⁰-α) так, чтобы они стали параллельны оси х, и пользуясь теоремой о моменте равнодействующей, получаем аналогичную формулу для другой координаты центра параллельных сил:

= = .

Положение (координаты) центра пространственной системы параллельных сил определяют по формулам:

= ; = ; = . (31)

Приведенные формулы используют при вычислении координат центра тяжести тела, причем под P_i подразумевают силы тяжести отдельных частей тела, а под х_i, y_i, z_i – координаты их центров тяжести.

Наличие осей симметрии в однородном теле облегчает определение положения его центра тяжести.

Центр тяжести симметричного тела лежит в плоскости симметрии.

Плоскостью симметрии называют плоскость, разделяющую тело так, что каждой материальной точке, находящейся по одну сторону плоскости, соответствует равная ей по массе точка по другую сторону, причем линия, соединяющая эти точки, перпендикулярна плоскости симметрии и делится ею пополам.

На этом основании центр тяжести отрезка прямой линии находится в его середине. Центр тяжести плоской симметричной фигуры – тонкой однородной пластинки – лежит на оси симметрии, т.е. на линии уу, делящей фигуру на две равные части.

В однородном теле вес каждой отдельной части пропорционален ее объему V_i, т.е.

P_i= γ V_i,

где γ – удельный вес (постоянная величина для однородного тела).

В общих формулах (31), вынося γ за знак суммы в числителе и знаменателе и производя сокращение, получаем формулы для определения координат центра тяжести однородного тела или, как принято говорить, центра тяжести объема:

= ; = ; = , (32)

где V_i – объемы отдельных частей тела; х_i, y_i, z_i – координаты центров тяжести этих частей.

Например, центр тяжести призмы и цилиндра лежит на середине линии, соединяющей центры тяжести оснований. Центр тяжести шара совпадает с его геометрическим центром. Центр тяжести пирамиды лежит на прямой, соединяющей центр тяжести площади основания с противолежащей вершиной на расстоянии ¼ высоты от основания (рис. 24, а). Центр тяжести конуса лежит на прямой, соединяющей центр основания с вершиной на расстоянии ¼ высоты от основания (рис. 24, б).

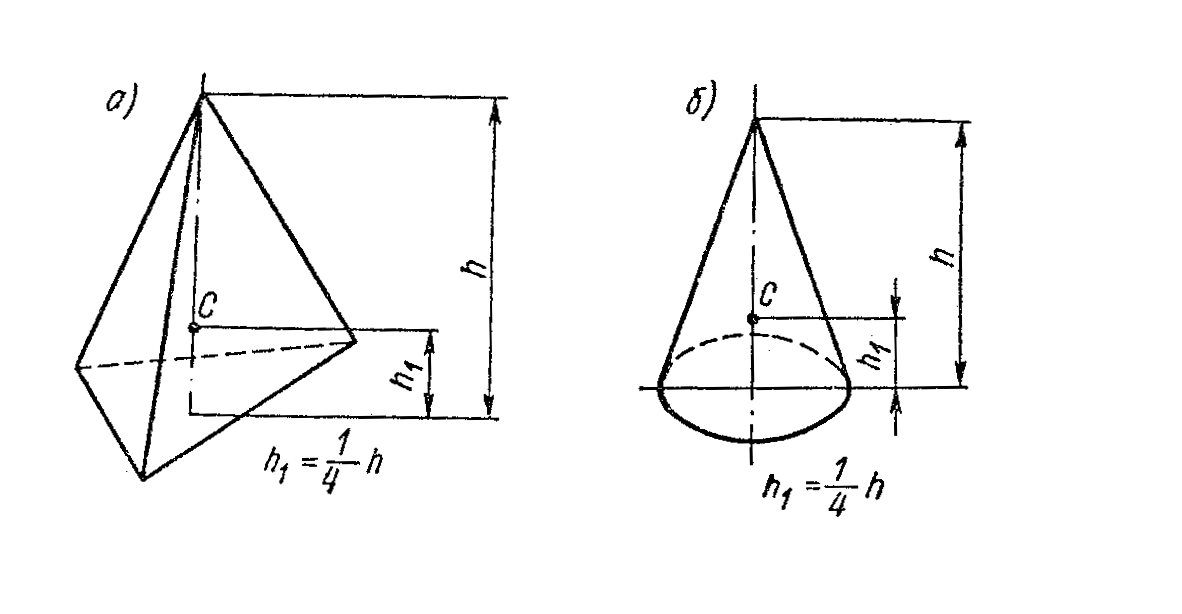
Рис. 24