
- •Введение
- •1. Асинхронный двигатель как объект управления
- •1.1.1. Понятие обобщённого пространственного вектора
- •1.1.2. Потокосцепления электрической машины
- •1.1.3. Уравнения статора и ротора в векторной форме
- •1.1.4. Обобщённая электрическая машина
- •1.2 Асинхронный короткозамкнутый двигатель
- •1.2.1 Уравнения короткозамкнутого АД
- •Эта функция имеет экстремумы при скольжении
- •1.2.4.1 Круговая диаграмма АД при питании от источника тока
- •1.2.4.2 Токи намагничивания и ротора
- •1.2.4.3 Электромагнитный момент
- •1.2.6 Модель АД при импульсном питании.
- •2. Частотное управление асинхронным двигателем
- •2.1. Модульное управление
- •Ток статора
- •Вид нагрузки
- •Закон
- •2.1.3.2 Управление с постоянным критическим моментом
- •2.1.4 Замкнутые системы частотного управления
- •2.2. Векторное управление
- •2.2.1 Трансвекторное управление (FOC)
- •2.2.1.2 Модель АД, управляемого током статора
- •2.2.1.3. Модель АД, управляемого напряжением статора
- •2.2.1.5. Особенности настройки регулятора скорости
- •2.2.2. Прямое управление моментом (DTC)
- •2.3 Преобразователи частоты для асинхронного электропривода
- •2.3.1 Основные типы преобразователей
- •2.3.2 Широтно-импульсные преобразователи
- •2.3.2.3 Пространственно-векторная модуляция
- •2.3.3.1 Подключение преобразователя
- •2.3.3.2. Основные характеристики и функции
- •Приложение 1.
- •Основное свойство симметричных m-фазных систем
- •Приложение 2.
- •Обобщённый вектор в симметричной m–фазной системе
- •Приложение 3.
- •Приложение 4.

Обобщённая электрическая машина |
17 |
m = 3 z C Im |
a b |
= 3 z C (a b − a b ). |
|||||
|
|
|
|
* |
|
|
|
|
2 |
p |
|
|
2 |
p |
m n n m |
|
|
|
|
|
|
||
Например, в произвольной системе координат электромагнитный момент определяется через потокосцепление и ток ротора в виде
m=−32 zp (ψ2m + jψ2n )×(i2m + ji2n )=−32 zp (ψ2mi2n −ψ2ni2m )= 32 zp (ψ2ni2m −ψ2mi2n )
1.2Асинхронный короткозамкнутый двигатель
1.2.1 Уравнения короткозамкнутого АД
Из уравнений статора и ротора обобщённой электрической машины (1.18) легко получаются уравнения асинхронного короткозамкнутого двигателя (АД) в произвольной системе координат, если положить u2 = 0
u |
(mn) |
= r i |
(mn) |
+ |
dψ(mn) |
(mn) |
ψ |
(mn) |
; |
||
|
|
|
1 |
+ jω |
|
|
|||||
1 |
1 1 |
|
dt |
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
0 |
= r |
i(mn) |
+ dψ(2mn) |
+ j ω(mn) −ω |
ψ(mn) |
||||||
|
2 2 |
|
dt |
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
|
|
||
Эти уравнения удобно использовать для анализа процессов в АД, если выбрать систему координат, вращающуюся синхронно с магнитным полем, т.е.
ω(mn) = ω . Тогда |
ω(mn) − ω= ω |
2 |
и уравнения АД в синхронной системе координат |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy принимают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
( xy) |
= r i |
( xy) |
+ |
dψ( xy) |
+ jω ψ |
( xy) |
; |
|||||
|
|
|
|
1 |
|
|||||||||
|
1 |
|
|
1 1 |
|
dt |
|
1 |
1 |
(1.20) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 = r i( xy) + dψ(2xy) |
|
|
|
|
|
||||||||
|
+ jω |
ψ( xy) |
|
|||||||||||
|
|
|
2 2 |
|
|
dt |
|
2 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дополняя эти уравнения тем или иным уравнением электромагнитного момента, можно анализировать процесс преобразования энергии в АД.
1.2.2 Статические характеристики АД при питании от источника напряжения
Уравнения Кирхгофа для статического режима АД можно получить как частный случай из уравнений АД в синхронной системе координат (1.20), используя уравнения потокосцеплений статора и ротора (1.14), представленные через основное потокосцепление ψm и потокосцепления рассеяния статора ψ1σ и ротора ψ2σ–
ψ1 = L1σi1 + Lmim = ψ1σ + ψm ; . ψ2 = L2σi2 + Lmim = ψ2σ + ψm
Учитывая, что в статическом режиме в синхронной системе координат dψ1 / dt = dψ2 / dt = 0 , а также то, что ω2 = sω1 , получим
18 |
|
|
Статические характеристики АД при питании от источника напряжения |
||||||||||||
u1 = i1r1 + jω1ψ1 = i1 (r1 + jω1L1σ )+ im jω1Lm = i1 (r1 + jx1σ )+ im jxm |
|
, |
|||||||||||||
0 = i r |
+ jω ψ |
2 |
= i |
2 |
(r |
+ jsω L |
)+ i |
m |
jsω L = i |
2 |
(r + jsx |
)+ i |
jsx |
||
2 2 |
2 |
|
2 |
1 2σ |
|
1 m |
2 |
2σ |
|
m m |
|
||||
где x1σ = ω1L1σ |
и x2σ = ω1L2σ – индуктивные сопротивления рассеяния при частоте |
||||||||||||||
статора ω1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разделим уравнение ротора на скольжение s , тогда |
|
|
|
|
|||||||||||
|
|
|
|
|
|
u1 = i1 (r1 + jx1σ )+ jim xm ; |
|
|
|
|
|
(1.21) |
|||
|
|
|
|
|
|
0 = i2 (r2 / s + jx2σ )+ jim xm |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Величина im xm равна |
|||
|
|
|
|
|
|
|
|
|
|
ЭДС, создаваемой основ- |
|||||
|
|
|
|
|
|
|
|
|
|
ным |
магнитным |
потоком |
|||
|
|
|
|
|
|
|
|
|
|
e1 = −e2 = jim xm , |
поэтому |
||||
|
|
|
|
|
|
|
|
|
|
уравнения |
(1.21) |
можно |
|||
|
|
|
|
|
|
|
|
|
|
представить в виде |
|
||||
|
|
|
|
|
|
|
|
|
|
u1 = i1r1 + ji1x1σ + e1 . |
(1.22) |
||||
|
|
|
|
|
|
|
|
|
|
e2 = i2r2 / s + ji2 x2σ |
|
||||
Уравнения (1.21-1.22) яв-
ляются традиционными уравнениями и их можно
представить двумя графиче-
Рис. 1.7. Схема замещения и векторная диаграмма АД скими формами – схемой
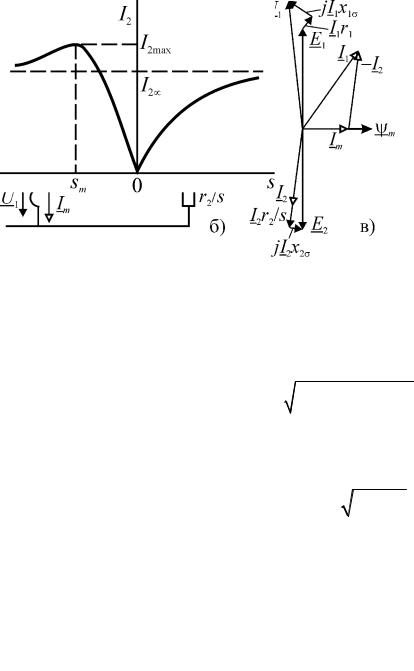
замещения и векторной диаграммой (рис. 1.7). Обычно для упрощения вычислений без внесения существенной погрешности ветвь намагничивания выносят на вход схемы замещения (рис. 1.7 б). Тогда ток ротора будет равен
I2 |
= |
U1 |
|
(1.23) |
(r + r / s)2 |
|
|||
|
|
+ x2 |
||
|
|
1 2 |
к |
|
где xк = x1σ + x2σ – индуктивное сопротивление короткого замыкания.
При возрастании скольжения ( s → ±∞) ток ротора стремится к величине
Рис. 1.8. Изменения тока ротора под нагрузкой
I2∞ = |
|
U1 |
|
(рис. 1.8). В генераторном ре- |
|||||||
|
r2 |
|
|
||||||||
|
|
|
+ x2 |
|
|
|
|
|
|||
|
|
1 |
|
к |
|
|
|
|
|
||
жиме |
|
функция |
I2 (s) |
имеет |
максимум |
||||||
I |
2 max |
= U1 |
при s |
m |
= −r |
/ r . |
|
|
|||
|
|
xк |
|
|
|
2 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Приравнивая активную мощность, пере- |
||||||||||
даваемую |
|
через |
зазор |
ротору |
двигателя |
||||||
|
2 |
|
m U 2r / s |
|
|
||||
P2 = m1I2 r2 / s = |
|
1 |
1 |
2 |
|
, |
электромаг- |
||
(r |
+ r |
/ s)2 |
+ x2 |
||||||
|
1 |
2 |
|
к |
|
|
|||
нитной |
мощности |
|
Pэм = M Ω1 , |
где |
|||||
Статические характеристики АД при питании от источника напряжения |
19 |
Ω1 =ω1 / zp = 2πf1 / zp , получим уравнение статической механической характеристики (рис. 1.9 а)
|
|
m z U 2r |
|
|
|
|
|
M = |
|
|
1 p 1 2 |
|
|
. |
(1.24) |
ω s (r |
+ r / s)2 |
+ x2 |
|
||||
|
1 |
1 |
2 |
к |
|
|
|
Эта функция имеет экстремумы при скольжении
sк = ± |
r2 |
|
r1 |
→0 |
r2 |
(1.25) |
|
|
|
|
→± |
|
|||
r2 |
|
|
xк |
||||
|
+ x2 |
|
|
||||
|
1 |
|
к |
|
|
|
|
называемом критическим, т.к. при этом скольжении АД переходит на статически неустойчивый участок характеристики или, как говорят, «опрокидывается». Использование приближенного равенства для критического скольжения не вносит существенной погрешности в анализ, т.к. у АД общего применения r1 = xк .
Подставляя (1.25) в (1.24), получим выражение для критического момента
|
|
|
|
|
|
|
m z U 2 |
|
r →0 |
m z U |
2 |
|
|
||
|
|
|
|
|
|
Mк = ± |
|
1 |
p 1 |
|
1 p 1 |
. |
(1.26) |
||
|
|
|
|
|
|
|
|
|
|
→± |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
± |
2 |
2 |
|
2ω1xк |
|
|
|
|
|
|
|
|
|
|
2ω1 r1 |
r1 |
+ xк |
|
|
|
|
||
|
Критический |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
момент |
в |
двигатель- |
|
|
|
|
|
|
|
|
|
|
|||
ном режиме опреде- |
|
|
|
|
|
|
|
|
|
|
|||||
ляет |
перегрузочную |
|
|
|
|
|
|
|
|
|
|
||||
способность |
АД, а |
|
|
|
|
|
|
|
|
|
|
||||
т.к. его значение за- |
|
|
|
|
|
|
|
|
|
|
|||||
висит |
от |
|
квадрата |
|
|
|
|
|
|
|
|
|
|
||
приложенного |
на- |
|
|
|
|
|
|
|
|
|
|
||||
пряжения, |
|
то |
при |
|
|
|
|
|
|
|
|
|
|
||
снижении |
|
напряже- |
|
|
|
|
|
|
|
|
|
|
|||
ния |
на |
допустимые |
|
|
|
|
|
|
|
|
|
|
|||
ГОСТом |
10%, |
мо- |
|
|
|
|
|
|
|
|
|
|
|||
мент уменьшится на |
Рис. 1.9. Механическая (а) и электромеханическая (б) |
||||||||||||||
20% |
и |
это |
следует |
||||||||||||
учитывать при выбо- |
|
|
|
|
характеристики АД |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
ре двигателя. В справочных данных для АД обязательно приводится коэффициент
перегрузочной |
способности соответствующий номинальному |
напряжению |
λ = Mк / Mном . |
Отсюда предельно допустимый момент |
будет равен |
M доп = (U1min /U1ном )2 λM ном . |
|
|
Положительный знак в (1.26) соответствует двигательному режиму, а отрицательный – генераторному. Поэтому в генераторном режиме критический момент больше, чем в двигательном. Отношение критических моментов определяется величиной r1 и равно
M |
кг |
|
r + |
r2 |
+ x2 |
r1 |
→ |
0 |
|
1 |
1 |
к |
|
||||
Mкд |
= |
r − |
r2 |
+ x2 |
→1 |
|||
|
|
1 |
1 |
к |
|
|
|
|
|
|
|
|
|
||||

20 |
Статические характеристики АД при питании от источника напряжения |
Для двигателей серии 4А в зависимости от мощности составляет от 3,0 до 1,3, причем, меньшие значения соответствуют большей мощности.
Делением выражения (1.24) на (1.26) можно получить уравнение механической характеристики АД в виде формулы Клосса
M = |
|
2Mк(1+ asк) |
r1→0 |
2Mк |
|
|
|
||||||
|
|
|
|
|
→ |
|
|
|
|
, |
(1.27) |
||
|
s |
+ |
s |
+ 2as |
s |
+ |
s |
|
|||||
|
|
|
к |
|
|
|
к |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sк |
|
s |
к |
|
|
sк |
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где a = r1 / r2 . Использование приближенного выражения, соответствующего условию r1 ≈ 0 , приводит к погрешности около 10-15% в двигательном режиме для машин с критическим скольжением sк = 0,15K 0,3 .
Из выражения (1.27) следует, что в области малых скольжений ( s = sк ) M = 2Mкs / sк , и характеристика близка к линейной, а при s ? sк – M = 2Mкsк / s ,
и характеристика практически гиперболическая.
Короткозамкнутые АД обычно запускаются прямым включением в сеть и развивают при этом момент
m z U 2r
Mп = ω1 (r11+pr2 )12 2+ xк2 .
Для получения высокого КПД АД должны работать при номинальной нагрузке с малым скольжением. Это требование вступает в противоречие с требованием получения достаточно высокого пускового момента. Из (1.27) при s =1 и s = sном
можно получить выражение для кратности пускового момента в виде
k |
|
= |
M |
п |
= |
s |
/ s |
+ s |
/ s |
s2 |
||||
п |
|
|
ном |
к |
|
к |
ном ≈ |
к . |
||||||
|
|
M |
ном |
|
|
1/ s |
|
+ s |
|
s |
|
|||
|
|
|
|
|
|
к |
|
к |
ном |
|||||
Для АД с номинальным скольжением 0,03 и критическим 0,1 эта кратность составит 0,36, т.е. такой двигатель может запускаться только на холостом ходу или при работе на вентиляторную нагрузку. По ГОСТ кратность пускового момента должна быть не менее 0,7–1,8. Причем, меньшие значения относятся к двигателям большей мощности. Повышение пускового момента АД достигается использованием явления вытеснения тока в стержнях ротора, в результате чего, кратность пускового момента повышается до 1,1–2,3.
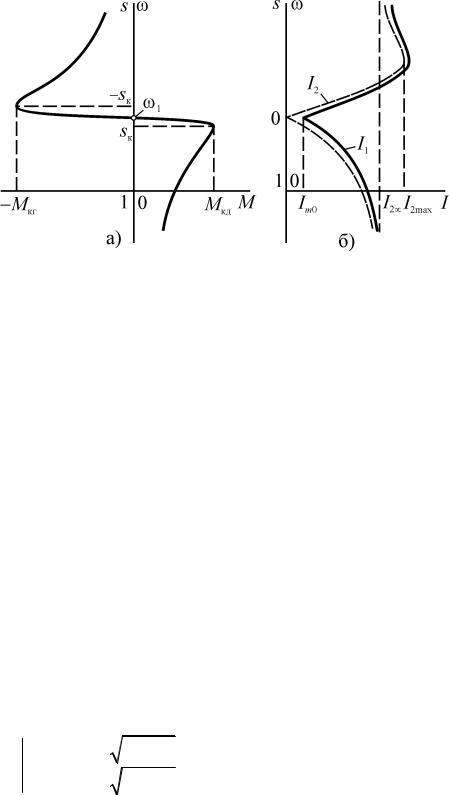
Другую проблему создают большие пусковые токи. Электромеханическая характеристика АД показана на рис. 1.9 б. Зависимость ω= F (I2 ) получена из вы-
ражения (1.23) и соотношения ω = ω1(1 − s) . Функция ω = F (I1) по характеру соответствует ω= F (I2 ) , т.к. токи статора и ротора связаны отношением i1 = im − i2 . Наибольшее отклонение ω = F (I1) от ω = F (I2 ) наблюдается в режиме холостого
хода, а по мере увеличения нагрузки кривые токов статора и ротора сближаются. В соответствии со стандартом, кратность пускового тока по отношению к номинальному не должна превышать 5,5-7,0. Однако эти значения могут быть недопустимо большими для питающей сети, особенно, если речь идет о машинах большой мощности. В этом случае для регулируемых приводов с преобразовате-

Статические характеристики АД при питании от источника напряжения |
21 |
лями частоты используют пуск с постепенным увеличением частоты питания, а для нерегулируемых – устройства «мягкого» пуска на основе тиристорных регуляторов тока с системой импульсно-фазового управления.
1.2.3 Динамические характеристики АД при питании от источника напряжения
Основой для анализа динамических свойств АД могут служить векторные уравнения статора и ротора в синхронной системе координат xy
u |
= i r |
+ dψ1 + jω ψ ; |
0 |
= i r |
+ dψ2 + jω |
ψ |
2 |
(1.28) |
||||
1 |
1 1 |
dt |
1 |
1 |
|
2 |
2 |
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и уравнение электромагнитного момента, представленного через потокосцепления статора и ротора*
|
|
|
|
|
|
|
|
|
|
m = |
3 z |
|
k1k2 |
(ψ |
|
×ψ ) = |
3 z |
|
|
k1k2 |
(ψ |
|
|
|
ψ |
−ψ |
|
ψ |
) . |
(1.29) |
||||||||||
|
|
|
|
|
|
|
|
|
|
p σL |
|
p σL |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
1 |
2 |
|
|
|
|
2 x |
|
|
1y |
|
2 y |
1x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим |
|
|
токи |
статора |
и |
|
|
|
|
ротора |
|
|
|
через |
потокосцепления |
|||||||||||||||||||||||||
i1 = (ψ1 − k2ψ2 ) /(σL1); |
i2 = (ψ2 − k1ψ1) /(σL2 ) |
|
и, подставив в уравнения (1.28), запи- |
|||||||||||||||||||||||||||||||||||||
шем их в форме Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
dψ1 |
|
|
|
1 |
|
|
|
′ |
|
|
|
|
|
|
′ |
|
dψ2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
′ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= T2′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
dt |
= T1′(u1T1 + k2ψ2 −ψ1 − jω1T1ψ1 ); |
|
dt |
|
(k1ψ1 −ψ2 − jω2T2ψ2 ) |
(1.30) |
||||||||||||||||||||||||||||||||||
где T1′= L1′/ r1 |
и T2′ = L2′ / r1 |
– переходные постоянные времени статора и ротора, в |
||||||||||||||||||||||||||||||||||||||
которых |
|
|
|
|
|
|
|
|
|
L1′ = L1σ + L2σLm /(L2σ + Lm ) = σL1 = L1σ + k2 L2σ ≈ L1σ + L2σ = Lк |
и |
|||||||||||||||||||||||||||||
L2′ = L2σ + L1σLm /(L1σ + Lm ) = σL2 = L2σ + k1L1σ ≈ L2σ + L1σ = Lк |
|
т.н. переходные ин- |
||||||||||||||||||||||||||||||||||||||
дуктивности соответствующие электрическим цепям рис. 1.10. |
|
|
||||||||||||||||||||||||||||||||||||||
Совместим вектор |
напряжения |
статора |
|
|
с |
|
|
осью x |
системы координат |
|||||||||||||||||||||||||||||||
(u1x =U1m ; u1y = 0 ). Тогда, разделяя в (1.30) проекции векторов, получим |
|
|||||||||||||||||||||||||||||||||||||||
dψ |
|
|
|
|
1 |
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
|
dψ1y |
|
|
1 |
|
|
|
|
|
′ |
|
||||||||||
1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||
dt |
|
|
T1′ |
(u1xT1 + k2ψ2x −ψ1x +ω1T1ψ1y ); |
|
dt |
|
|
|
T1′ |
(k2ψ2 y −ψ1y −ω1T1ψ1x ); |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.31) |
||||||||||||
dψ2x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
dψ2 y |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
||||||||||||||
|
|
= |
|
|
|
|
|
(k1ψ1x −ψ2x +ω2T2ψ2 y ); |
|
|
|
|
|
= |
|
|
|
|
(k1ψ1y −ψ2 y +ω2T2ψ2x ); |
|
||||||||||||||||||||
dt |
|
|
T2′ |
dt |
|
|
T2′ |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
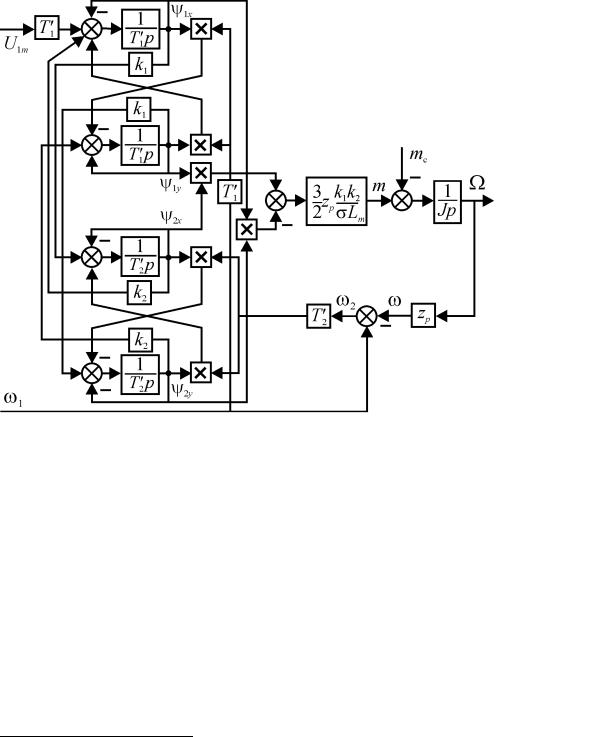
Уравнения (1.29) и (1.31) можно представить в виде структурной схемы, показанной на рисунке 1.11. Она имеет два входа, соответствующих управляющим воздействиям по напряжению и частоте статора. Принципиально можно ограничится воздействием на АД только по одному из входов, установив на другом заданное постоянное значение. В этом случае мы получим управление двигателем с
помощью изменения напряжения питания Рис. 1.10. Электрические цепи,
соответствующие переходным индуктивностям статора (а) и ротора (б)
* См. таблицу 1.1 раздела 1.1.4
22 |
Динамические характеристики АД при питании от источника напряжения |
или частоты статора. Однако управление изменением напряжения при глубоком регулировании обладает очень низкими энергетическими показателями и в современном приводе применяется крайне редко и только для машин малой мощности. Управление изменением частоты при постоянном напряжении питания применяется только для регулирования скорости вращения вверх от номинальной. Чаще всего для обеспечения оптимальных условий протекания процессов преобразования энергии в АД между входами управления устанавливают функциональный
преобразователь, создающий определенную связь между напряжением и частотой*.
Рис. 1.11. Структурная схема АД, управляемого напряжением и частотой статора.
При питании от источника напряжения ( u1 = const ) потокосцепление статора ψ1 изменяется незначительно, в основном из-за падения напряжения на активном сопротивлении r1 , и в синхронной системе координат можно считать, что dψ1 / dt ≈ 0 . Если принять также r1 ≈ 0 , то из уравнения статора (1.28) с учётом того, что система координат ориентирована по вектору напряжения u1 , получим
ψ = − j |
u1 |
|
ψ |
|
= 0; ψ |
= −U |
1m |
/ ω |
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||||
1 |
|
|
ω1 |
|
|
1x |
|
|
1y |
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и тогда электромагнитный момент будет равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m = 3 z |
|
k1k2 |
ψ |
ψ |
|
= 3 z |
|
k1k2 |
|
− |
U1m |
|
ψ |
|
. |
(1.32) |
||||||
p |
|
2 x |
p |
|
|
|
2 x |
|||||||||||||||
2 |
σLm |
1y |
|
|
2 |
|
|
|
|
ω1 |
|
|
|
|
||||||||
|
|
|
|
|
|
σLm |
|
|
|
|
|
|
|
|||||||||
* См. далее раздел 2.1.2
Динамические характеристики АД при питании от источника напряжения |
23 |
Заменим производную в уравнении ротора (1.28) оператором Лапласа и разделим проекции векторов, получим
′ |
′ |
|
|
T2 pψ2x +ψ2x −ω2T2ψ2 y = 0 |
. |
(1.33) |
|
′ |
′ |
||
T2 pψ2 y + ψ2 y + ω2T2ψ2x = k1ψ1y |
|
|
|
Отсюда ψ2 y = ψ2x 1 +T2′p . Подставляя это выражение во второе уравнение,
ω2T2′
определим искомое значение ψ2 x
ψ2 x = |
|
k1ψ1y |
|
. |
(1.34) |
|
|
1 |
+T2′p |
|
|||
|
(1 +T2′p) |
+ω2T2′ |
|
|||
|
|
ω2T2′ |
|
|||
В этом выражении дальнейшие алгебраические преобразования невозможны, т.к. первый оператор дифференцирования в знаменателе относится ко всей дроби (1 +T2′p) / ω2T2′, где ω2 (t) Ђ ω2 ( p) в общем случае является функцией времени.
Заметим, что переходная постоянная времени ротора равна
|
T2′ = σT2 = |
|
(1− k1k2 )L2 |
= |
L1L2 − L2m |
= |
L2σ + k1L1σ |
≈ |
|
Lк |
= |
|
xк |
≈ |
|
1 |
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r2ω1ном |
|
|
|
|||||||||||||||||||||||
где: Lк = L1σ + L2σ |
|
r2 |
|
|
|
|
r2L1 |
|
|
|
|
r2 |
|
r2 |
|
sкω1ном |
||||||||||||||||||||||
– индуктивность короткого замыкания, а sк = r2 / xк |
– прибли- |
|||||||||||||||||||||||||||||||||||||
женное значение критического скольжения. Если произведение ω2T2′ представить |
||||||||||||||||||||||||||||||||||||||
как |
ω2 |
|
= |
|
β |
, где β = |
|
ω2 |
|
– относительная частота ротора или абсолютное |
||||||||||||||||||||||||||||
ω |
s |
|
|
|
ω |
|||||||||||||||||||||||||||||||||
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1ном |
к |
|
|
|
к |
|
|
|
|
1ном |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
скольжение, то из (1.34) мы получим |
|
|
|
|
k1 (−U1m / ω1 ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ψ2 x = |
|
|
|
|
|
k1ψ1y |
|
|
|
|
= |
|
|
|
|
|
|
. |
|
|
(1.35) |
||||||||||||||||
|
|
|
|
|
sк |
|
|
|
|
|
|
β |
|
|
sк |
|
|
|
|
|
β |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(1 +T2′p) |
|
|
(1 +T2′p) |
+ |
|
|
|
|
(1 +T2′p) |
|
(1 |
+T2′p) |
+ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
β |
|
s |
|
|
|
β |
s |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
||||||
После чего из (1.32) с учетом (1.35) можно получить уравнение динамической механической характеристики
|
|
|
|
|
|
|
|
|
|
m = |
|
|
|
|
|
2Mк |
|
|
|
|
, |
(1.36) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
β |
|||||
|
|
|
|
|
|
|
|
|
|
|
(1+T2′p) |
β (1+T2′p) |
+ s |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
||
где M |
|
= |
3 z |
|
k1k2 |
|
− |
U1m |
2 k ≈ |
3 z |
|
U1 |
2 |
1 |
. |
|
|
|
|
|
|
||
к |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
4 |
|
|
ω1 |
|
1 |
2 |
p |
|
Lк |
|
|
|
|
|
|
||||||
|
|
|
|
σLm |
|
|
|
ω1 |
|
|
|
|
|
|
|
|
|||||||
Выражения (1.33) и (1.36) позволяют построить структурную схему АД, управляемого напряжением и частотой статора при условии ψ1 ≈ const или, что то
же самое, при r1 = 0 (рис. 1.12).
Уравнение (1.36) отражает влияние электромагнитных процессов в АД на электромеханические. При p = 0 оно преобразуется в уравнение статической ме-
ханической характеристики (1.26). Уравнение нелинейно, но для малых прираще-
24 |
Динамические характеристики АД при питании от источника напряжения |
ний на рабочем участке механической характеристики его можно линеаризовать. Для этого вначале выполним дифференцирование
|
|
|
|
Рис. 1.12. Структурная схема АД при условии ψ1≈const. |
|
|
|
|||||||||||
′ |
2 d |
2 |
m |
′ dm |
|
|
β |
2 |
|
′ |
2 1 dβ dm |
′ |
1 dβ |
|
β |
|
||
|
|
|
|
m = 2Mк |
|
|||||||||||||
|
|
|
+ |
|
|
|
|
|
|
, |
||||||||
(T2 ) |
dt2 |
+ 2T2 |
dt |
+ m 1 |
s |
|
|
+(T2 ) |
β dt dt |
−T2 |
β dt |
s |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
к |
|
||
а затем разложим результат в ряд Тейлора в окрестности точки M 0 , β0 . Пренебре-
гая членами ряда высшего порядка, после преобразований представим уравнение механической характеристики в приращениях в виде
′ |
2 d 2∆M |
′ |
d∆M |
|
β |
|
2 |
|
2M |
к |
s2 |
−β2 |
′ |
|
s2 |
d∆β |
||||
|
|
|
+ |
|
0 |
|
|
= |
|
|
к |
0 |
|
к |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
(T2 ) |
dt2 |
+ 2T2 |
dt |
+ ∆M 1 |
s |
|
|
s |
|
s2 |
+β2 |
∆β+T2 |
s2 |
+β2 |
dt |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
к |
|
|
к |
|
к |
0 |
|
к |
0 |
|
|||||
Это уравнение позволяет анализировать |
электромеханические |
процессы в |
||||||||||||||||||
любой точке статической механической характеристики. Однако для АД наибольший интерес представляет рабочий участок характеристики при s < sк . Тогда,
полагая |
M0 = 0 и β0 = 0 , соответственно ∆M = m − M 0 = m и ∆β = β −β0 =β, по- |
|||||||||
лучим |
|
|
|
|
|
|
|
|
2Mк |
|
|
|
|
|
2 |
|
2 |
|
|
β(1+T2′p) (1+T2′p)m = hU (ω1 −ω) , |
|
|
m |
(T2′) |
|
p |
|
+ 2T2′p +1 |
= |
s |
||
|
2Mк |
|
|
|
|
|
|
к |
|
|
где hU = |
= 2MкT2′ |
|
|
(1.37) |
||||||
ω |
s |
|
|
|||||||
|
1ном к |
|
|
|
|
|
|
|
|
|
– модуль жесткости линеаризованной механической характеристики.
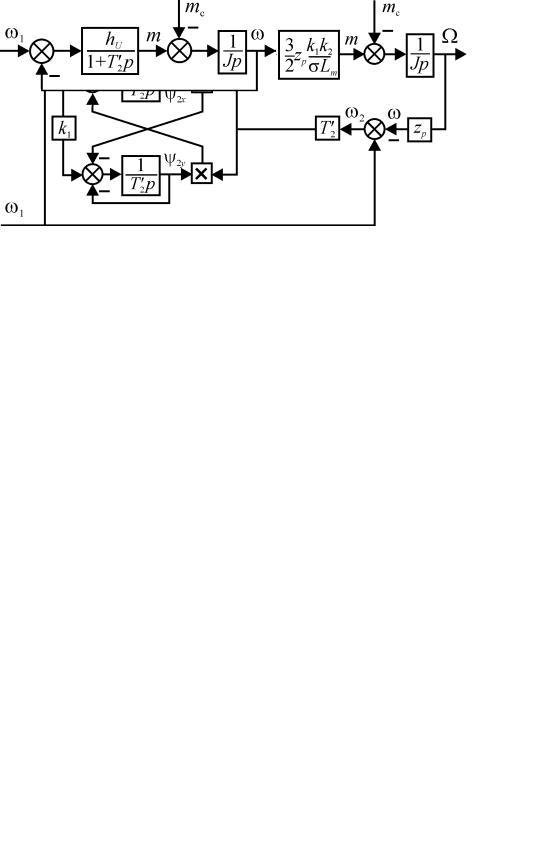
Таким образом, на рабочем участке механической характеристики АД можно представить звеном первого порядка (рис. 1.13) с передаточной функцией дина-
мической жесткости |
|
|
|
|
|
h ( p) = m( p) |
= − |
hU |
|
|
|
|
|
||||
д |
ω( p) |
1+T2′p |
|
||
|
|
||||
Постоянная времени T2′ двигателей |
|
||||
общего применения составляет величину |
|
||||
Рис. 1.13. Структурная схема АД для |
|||||
5…50 мс и меньшие значения соответству- |
рабочего участка механической |
||||
ют двигателям малой мощности |
характеристики |
||||
