§ 2. Распределение Гаусса

Распределение Гаусса является предельным случаем распределения Пуассона и многих других законов распределения.

Рассмотрим распределение Пуассона при больших n₀ и n. Дискретность распределения по n в этом случае теряет свое значение, так как n меняется практически непрерывно. Будем характеризовать отличие n от n₀ с помощью ε, определенного соотношением

n = n₀(1 + ε).

Подставляя формулу Стерлинга

в выражение (П.2), найдем:

_,

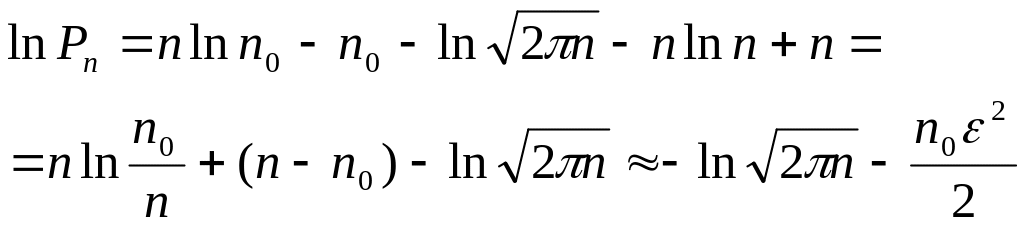откуда

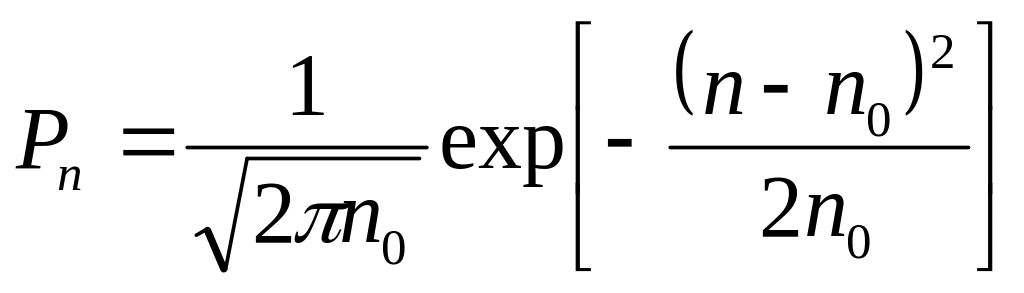. (П.4)

Вероятность P_n может быть обобщена на непрерывные величины. Чтобы это сделать, заметим, что n – n₀ равно отклонению найденной на опыте величины n от среднего значения n₀. Обозначим это отклонение через x:

x = n – n₀.

Заменим n₀ стандартным отклонением σ с помощью (П.3). Наконец, заметим, что P_n можно интерпретировать как вероятность того, что найденное на опыте значение n лежит в интервале между n – ½ и n + ½. Этому интервалу соответствует Δx = 1. Произведя указанные замены и перейдя от обозначения P_n к обозначению P(x), получим:

. (П.5)

Распределение (П.5) носит название распределения Гаусса. P(x) определяет вероятность того, что величина x попадает в единичный интервал Δx, окружающий точку х. Выбирая вместо единичного бесконечно малый интервал dx, найдем:

. (П.6)

Ф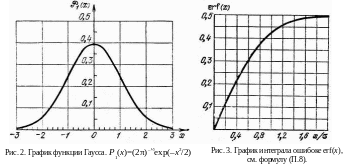 ормула (П.6) определяет вероятность того, что для x будет найдено значение, заключенное между x–½dx и x+½dx. Величина P(x) называется плотностью вероятности. График функции P₁(x), т. е. P(x) при σ = 1, изображен на рис. 2.

С помощью (П.6) нетрудно найти вероятность того, что для x будет найдено значение, лежащее между x₁ и x₂, где x₁ и x₂ – любые числа. Как нетрудно понять,

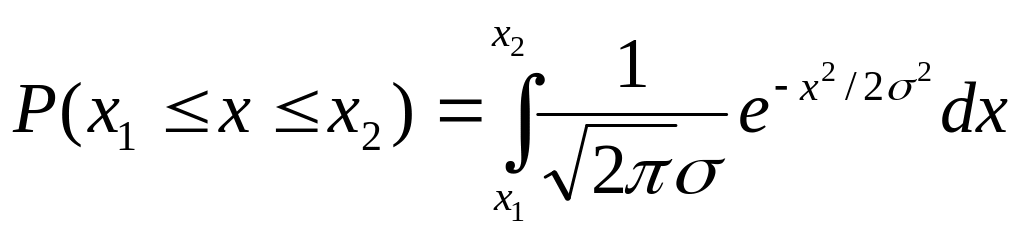. (П.7)

Интеграл (П.7) в элементарных функциях не выражается. Он может быть вычислен с помощью таблиц интеграла вероятности erf(x):

. (П.8)

Нетрудно показать, что

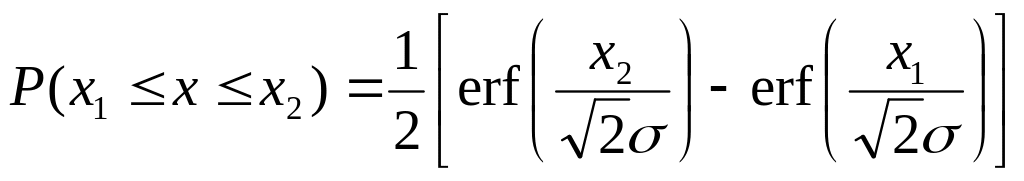. (П.9)

График функции erf(x) изображен на рис. 3. Функция erf(x) антисимметрична относительно точки x = 0, так что

erf(–x) = – erf(x). (П.10)

С помощью таблиц или графика erf(x) нетрудно найти вероятность того, что для искомой величины будет найдено значение, лежащее между –σ и σ, между –2σ и 2σ и между любыми другими значениями x:

_.

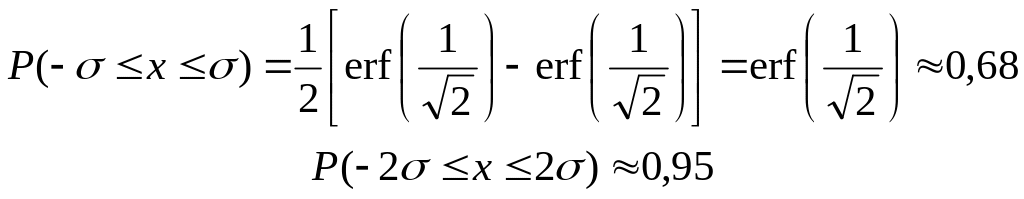Вероятность найти величину x в заданных пределах при увеличении ширины интервала быстро приближается к единице. Так.

,

и т. д. Из этого факта часто делается неверное утверждение о том, что погрешности, превосходящие 3σ, а тем более 4σ, практически никогда не встречаются. На самом деле они встречаются не так уж редко. Это происходит потому, что истинные распределения погрешностей очень разнообразны и никогда в точности не следуют закону Гаусса. Эти распределения обычно считают гауссовыми за неимением лучшего. В области малых отклонений от среднего закон распределения Гаусса по большей части неплохо оценивает вероятности различных встречающихся на практике отклонений, а в области больших отклонений описывает их плохо, и чем отклонения больше – тем хуже.