10.2 Выбор оптимальных параметров регуляторов

При заданной структуре САУ задача выбора параметров сводится к следующему. Необходимо отыскать такие значения изменяемых параметров, при которых квадратичная интегральная оценка становится минимальной.

В системе автоматического управления, которая исследуется в лабораторной работе, переменным параметрам является постоянная времени интегратора . Все другие постоянные времени и коэффициенты передачи заданы постоянными.

Следовательно, задача состоит в определении оптимального значения , при котором . В качестве управляющего устройства рассматриваются И– и ПИ – регуляторы.

Интегральная квадратичная оценка может быть определена по изображению ошибки

. (10.5)

Для практических целей более удобной является формула Релея, которая

получается из (10.5) заменой :

. (10.6)

Если подынтегральное выражение представить в виде

,

где

, (10.7)

, (10.8)

то интеграл (10.6) вычисляется по формуле

, (10.9)

, .

М етодический пример. Запишем изображения ошибки для И– и ПИ – регуляторов соответственно при :

И–регулятор: ;

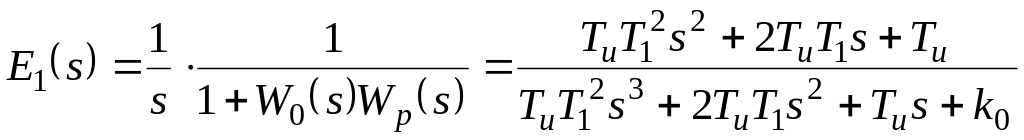ПИ–регулятор: .

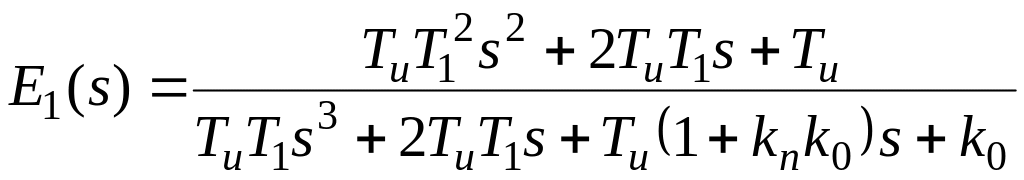Составим выражение для I в случае ПИ–регулятора. Определим полиномы и согласно уравнениям (10.7) и (10.8):

; (10.10)

; (10.11)

Из выражений (2.10) и (2.11) найдем коэффициенты и :

, , ,

, , .

При подстановке данных коэффициентов в (10.9) получим выражение интегральной квадратичной оценки

ПИ–регулятор: 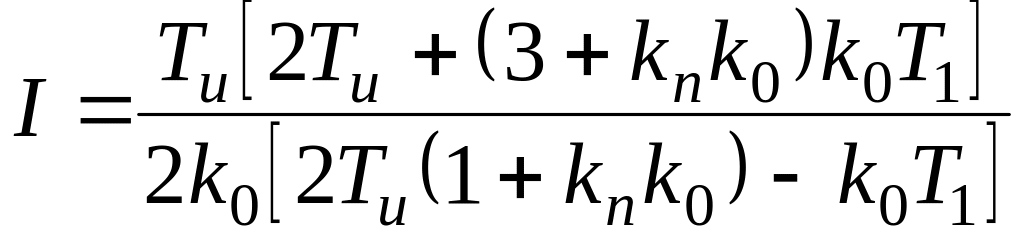. (10.12)

Выражение для в случае И–регулятора получается из (10.12), как частный случай подстановкой

И–регулятор: (10.13)

Искомое значение , при котором , найдем, дифференцируя (10.12) и (10.13) по и приравнивая производную нулю:

ПИ–регулятора: , (10.14)

И–регулятор: . (10.15)

При схемотехнической и программной реализации рассмотренных регуляторов удобнее пользоваться коэффициентом передачи интегрирующего блока .

Исходя из выражений (10.14) и (10.15), получим значение оптимального коэффициента передачи интегрирующего блока

ПИ–регулятор: ,

И–регулятор: .

10.3 Порядок выполнения работы

1. Собрать схему моделирования линейной САУ (рисунок 10.1). В качестве объекта управления использовать передаточные функции из таблицы 7.1. Параметры задать в соответствии с данными таблицы 10.1.

Таблица 10.1 – Исходные данные

Тип регулятора	Параметры регуляторов
	kП	kИ	k0
П	0.051	0	10
И	0	0.0510	1
ПИ	1	0.0510	1

2. Рассчитать область возможных значений коэффициента передачи интегрирующего блока k_И, при которых выполняется условие устойчивости САУ. Расчет выполнить отдельно для И– и ПИ – регуляторов с учетом приведенных в таблице параметров. Для П–регулятора рассчитать область возможных значений коэффициента передачи k_П.

3. Проверить экспериментально выполнение условий устойчивости для П–, И– и ПИ–регуляторов.

4. Для САУ с П – регулятором рассчитать установившуюся ошибку e_уст и построить график зависимости e_уст=f(k_П).

5. Снять экспериментальную зависимость e_уст=f(k_П) для САУ с П–регулятором. Сопоставить результаты эксперимента с расчетными данными. Пронаблюдать величину установившейся ошибки при использовании И – и ПИ–регуляторов.

6. Рассчитать оптимальные значения коэффициента передачи интегрирующего блока k_И для И– и ПИ–регуляторов. Проверить выполнение условия устойчивости при k_И= k_Иопт.

7. Определить экспериментально зависимость интегральной оценки от коэффициента передачи k_И и представить полученные результаты в виде графика .

8. Для САУ с И–, ПИ – регуляторами экспериментально исследовать переходный процесс. Определить величину перерегулирования и время переходного процесса при следующих значениях коэффициента передачи интегрирующего блока

1) k_И= 0.2k_Иопт; 2) k_И=k_Иопт; 3) k_И= 2k_Иопт.