3.3. Свойства функций, непрерывных на отрезке.

Определение. Функция называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала.

Функция называется непрерывной на отрезке , , если она непрерывна на интервале и при этом непрерывна в точке справа, а в точке слева.

Перечислим свойства функций, непрерывных на отрезке.

1. Если непрерывна на , то она достигает на этом отрезке своего наибольшего и наименьшего значения.

Это означает, что на найдутся такие точки и , что для всех , при этом  наибольшее, а  наименьшее значение на (рис.3.3).

2. Если функция непрерывна на и на концах его принимает значения разных знаков, то тогда найдётся по крайней мере одна точка внутри этого отрезка, в которой функция обращается в ноль: (рис.3.4).

3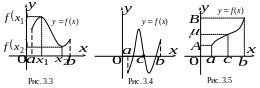 . Пусть функция непрерывна на отрезке , причём на его концах принимает разные значения и , . Тогда каково бы ни было число , заключенное между и , найдётся такая точка внутри , что (рис.3.5).

Глава 4 производная

4 .1. Понятие производной, её физический и геометрический смысл. Дифференциал функции.

Пусть функция определена в некоторой окрестности точки . Рассмотрим значения этой функции в двух близлежащих точках: исходной (фиксированной) и новой (переменной) , такой, что отрезок (или отрезок , если ) целиком лежит в области определения (рис.4.1).

Определение. Величина называется приращением аргумента в точке , а величина  приращением функции в точке . При этом может быть как положительным, так и отрицательным.

При фиксированном величина будет функцией .

Рассмотрим отношение .

Определение. Если существует предел отношения приращения функции в точке к приращению аргумента в этой же точке при , то такой предел называется производной функции в точке и обозначается или :

(4.1)

Функция, имеющая производную в точке , называется дифференцируемой в этой точке, а процесс отыскания производной называется дифференцированием.

Замечания:

1) В определении производной может быть как положительным, так и отрицательным;

2) зависит от точки , т.е. является функцией , поэтому в обозначении производной в качестве аргумента пишут , т.е. или ;

3) Можно показать, что если дифференцируема в точке , то она в ней непрерывна (обратное утверждение неверно).

Определение. Функция называется дифференцируемой на интервале , если она дифференцируема в любой точке этого интервала.

Пример 4.1. Пусть , тогда , т.е. для .

Пример 4.2. . Покажем, что в точке производная этой функции не существует. Рассмотрим выражение:

, т.е. это выражение при предела не имеет (см. замечание 1 к определению производной). Заметим что данная функция при дифференцируема, причём .

Физический смысл производной. Рассмотрим функцию , дифференцируемую в точке (рис. 4.1). Отношение является средней скоростью изменения этой функции на отрезке (или , если ). Тогда, согласно (4.1), представляет собой скорость изменения функции в точке (т.е. «мгновенную» скорость).

Пример 4.3. При свободном падении с нулевой начальной скоростью зависимость пути от времени выражается функцией , где . Найдём закон изменения скорости от времени при таком движении.

Поскольку, исходя из физического смысла производной , следует при любом фиксированном составить отношение и перейти к пределу при .

;

. Итак, установлено, что скорость увеличивается пропорционально времени . Так, например, в момент мгновенная скорость падения будет .

Геометрический смысл производной. Рассмотрим  секущую графика функции (рис.4.1), угловой коэффициент которой .

Определение. Касательной в точке к графику функции называется прямая, проходящая через и являющаяся предельным положением секущей при устремлении точки по графику к точке с любой стороны.

При этом , , , а угол между и касательной стремится к нулю.

В силу данного определения и определения производной

(4.2)

т.е. производная в точке является угловым коэффициентом касательной к графику функции в точке . Заметим, что если не дифференцируема при , то в соответствующей точке график этой функции не имеет касательной.

Согласно формуле (4.2), уравнение невертикальной касательной к графику функции в точке , где , имеет вид

(4.3)

Для невертикальной нормали к графику функции в точке (т.е. прямой, проходящей через перпендикулярно касательной) получим уравнение.

, (4.4)

Пусть имеет в точке производную . Зафиксируем эту точку и рассмотрим малое приращение в точке (рис.4.1). Согласно определению производной (4.1), а также свойству 1 бесконечно малых функций, можно записать:

, где при ,

т.е. бесконечно малая функция при , откуда получим

. (4.5)

Определение. Дифференциалом функции в точке называется главная часть её приращения в этой точке, линейная относительно :

. (4.6)

Если , то величина в выражении (4.5) является бесконечно малой высшего порядка по сравнению с главной частью приращения.

Дифференциал зависит как от самой точки , так и от приращения и в выражении (4.6) обычно заменяется переменной : .

Рассмотрим функцию вида . Поскольку при всех , как было показано в примере (4.1), то для такой функции , т.е.

(4.7)

Таким образом, дифференциал независимой переменной совпадает с её приращением. С учётом этого можно записать:

или (4.8)

Из формул (4.8), с учётом геометрического смысла производной (рис.4.1), ясен геометрический смысл дифференциала: в точке есть приращение ординаты касательной к графику функции в точке , соответствующее приращению аргумента .