2.3. Основные теоремы о пределах. Первый и второй замечательные пределы. Сравнение бесконечно малых.
Теорема 1. Предел суммы двух, трёх и вообще любого конечного числа функций равен сумме пределов этих функций при условии, что каждый из них существует, т.е.
(2.14)
Пример 2.10.
Теорема 2. Предел произведения двух, трёх и вообще любого конечного числа функций равен произведению пределов этих функций при условии, что каждый из них существует, т.е.
(2.15)
Следствие 1.
Постоянный множитель
можно выносить за знак
предела
Следствие 2.
Предел целой степени функции
равен степени предела этой функции:
Пример 2.11.
Теорема 3. Предел частного двух функций равен частному пределов этих функций при условии, что каждый из них существует и предел знаменателя отличен от нуля:
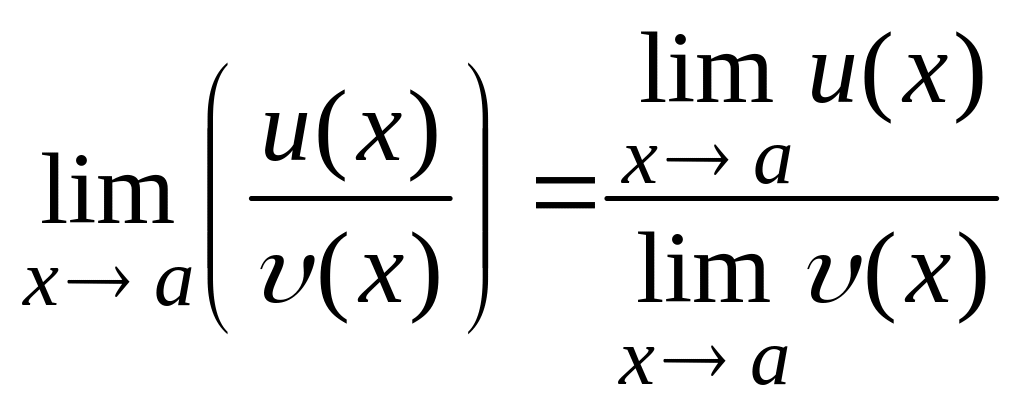при
(2.16)
Заметим, что
все сформулированные теоремы справедливы
и для последовательностей при
,
как для частного случая функций.
Пример 2.12.
Вычислить
исходный предел равен
.
При вычисление пределов непосредственное применение указанных теорем не всегда приводит к успеху. Тогда необходимо провести предварительные преобразования исходной функции.
Пример 2.13.
Вычислить
.
Непосредственное применение теоремы
о пределе частного невозможно, так как
предел знаменателя равен нулю. Однако,
возможно преобразование:
,
причем сокращение допустимо, поскольку
при вычислении предела сама точка
не рассматривается. Таким образом,
.
Пример 2.14.
Вычислить
.
Непосредственное применение теоремы
о пределах невозможно, поскольку ни
числитель, ни знаменатель предела не
имеют, а стремятся к бесконечности, т.е.
имеет место неопределённость типа
.
Применим преобразование:
,
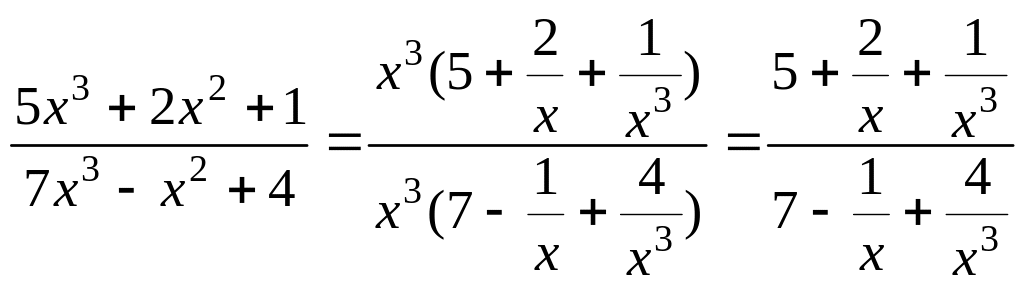после чего получим:
Рассмотрим некоторые важные пределы. Можно доказать, что:
,
.
Справедливо утверждение о том, что:
(2.18)
Этот предел называется первым замечательным пределом.
Следствие:
,
поскольку
Рассмотрим
последовательность
.
Можно доказать, что она имеет предел,
обозначаемый через
,
который выражается бесконечной
непериодической дробью:
(2.19)
и называется вторым замечательным пределом.
Можно показать,
что и для функции
,
справедливо:
. (2.20)
Если же в (2.20)
сделать замену переменной
,
то получим
, (2.21)
при этом строгое обоснование правомерности такой замены здесь приводить не будем.
Пример 2.15.
,
при этом
при
.
Здесь и далее замена переменной строго не обосновывается, но она достаточно понятна и иногда процесс подобного рода можно не выписывать, а проводить в уме.
Пример 2.16.
Вычислить
.
Решение:
.
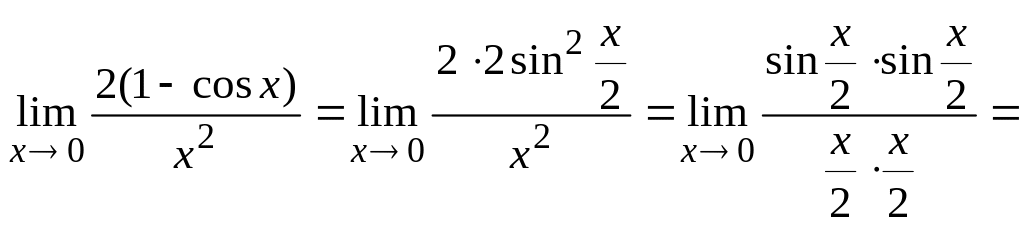
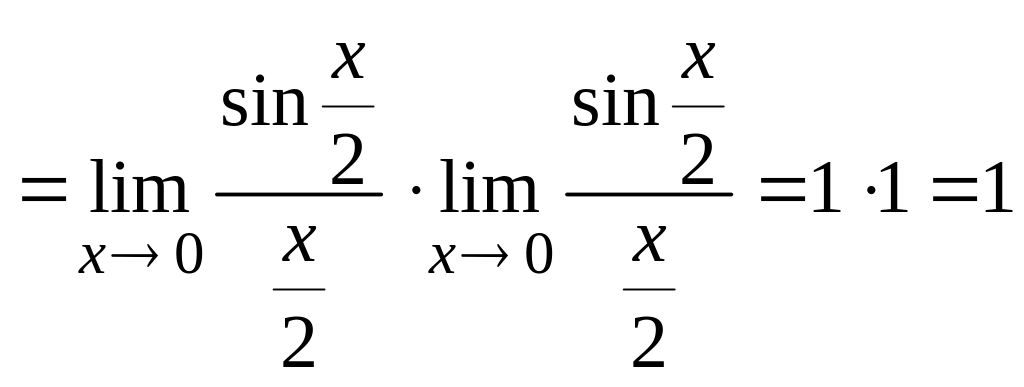Пример 2.17.
Вычислить
.
Решение:
.
Пример 2.18.
Вычислить
.
Решение:
,
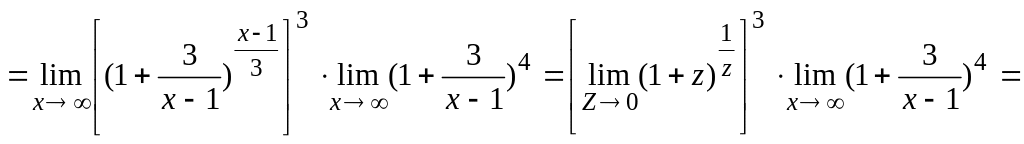
здесь произведена замена
при
.
Познакомившись
с числом
,
мы можем определить натуральный логарифм
по основанию
:
,
а также показательную функцию, называемую
экспонентой:
.
Сравнение бесконечно малых.
Пусть
и
бесконечно малые
функции при
.
Определение.
Функции
и
называются бесконечно малыми одного и
того же порядка малости при
,
если
существует и отличен от нуля.
Пример 2.19.
,
бесконечно малые
одного порядка при
,
т.к.
.
Определение.
и
называются эквивалентными бесконечно
малыми при
,
если
.
Эквивалентность
и
обозначается
символом
при
.
На основании приведённых выше примеров
и согласно определению первого
замечательного предела можно записать:
,
,
при
(2.22)
Определение.
называется бесконечно малой более
высокого порядка малости, чем
при
,
если
и более низкого порядка малости, чем
при
,
если
;
и называются несравнимыми бесконечно малыми при , если не существует.
Пример 2.20.
более
высокого порядка малости, чем
при
и, соответственно,
более низкого порядка, чем
при
,
поскольку
,
.
Пример 2.21.
и
несравнимые бесконечно малые при
,
поскольку
при
предела не имеет.
Теорема.
Пусть
,
при
и
существует. Тогда существует предел
отношения
,
причём
.
Пример 2.22.
,
т.к.
,
,
при
.
Теорема. Сумма конечного числа бесконечно малых при функций
различных порядков эквивалента слагаемому
самого низкого порядка.
Пример 2.23.
а)
при
б)
при
Пример 2.24.
Вычислить
Решение:
Числитель эквивалентен
,
а знаменатель эквивалентен
,
следовательно, искомый предел равен
.