1.4 Двенадцать повернутых на 900 планов скоростей

Сначала исследуется движение начальных звеньев, а затем выполняется кинематический анализ отдельных структурных групп в порядке их подсоединения к механизму I класса.

Планом скоростей (ускорений) звена называется графическое изображение, представляющее собой плоский пучок, лучи которого изображают абсолютные скорости (ускорения) точек звена плоского механизма, а отрезки, соединяющие концы лучей, - относительные скорости (ускорения) соответствующих точек при данном положении звена. Планом скоростей механизма называется совокупность планов скоростей звеньев механизма с одним общим полюсом.

План скоростей механизмов II класса строится в порядке, определяемом структурной группой механизма: определяют скорость точки входного звена (в большинстве случаев скорость конца кривошипа); выбирают масштабный коэффициент скоростей; определяют скорости точек диады, следующей за механизмом I класса, затем скорости точек других диад в порядке подсоединения структурных групп.

Каждая диада включат в себя три кинематические пары. Скорости внешних точек диады, либо известны, если они осуществляют подсоединение звена к стойке, либо могут быть определены предварительно, и поэтому могут быть выбраны за полюс при определении скорости внутренней точки диады. Для нее составляются два векторных уравнения, выражающих скорость внутренней точки через скорости внешних точек этой диады.

В полученных системах векторных уравнений скорости полюсов известны по модулю и направлению, поэтому подчеркиваются двумя линиями. Скорости относительного движения между точками по модулю неизвестны, но направление их можно определить, поэтому они подчеркиваются одной линией, и внизу указывается направление, соответствующее скорости.

Определяем угловую скорость конца кривошипа (точка А_1,2, рис.1) по формуле 1.4.1..

₁= n_кр/30 = 3,14*72/30= 7,54 с^-1 (1.4.1) с.68 [5]

где n_кр – число оборотов кривошипа, об/мин.

Определяем скорость конца кривошипа по формуле 1.4.2, допуская что ₁= const, то скорость точки А_1,2 для всех положений постоянна.

_

V_A1,2 = ₁*l_OA = 7,54 * 0,09 = 0,68 м/с (1.4.2) с.68 [5]

где l_OA – длина кривошипа, м.

После определения скорости, выбираем масштабный коэффициент _v.

м/с

мм

_

_v= V_A1,2 / [p_Va_1,2]= 0,68/ 68 = 0,01 (1.4.3) с 68 [5]

В выбранном масштабе откладываем отрезок [p_va₁₂] от полюса плана скоростей (произвольная точка р) перпендикулярно направлению кривошипа в сторону вращения ₁.

Скорость точки В равна нулю (V_B=0 м/с), так как эта точка принадлежит стойке. Далее определим скорость внутренней точки диады А_3. Для этого составим систему уравнений, где выразим ее скорость через скорости внешних точек.

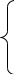_ _ _ (1.4.4) с.57 [4]

V _A3= V_A1,2 + V_A3A1

//СB

_ _ _

V_A3= V_В + V_A3В

=0 СВ

В этой системе в первом уравнении два неизвестных (скорость точки А₃ и относительная скорость V_A3A1). Второе уравнение превращается в тождество. Первое уравнение системы решается графически. Для этого проводим из конца вектора p_va₁₂ на плане скоростей прямую, параллельную направлению относительной скорости V_A3A1, т.е. параллельно звену СВ, а из полюса р прямую перпендикулярную звену СВ. Точка пересечения этих прямых и даст конец вектора p_Va₃, т.е. скорость точки А₃. Истинное значение скорости V_A3 определяется по формуле 1.4.5. _

V_A3= [p_Va₃ ]* _v (1.4.5) с.57 [4]

Значение скорости точки С определим методом подобия: точки на плане скоростей должны располагаться подобно точкам на звене. И т.к. точка С лежит на одном звене с точкой А₃, то по формуле 1.4.6 определим:

[p_Va₃] AB

[ p_Vc ] BC (1.4.6) с.57 [4]

Определив длину вектора p_Vc, откладываем ее на продолжении вектора p_Va₃ и полюса р. Причем необходимо учитывать, что в различных положениях механизма эта длина будет меняться. Истинное значение скорости V_C определяется аналогично скорости точки А₃ (формула 1.4.5).

Аналогично определению скорости внутренней точки А₃, определяем скорость внутренней точки D по формуле 1.4.7. Составляем систему, учитывая, что скорость точки Е равна нулю. (V_E=0 м/с).

_ _ _

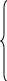V_D= V_E0 + V_DE0

=0 //DE

_ _ _ (1.4.7) с.57 [4]

V_D= V_C + V_A3В

СD

Решение системы, так же осуществляется графически. Из полюса р (скорость точки Е₀) проводится прямая параллельная направлению относительной скорости V_DE0, т.е. параллельно звену DE₀, а из конца вектора p_Vc прямая перпендикулярная звену CD.

На пересечении прямых получается искомая точка d. При соединении ее с полюсом получим вектор p_vd, характеризующий скорость точки D на плане скоростей. Истинное значение скорости V_D находится аналогично скорости точки А₃ (формула 1.4.5).

Значения величин относительных скоростей (V_A3A1,V_CD) находятся из плана скоростей, как произведения отрезков характеризующих относительные скорости ([cd], [a₁₂a₃]) на масштабный коэффициент плана скоростей _v.

Скорости центров тяжести (центры масс) находятся методом подобия. Точка s должна лежать на отрезке плана скоростей и делить его в таком отношении, в каком точка S делит соответствующее звено. Соединив полученную точку с полюсом, получим вектор ps, характеризующий скорость центра тяжести звена. Умножив полученную величину на масштабный коэффициент, получим истинное значение скорости центра масс звена.

Точка S₁ совпадает с полюсом, следовательно, V_S1=0 м/с. Точка S₅ принадлежит звену, совершающему поступательное движение, следовательно, скорости всех точек звена одинаковы и V_S5=V_D. Точка S₃ делит звено ВС пополам, отсюда длина вектора ps = 0,5 pc. Умножив полученную величину на масштабный коэффициент, получим истинную скорость V_S3.

Угловые скорости звеньев находятся как отношение относительной скорости между точками звена, на расстояние между этими точками по формуле 1.4.8.

₃= V_BC/l_BC (для третьего звена, причем V_BC=V_C)

₄= V_CD/l_CD (для четвертого звена) (1.4.8) с.57 [4]

Звенья 2 и 5 совершают поступательные движения и не имеют угловых скоростей.

Расчет скоростей для всех одиннадцати положений одинаковый, все уравнения остаются неизменными, только изменяются значения входящих в них величин. Поэтому приведем пример расчета для первого положения механизма:

– по формулам (1.4.1 – 1.4.3) найдена скорость конца кривошипа V_A12 и выбран масштабный коэффициент. Откладываем отрезок [p_va₁₂] от полюса плана скоростей р.

– решая графически систему (1.4.4) находим отрезок [p_Va₃], определяем его истинное значение по формуле (1.4.5)

V_A3= [p_Va₃]* _V= 31,6 * 0,01 = 0,316 м/с

–далее по свойству подобия (формула 1.4.6) находим величину отрезка [p_Vc ] на плане скоростей

[p_Vc ]= [p_Va₃]*ВС/ АВ= 31,6* 245/ 149,9= 51,6 мм

и его скорость (формула 1.4.5)

V_C= [p_Vc ]* _V= 51,6 * 0,01= 0,516 м/с

– решив графически систему (1.4.7), определяем скорость точки D

V_D= [p_Vd ]* _V= 49,16*0,01= 0,492 м/с

– определяем относительные скорости V_A3A1,V_CD, предварительно измерив отрезки [cd], [a₁₂a₃] на плане скоростей

V_A3A1= [a₁₂a₃]* _V= 60,21* 0,01= 0,602 м/с

V_CD= [cd]* _V= 15,23*0,01= 0,152 м/с

– определяем скорости центров масс звеньев

V_S1= 0 м/с

V_S3= 0,5 [p_Vc ]* _V= 0,5*51,6*0,01= 0,258 м/с

V_S5= V_D= 0,492 м/с

– определяем угловые скорости третьего и четвертого звеньев (формула 1.4.8)

₃= V_BC/l_BC = 0,516/0,49= 1,053 с^-1

₄= V_CD/l_CD = 0,152/ 0,2= 0,76 с^-1

Определив все величины, в каждом из положений механизма, заносим их значения в таблицы 1.1 и 1.2

Таблица 1.1 – Скорости точек звеньев

№пол. V,м/с	0		1	2	3	4	5	6	7	7’	8	9	10	11
[pVa12],мм	68
VA12	0,68
[pVa3], мм	0		31,6	53,8	65,8	67,4	58,4	39,3	10,3	0	26,1	59,7	65,4	37,3
VA3	0		0,32	0,54	0,66	0,67	0,58	0,39	0,1	0	0,26	0,6	0,65	0,37
[a12a3],мм	0		60,2	41,6	17,8	9,35	34,7	55,5	67,2	0	62,8	32,6	18,4	56,8
VA3A1	0		0,6	0,42	0,18	0,09	0,35	0,56	0,67	0	0,63	0,33	0,18	0,57
[pVc ], мм	0		51,6	78,5	90,6	92	83,4	61,8	18,8	0	57,5	156,	176	87,1
VC	0		0,52	0,78	0,9	0,92	0,83	0,62	0,19	0	0,58	1,56	1,76	0,87
[pVd ], мм	0		49,2	77,6	91	91,5	81,4	59,3	18	0	55	152,	177,	83,7
VD=VS5	0		0,49	0,78	0,91	0,92	0,81	0,59	0,18	0	0,55	1,52	1,77	0,84
[cd], мм	0		15,2	16	7,66	4,24	14,3	16,8	6,2	0	17,7	25	15,9	24,3
VCD	0		0,15	0,16	0,08	0,04	0,14	0,17	0,06	0	0,18	0,25	0,16	0,24
[pVs3],мм	0		25,8	39,2	45,3	46	41,8	30,9	9,4	0	28,8	77,9	88,1	43,6
VS3	0		0,26	0,39	0,45	0,46	0,42	0,31	0,09	0	0,29	0,78	0,88	0,44
VB=VE=VS1		0

Таблица 1.2 – Угловые скорости точек звеньев

№пол. , с-1	0	1		2		3		4	5		6			7		7’		8		9		10		11
1	7,54
3	0	1,05	1,6		1,85		1,88			1,7		1,26	0,38		0		1,17		3,18		3,59		1,78
4	0	0,76	0,8		0,38		0,21			0,72		0,84	0,31		0		0,89		1,25		0,79		1,22

Для построения повернутых планов скоростей необходимо готовый план повернуть вокруг полюса в любую сторону на 90⁰.