1.14.4. Формирование сопряженного базиса

Как и задача поиска для ЗЛП допустимого базиса, так и определение ее сопряженного базиса является в общем случае самостоятельной задачей. Однако практика применения двойственного симплекс-метода показала, что потребность в нем возникает, как правило, тогда, когда сопряженный базис очевиден. Рассмотрим кратко эти случаи.

Первый случай. Реализуются одновременно следующие условия выбора :

1) для , (1.111)

2) для . (1.112)

Действительно, на основе (1.111) имеем , и следовательно .

Проверяя условие сопряженности базиса с учетом (1.111, 1.112) и , видим его очевидное выполнение.

Конкретным примером реальной ЗЛП, где это выполняется, является задача о составлении оптимальной смеси (см. 1.1.2). После перехода к направлению оптимизации на max , изменения знака неравенства во всех ограничениях на противоположные (" ") и перехода к ограничениям типа равенства можно видеть, что базис, составленный из балансовых переменных будет по условиям (1.111), (1.112) сопряженным.

Два других случая связаны с исследовательскими задачами определения влияния корректировки параметров и структуры ЗЛП на ее решение.

Второй случай. Решена ЗЛП. Необходимо ответить на вопрос, как изменится решение задачи при вариации правой части некоторого ограничения. Решить эту задачу можно без повторного решения ЗЛП с самого начала следующим образом, используя заключительную симплекс-таблицу ( или ). Необходимо убедиться, что вариация правой части ограничения ЗЛП привела к изменению состава активных ограничений. Для этого осуществляется расчет скорректированного столбца базисных переменных и замена им прежнего :

. (1.113)

Признаком изменения состава активных ограничений является отрицательные элементы в этом столбце. Строка симплекс-разности, соответствующая , при этом не изменяется ( ), т.е. возникают условия сопряженности базиса: прежний можно считать начальным сопряженным базисом . Начиная с него, применяется алгоритм двойственного метода симплекс-таблиц. В результате его применения, как правило, за очень малое количество итераций либо будет получено новое оптимальное решение, либо установлено, что проведенная вариация ограничения (если она сужает D) привела к .

Третий случай

Решена ЗЛП. Необходимо ответить на вопрос, как изменится решение задачи при введении в структуру задачи нового, -ого ограничения типа неравенства. Решить эту задачу, как и предыдущую, можно без повторного решения ЗЛП с самого начала, также используя заключительные симплекс-таблицы или .

Подставим найденное оптимальное решение в новое ограничение и убедимся, что оно не выполняется (в противном случае дальше делать ничего не надо). После этого осуществляются следующие операции:

1. Новое ограничение с номером 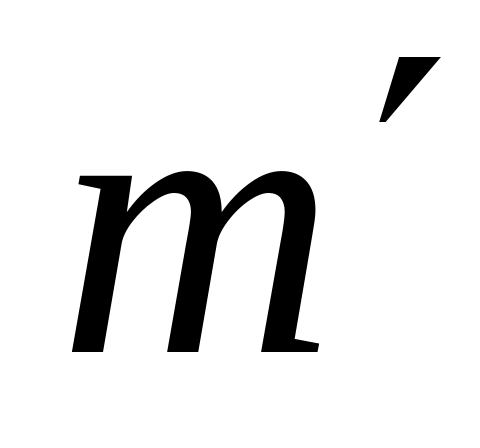=m+1 преобразуется к такому виду, как если бы оно с самого начала решения ЗЛП было представлено в симплекс-таблице, и с ним бы проводились все преобразования Гаусса-Жордана:

1. ограничение приводится к виду равенства путем введения 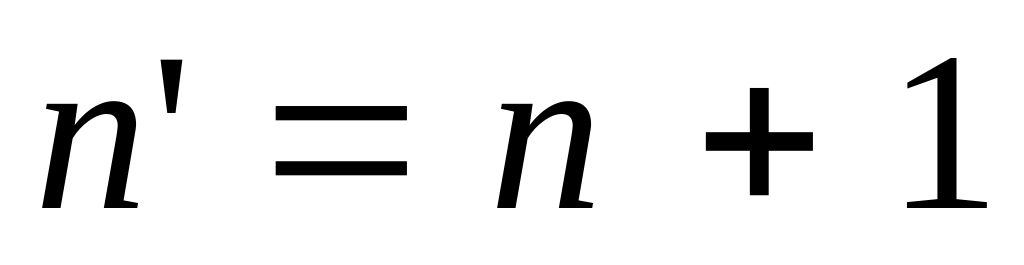балансовой переменной:

; (1.114)

б) из уравнения (1.114) исключается переменные прежней задачи, являющиеся базисными. Это делается с использованием строк матрицы и элементов вектора заключительной симплекс-таблицы :

если некоторая переменная l находится в базисе на r-ом месте , то выполняется следующая вычислительная операция

{ }´

=

Очевидно, что в результате такой операции , так как .

После удаления всех базисных переменных равенство (1.114) приводится к виду:

, (1.116)

готовому для включения в заключительную симплекс-таблицу путем ее расширения (рис.1.26 иллюстрирует процедуру преобразования симплекс-таблицы ). Если новое ограничение отсекает найденное оптимальное решение от D, то и, следовательно, выполняются условия сопряженности нового, расширенного базиса, определяемого базисным множеством .

в) начиная с , применяется двойственный симплекс-метод, результаты