Лекция № 7
1.15.2. Т-задача. Специальные алгоритмы решения.
Содержательная и формализованная постановка Т-задачи были подробно рассмотрены в 1.1.3.
,
,
,
,
,
,
.
Особенности структуры и свойства т-задачи
1) Исходные данные Т-задачи могут быть компактно представлены структурами данных, показанными на рис.1.28.
Рис.1.28
2) Закрытая Т-задача всегда
имеет допустимое и оптимальное решение.
В Т-задаче в соответствии с ее физической
сущностью исключается
исход
.
3) Любое допустимое решение Т-задачи
может быть представлено в виде матрицы
перевозок
(рис.1.29), в которой сумма
перевозок в i-ой
строке равна
,
а сумма перевозок в j-ом
столбце равна
.
Рис. 1.29
4) Если все и – целые числа, то любое допустимое базисное решение Т-задачи и, следовательно, ее оптимальное решение являются целочисленными.
5) Матрица условий A эквивалентной одноиндексной задачи линейного программирования имеет структуру, изображенную на рис. 1.30.
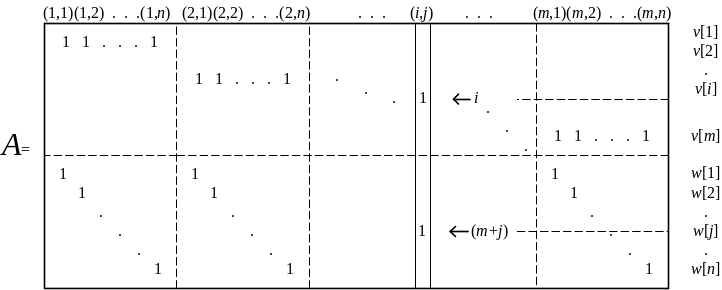
Рис. 1.30
На этом рисунке показаны только ненулевые
элементы, а также показана структура
произвольного
-го
столбца. В нем всего два не нулевых
(равных единице) элемента: один стоит в
i-ой, а второй в
-ой
строке.
6) После введения специальных обозначений для двойственных переменных Т-задачи (см. рис. 1.30):
– ставятся в соответствие первым m
ограничениям (ограничениям первого
типа),
– ставятся в соответствие n
ограничениям второго типа, -
можно следующим образом сформировать ограничения соответствующей двойственной задачи:
,
(1.153)
Для определенного базиса на основе известного свойства двойственной задачи можно следующим образом определить сиплекс-разности для каждого столбца исходной задачи:
7) Ранг матрицы условий А, а, следовательно, и размерность базиса Т-задачи определяются следующим соотношением:
. (1.154)
Из этого следует, что в Т-задаче выполнение каждого из m+n ограничений является следствием выполнения всех остальных ограничений.
8) Базисные элементы (их количество в Т-задаче равно m+n-1) никогда не образуют в матрице перевозок «цепочку», что следует из свойства линейной независимости базисных векторов
Цепочка – это система взаимосвязанных по строкам и столбцам элементов матрицы перевозок, значения которых можно сбалансировано изменять (одни – увеличивать а другие – уменьшать), не нарушая ограничений Т-задачи.
Добавления к базисным элементам любого другого элемента сразу образует в матрице перевозок цепочку, замкнутую на добавленный элемент.
Алгоритм выявления цепочки
Шаг 1. Вычеркиваются все строки матрицы перевозок, в которых осталось не более одного базисного элемента.
Шаг 2. Вычеркиваются все столбцы матрицы перевозок, в которых осталось не более одного базисного элемента.
Шаг 3. Если в пунктах 1 и 2 произошло хотя бы одно вычеркивание, то переход на 1.
Шаг 4. Если все строки и столбцы матрицы перевозок вычеркнуты, то цепочка не образовалась, иначе в не вычеркнутых строках и столбцах находятся элементы цепочки.
Указанные свойства следующим образом используются при формировании специальных алгоритмов решения Т-задачи:
– свойства 1 и 3 позволяют сформировать специальные алгоритмы решения Т-задачи, основанные на работе с более компактными (по сравнению с универсальными алгоритмами симплекс-таблиц) структурами данных;
– свойство 4 позволяет с помощью линейного программирования решать целочисленные оптимизационные задачи, в том числе, и задачу о назначении (см. 2.1.2.), родственную Т-задаче;
– свойство 6 позволяет специальным образом без использования симплекс-таблицы рассчитывать симплекс-разности;
– свойство 7 позволяет контролировать размерность базисного решения при его формировании;
– свойство 8, во-первых, позволяет формировать исходный базис из линейно-независимых столбцов матрицы A (критерий – отсутствие цепочки), а, во-вторых, - позволяет сформировать специальную процедуру корректировки базисного решения.