Лекция 13-14. Условия возрастания и убывания функций. Точки экстремума. Необходимое условие экстремума. Достаточные признаки максимума и минимума. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции. Исследование на максимум и минимум с помощью производных высшего порядка. Исследование функций на выпуклость и вогнутость точки перегиба. Асимптоты кривых. Общая схема построения графиков.

1.Пискунов Н.С. Дифференциальное и интегральное исчисление, т.1-2, М., Наука, 2000.

2.Катасонов А.М. Применение дифференциального исчисления для исследования и построения их графиков. Программированное учебное пособие. М., 1997.Тема 2-4.

3.И.П. Натансон. Краткий курс высшей математики.,М.,Лань.2005

4.Бугров Я.С., Никольский С.М.Высшая математика, Т.2,. Дифференциальное и интегральное исчисление. М., Дрофа, 2003.

гл.4.

Две следующие лекции во многом объясняют, для чего нужен тот материал, который мы пытались понять ранее. Мы переходим к теме – исследование функций.

Начнем с некоторых определений.

Определение 1. Функция называется возрастающей на отрезке если для любых двух значений из данного отрезка, таких что выполнено условие .

Функция называется убывающей на отрезке если для любых двух значений из данного отрезка, таких что выполнено условие .

Сформулируем теорему о необходимых условиях возрастания (убывания) функции.

Теорема 1. (Необходимые условия возрастания (убывания) функции на отрезке.) Если функция непрерывна на отрезке , дифференцируема на интервале и возрастает (убывает) на этом отрезке, то ее производная неотрицательна - , (неположительна - ) на этом отрезке. Доказательство проведем для первого случая. Второй рассматривается аналогично.

Так как функция дифференцируема, то существует предел . Так как этот предел существует, то он равен пределу справа . Поскольку функция возрастает на отрезке, то при имеем . По теореме о переходе к пределу в неравенствах получаем .

Далее докажем достаточные условия возрастания функции на отрезке.

Теорема 2. . (Достаточные условия возрастания (убывания) функции на отрезке.) Если функция непрерывна на отрезке , дифференцируема на интервале и ее производная положительна - (отрицательна ) на этом интервале, то данная функция возрастает (убывает) на этом отрезке. Доказательство проведем для первого случая. Второй рассматривается аналогично.

Пусть . По теореме Лагранжа , где

. Так как , то .

Важную роль при исследовании характера поведения функций играют точки экстремума.

Сформулируем некоторые определения.

Определение 2. Точка является точкой максимума (минимума) функции , если найдется , такое, что для всех значений аргумента , удовлетворяющего условию будет выполнено ( ).

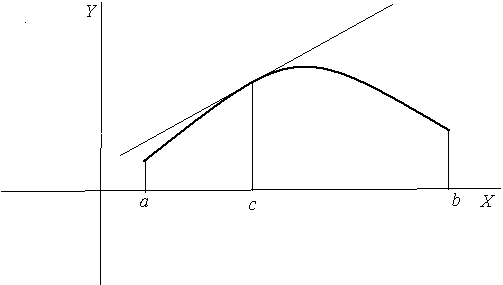
Отметим, что понятие максимума и минимума – это локальные понятия и их не надо путать с понятием наибольшее и наименьшее.

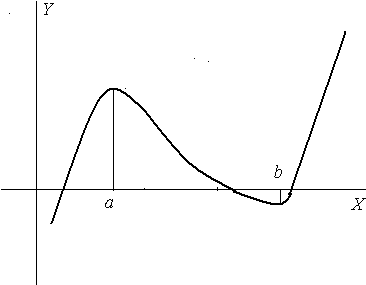
Так на приведенном рисунке точка является точкой максимума, а точка - точкой минимума. Хотя значения в этих точках не являются ни наибольшими, ни наименьшими.

Определение 3. Точки максимума и минимума называются точками экстремума функции.

Сформулируем достаточные условия экстремума.

Теорема 3. Если точка является точкой экстремума функции и эта функция имеет производную в точке , то производная в точке равна нулю .

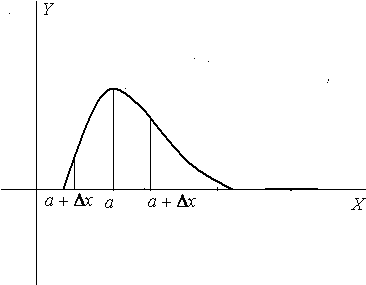
Для определенности будем считать, что - точка максимума.

Поскольку функция дифференцируема в точке , то существует предел

. Так как этот предел существует, то он равен пределам справа и слева .

При имеем , значит . По теореме о переходе к пределу в неравенствах получаем .

При имеем , значит . По теореме о переходе к пределу в неравенствах получаем .

Следовательно .

Следствие. Точками экстремума функции могут быть лишь такие точки, где производная или равна нулю или не существует.

Определение. Точки, в которых производная или равна нулю или не существует будем называть критическими точками функции.

Заметим, что условие равенства нулю производной не является достаточным условием экстремума. Простейший пример – функция . Эта функция возрастает на всей оси и точек экстремума у нее нет. Однако ее производная равна нулю при .

Далее мы займемся выводом достаточных условий экстремума функции.

Достаточные условия с помощью первой производной.

Теорема 4.(Достаточные условия экстремума с помощью первой производной). Если функция непрерывна в критической точке и при переходе через эту точку производная меняет знак с плюса на минус, то точка является точкой максимума, если производная меняет знак с минуса на плюс, то точка является точкой минимума.

Приведем доказательство первого случая, поскольку второй случай доказывается аналогично.

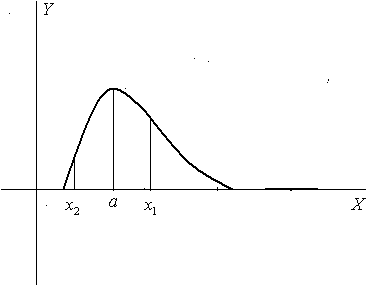
Доказательство. Дано при , при .

Пусть . Тогда по теореме Лагранжа , где . Поскольку , то .

Пусть . Тогда по теореме Лагранжа , где . Поскольку , то .

Следовательно является точкой максимума.

Достаточное условие экстремума с помощью производных высших порядков.

Теорема. Пусть функция имеет в окрестности точки непрерывные производные до порядка включительно. При этом , а . Тогда если число четное, то точка является точкой экстремума и при - точкой минимума, при - точкой максимума. Если число нечетное, то точка не является точкой экстремума.

Доказательство. Согласно формуле Тейлора имеем

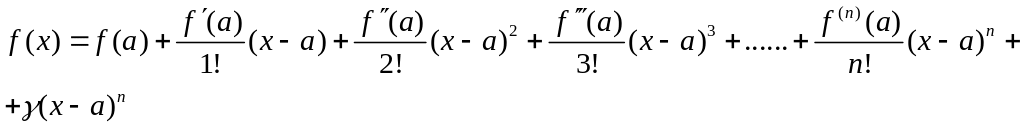
Где бесконечно-малая величина. Так как ,

то .

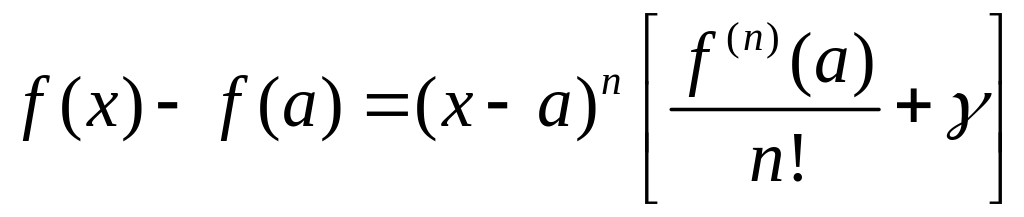Поскольку , а бесконечно-малая величина, то знак приращения функции определяется знаком выражения .

Пусть - четное число.

1. . Тогда . Значит и точка является точкой минимума.

2. . Тогда . Значит и точка является точкой максимума.

Пусть - нечетное число. Положим для определенности .

Тогда при имеем . Следовательно .

При имеем . Следовательно . Следовательно точка не является точкой экстремума.

Как правило чаще всего используется следующее следствие из данной теоремы.

Следствие. Если , а , то является точкой минимума, если , а , то является точкой максимума.

Пример. Исследовать на экстремум функцию в точке .

Имеем: ; ; ; ; ; .

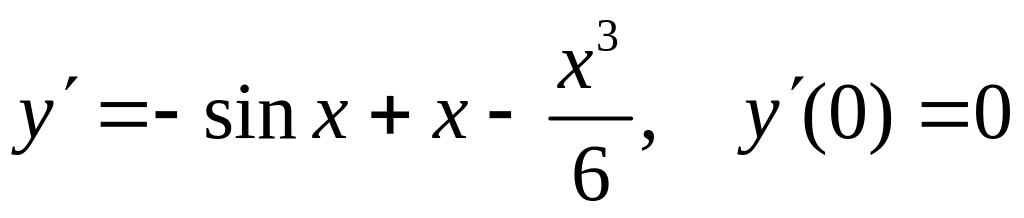Так как ненулевая производная является производной шестого порядка – четное число, то точка является точкой экстремума, а так как она отрицательна, то эта точка будет точкой максимума.

Отметим, что простейшие вопросы исследования поведения функций построения ее графика можно решать с помощью первой производной.

Пример. С помощью первой производной найти интервалы возрастания, убывания функции, точки экстремума и схематично построить ее график:

.

Исследование любой функции начинается с области допустимых значений. В данном случае областью допустимых значений является вся числовая ось.

Второй обязательный момент – это нули и точки разрыва функции.

Поскольку данная функция элементарная и она определена на всей числовой оси, то она непрерывна на всей числовой оси и точек разрыва нет.

Определим нули функции. Имеем ; ; ;

; ; . Поскольку функция может менять свой знак лишь в тех точках, где она равна нулю или в точках разрыва, то данная функция может изменить знак лишь в точках ; . Данные точки разбивают числовую ось на интервалы . Вычисляя значение функции в какой либо точке интервала составляем таблицу интервалов знакопостоянства функции

			+

Для того чтобы определить интервалы возрастания и убывания функции нам необходимо фактически определить знаки первой производной. Находим первую производную функции.

.

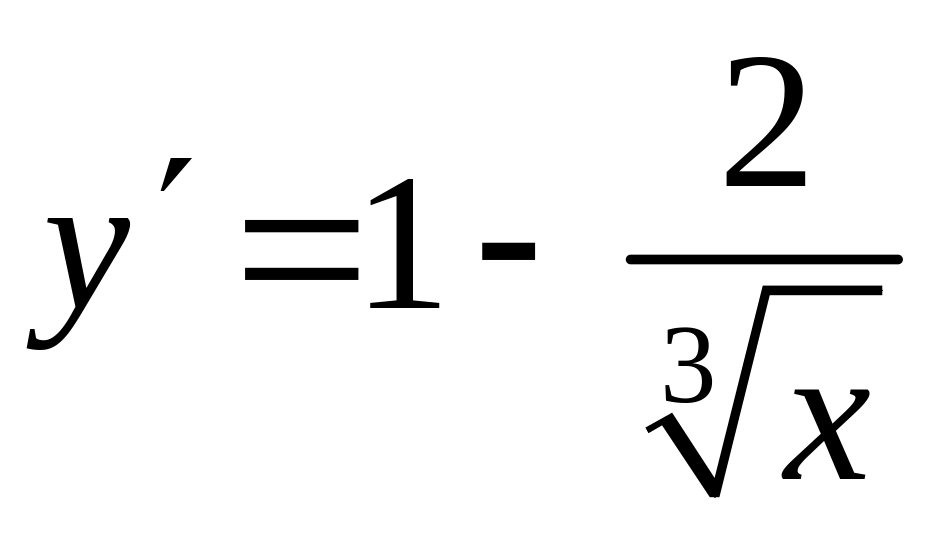Определим нули и точки разрыва первой производной.

Первая производная неопределенна при , значит эта точка является точкой разрыва. Определим нули .

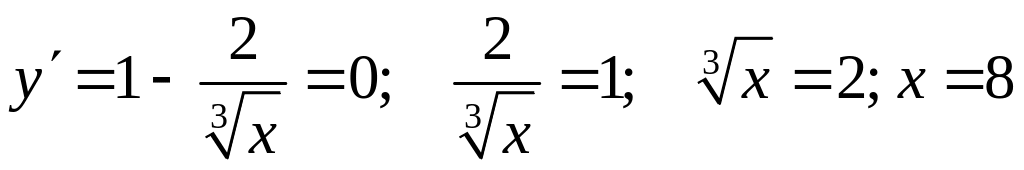Следовательно, первая производная может изменить знак при и

Определяем интервалы знакопостоянства первой производной и характер поведения функции на этих интервалах.

			+

Таким образом функция возрастает на интервалах ; , убывает на интервале .

Выясним вопрос о существовании точек экстремума. Критическими точками являются две точки ; .

Поскольку при переходе через точку производная меняет знак с(+) на (-), то точка является точкой максимума.

При переходе через точку производная меняет знак с(-) на (+), и точка является точкой минимума.

Вычислим значения функций в точках экстремума.

.

Теперь схематично построим график. Начнем с очень схематичного варианта.

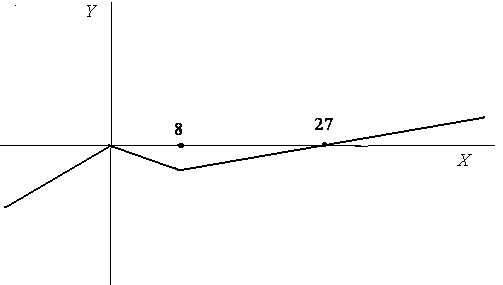
Конечно, этот график очень схематичный, но вопросы возрастания и убывания функции он отражает правильно. Но все таки, функция не состоит из прямых линий, и давайте немного сгладим график.

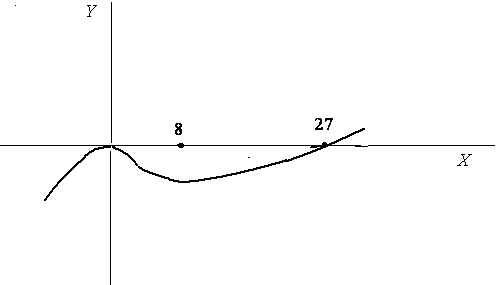
В приведенном графике есть один недостаток. Производная при значении аргумента стремящемся к стремится к бесконечности. А это означает, что касательная будет вертикальной. Поэтому более точно график выглядит так.

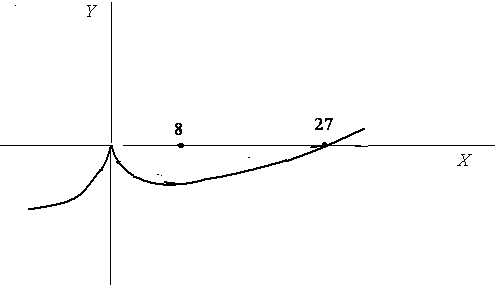
Такой максимум в точке называется колючим.

Следующая тема - отыскание наибольшего и наименьшего значений функции непрерывной на отрезке.

Мы уже знаем, что функция непрерывная на отрезке принимает на этом отрезке свое наибольшее и наименьшее значения. Давайте подумаем. Функция может принимать свое наибольшее или наименьшее значение либо внутри отрезка либо на его концах. Если эти значения достигаются внутри отрезка, то соответствующие точки являются точками экстремума функции, а значит критическими. Следовательно вопрос определения наибольшего и наименьшего значений функции на отрезке принципиально может решаться по следующей схеме.

1.Находим производную функции.

2.Определяем критические точки (в которых производная или равна нулю или не существует) и выбираем те, которые лежат на данном отрезке.

3.Вычисляем значения функции в выбранных точках и на концах отрезка. Среди вычисленных значений выбираем наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значение функции на отрезке .

Находим производную: .

Находим критические точки: ; .

На отрезке лежат , .

Вычисляем значения функции: ; ; ; .

Наибольшее значение: .

Наименьшее значение: .

Рассмотрим применение этих методов на примере некоторых практических задач.

Пример. Прямоугольный участок огорожен с трех сторон забором периметра 4p. При каких размерах сторон площадь участка S будет наибольшей.

Сначала сделаем некоторые общие замечания.

Общая схема таких задач состоит в следующем. Требуется найти наибольшее или наименьшее значение некоторой величины (назовем ее S), зависящей от двух параметров (обозначим их и ) S( , ).

При этом параметры и не являются не зависимыми, а связаны соотношением F( , )=0. Условия задачи позволяют определить возможную область изменения параметров. Это может быть отрезок или интервал.

Можно предложить следующий метод решения. Из соотношения F( , )=0 один параметр может быть выражен через другой. Например, = ( ). Тогда функция S становится функцией одного параметра S=S( , ( )). Если область возможного изменения параметра является отрезком, то дальнейшее решение в точности совпадает с решением предыдущей задачи. Если область изменения параметра является интервалом, то полезно воспользоваться следующим фактом.

Если на некотором интервале функция имеет единственную точку экстремума и эта точка является точкой максимума (минимума), то значение функции в этой точке будет наибольшим (наименьшим) на всем интервале. (Попытайтесь доказать этот факт самостоятельно.)

Теперь перейдем непосредственно к решению задачи.

Обозначим и размеры сторон прямоугольника.

Тогда S= . Параметры и не являются независимыми, а связаны соотношением (длина забора) +2 =4p. Тогда =4p2 . Следовательно, функцию S можно представить как функцию одного параметра : S= (4p2 ) .

Из условия задачи ясно, что параметр может изменяться на следующем отрезке . То есть задача сводится к отысканию наибольшего значения функции S=S( )= (4p2 ) на отрезке .

Найдем производную: . Приравнивая ее нулю, получаем =p. Найденная точка лежит на отрезке .

Вычисляем S(0)=0, S(2p)=0, - это значение и является наибольшим. Тогда размеры сторон равны: a=2p, b=p.

Пример. Объем цилиндрической цистерны равен V. При каких размерах площадь ее полной поверхности будет наименьшей.

Решение. Цилиндрическая цистерна характеризуется двумя параметрами: радиусом основания R и высотой H. Площадь полной поверхности выражается формулой S=2 +2RH. Параметры R и H не являются независимыми (известен объем), а связаны соотношением V= H. Тогда H= . Подставляя Н в выражение для площади полной поверхности, получим S как функцию одной переменной S( R )= 2 + . Возможная область изменения параметра R интервал (0;).

Найдем производную: 4R . Приравнивая ее нулю, получаем R= . Заметим что: <0 при R< , >0 при R> . Поскольку при переходе через данную критическую точку производная меняет знак с минуса на плюс, то эта точка является точкой минимума. Поскольку на интервале (0;) данная точка является единственной точкой экстремума, то значение функции в этой точке будет наименьшим. Получаем, что цистерна имеет наименьшую полную поверхность при R= , H= =2R.

Более тонкое исследование характера поведения функции и ее графика требует привлечения производных более высокого порядка. Следующая тема которой мы коснемся -исследование функций на выпуклость и вогнутость, точки перегиба.

Определение. Функция на называется выпуклой (обращена выпуклостью вверх) на интервале , если все точки кривой лежат ниже касательной, проведенной в любой точке интервала.

Функция на называется вогнутой (обращена выпуклостью вниз) на интервале , если все точки кривой лежат выше касательной, проведенной в любой точке интервала.

Докажем теорему, которая позволяет судить о направлении выпуклости графика функции.

Теорема. Если во всех точках интервала вторая производная функции отрицательна, то данная функция выпукла на этом интервале. Если во всех точках интервала вторая производная функции положительна, то данная функция вогнута на этом интервале.

Докажем для определенности первую часть теоремы. Вторая часть доказывается аналогично.

Пусть для всех . Рассмотрим произвольную точку , где . Уравнение касательной, проведенной в точке имеет вид

, а уравнение функции .

Тогда .

Рассмотрим первый случай .

По теореме Лагранжа , где , Тогда .

Согласно теореме Лагранжа , где . Следовательно . Так как , то

Второй случай .

По теореме Лагранжа , где , Тогда .

Согласно теореме Лагранжа , где . Следовательно . Так как , то и теорема доказана.

Поясним на интуитивном уровне смысл доказанной теоремы. Если вторая производная отрицательна, то первая производная убывает. А это означает, что уменьшается угол наклона касательной к оси Х. А это фактически и означает выпуклость кривой. Точно также, если вторая производная положительна, то первая производная возрастает, а значит и возрастает и угол наклона касательной к оси Х. Это и является характерным признаком вогнутой кривой.

Определение. Точка непрерывной кривой, в которой существует касательная, отделяющая выпуклую часть от вогнутой, называется точкой перегиба кривой.

Установим необходимое условие точки перегиба.

Теорема. Если некоторая точка кривой является точкой перегиба, и в этой точке существует непрерывная вторая производная, то она равна нулю в этой точке.

Доказательство. Пусть - точка перегиба. Предположим противное. Пусть для определенности . Тогда по свойству непрерывной функции вторая производная сохраняет свой знак на некотором интервале, содержащем точку . А значит на этом интервале функция вогнута. Получили противоречие.

Следствие. Точками перегиба могут являться только такие точки, в которых вторая производная или равна нулю или не существует.

Далее сформулируем достаточные условия точки перегиба.

Теорема. Пусть в точке функция непрерывна и существует касательная к графику функции в данной точке. При этом в этой точке вторая производная или равна нулю или не существует. Если при переходе через данную точку вторая производная меняет свой знак, то данная точка является точкой перегиба.

Доказательство. Положим для определенности, что при и при . Тогда при кривая выпукла, а при - вогнута. Следовательно - точка перегиба.

Теперь давайте на интуитивном уровне попытаемся разобраться в характерных особенностях точки перегиба.

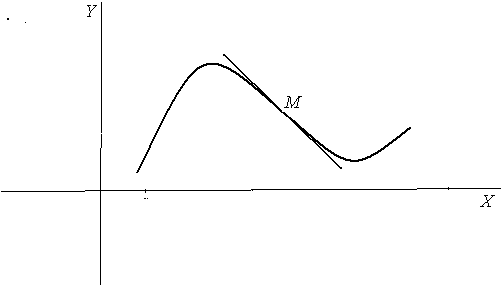
Из приведенного графика видим, что особенностью точки перегиба М является тот факт, что по разные стороны от этой точки график функции лежит по разные стороны касательной, проведенной в данной точке.

Иногда полезно примерно представлять себе характер поведения функции вдали от начала координат. Это представление дает знание асимптот. Они полезны тогда, когда при неограниченном удалении от начала координат график функции приближается к некоторой прямой.

Различают вертикальные и наклонные асимптоты.

Начнем с вертикальных асимптот.

Определение. Если или , то прямая называется вертикальной асимптотой графика функции .

Сразу заметим, что вертикальные асимптоты могут быть лишь в точках разрыва функции.

Отметим характерные особенности поведения графика функции в окрестности вертикальных асимптот. Напомню, что бесконечность бывает как со знаком плюс, так и со знаком минус.

1.

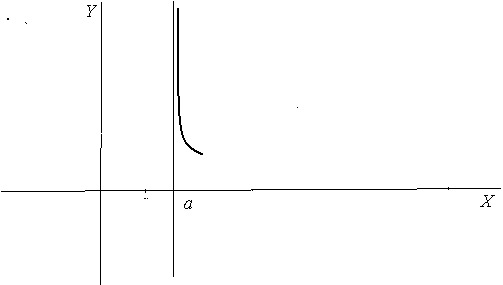
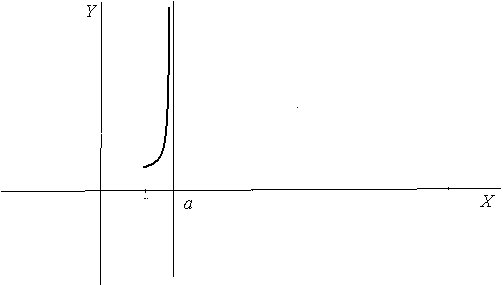
2.

3.

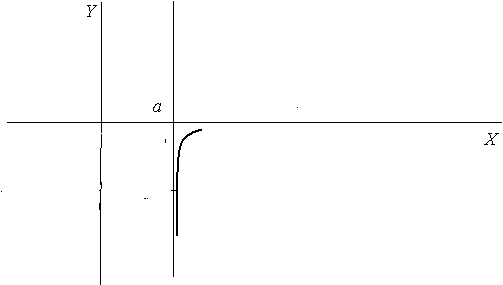
4.

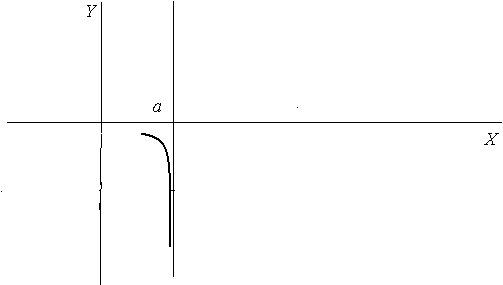
Теперь перейдем к изучению наклонных асимптот.

Определение. Прямая называется наклонной асимптотой графика функции при , если .

Аналогично определяется наклонная асимптота при .

Выведем условия существования асимптот.

Пусть . Тогда , , .

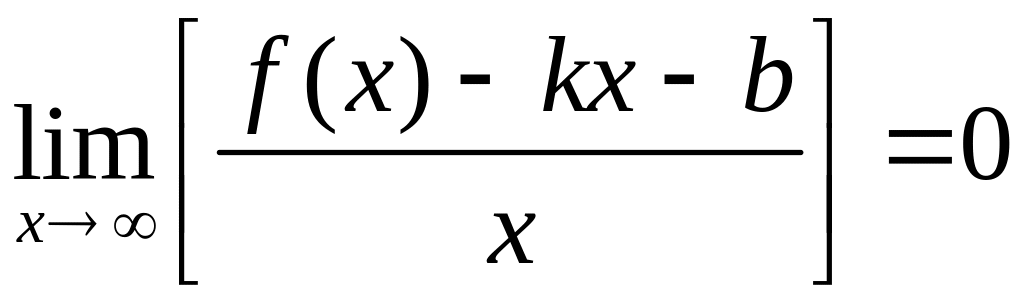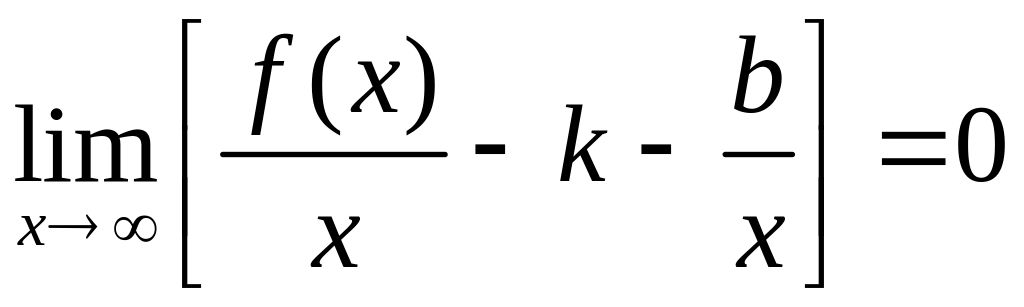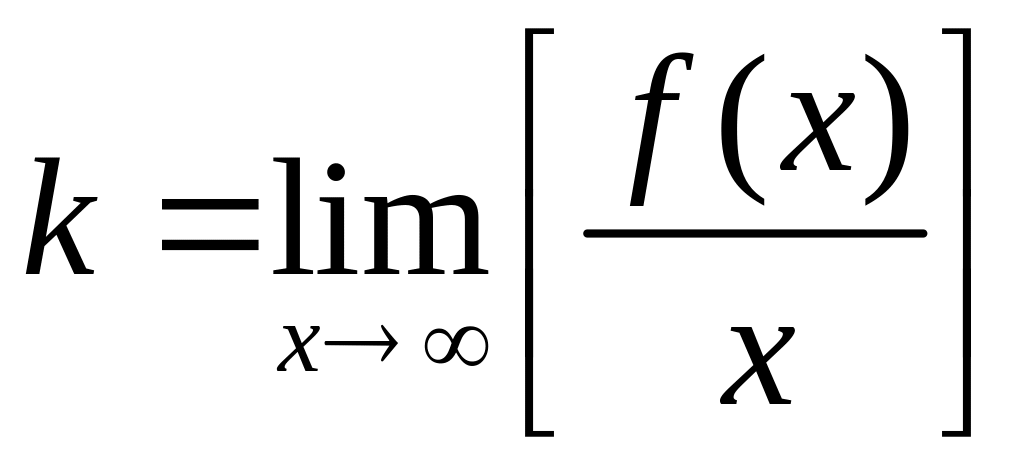То есть, если асимптота существует, то ее угловой коэффициент вычисляется по формуле

(1)

Если этот предел не существует или бесконечен, то не существует и наклонная асимптота.

Определим значение .

Имеем . То есть значение вычисляется по формуле

(2)

Если хотя бы один из пределов (1) или (2) не существует, либо бесконечен, то не существует и соответствующая наклонная асимптота.

Отметим, что непосредственно из определения наклонной асимптоты следует, что существование пределов (1) или (2) является не только необходимым, но и достаточным условием существования наклонной асимптоты.

Отметим, что знание наклонных асимптот и здравый смысл в некоторых случаях позволяют провести качественное исследование характера поведения функции.

Пример. Найти асимптоты и схематично построить график функции .

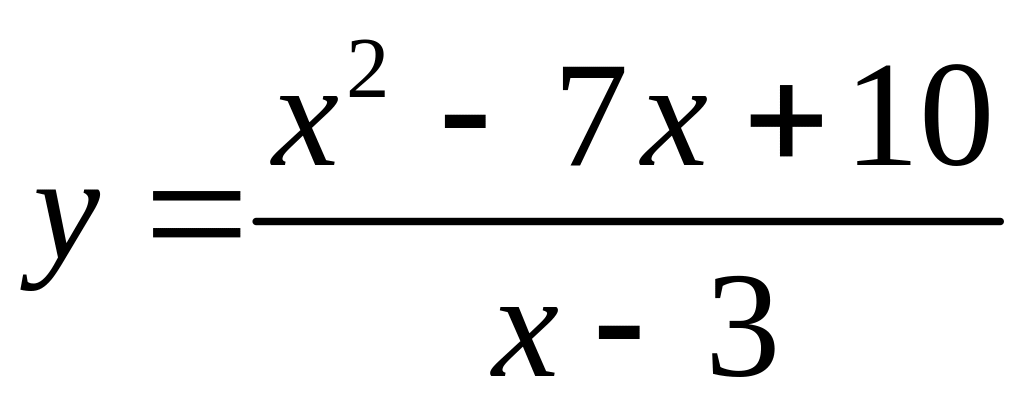Обязательным моментом любого исследования является определение ОДЗ. Данная функция определена при .

Нули и точки разрыва функции.

Нули. .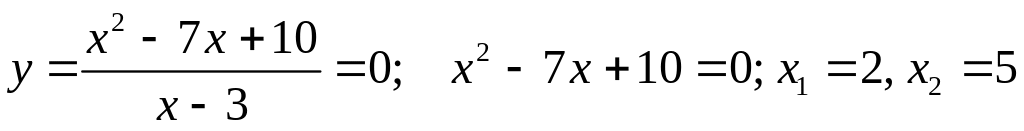

Точки разрыва .

Определяем интервалы знакопостоянства функции

		+		+

Определим вертикальные асимптоты

Вертикальная асимптота может быть лишь , как точка разрыва.

Имеем ,

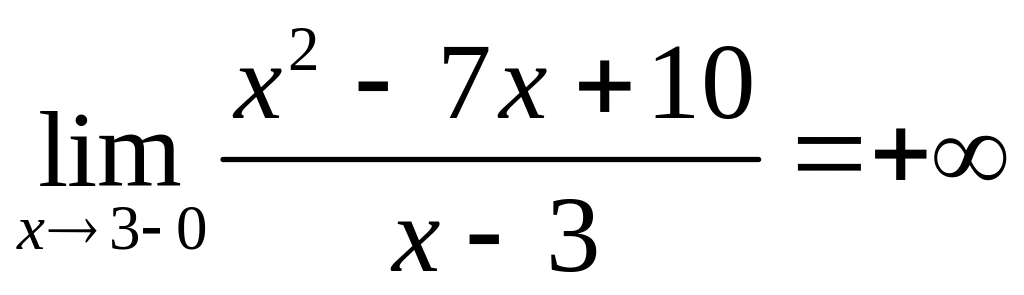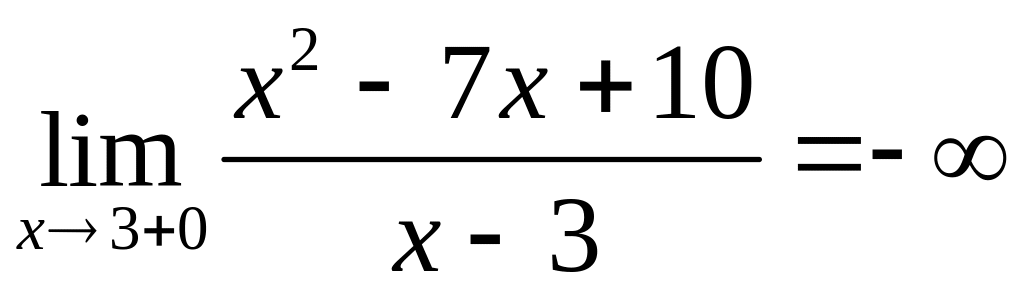
Знак бесконечности легко определяется из таблицы.

Наклонные асимптоты.

В данном примере асимптоты на плюс и минус бесконечности не отличаются, поэтому их будем вычислять одновременно.

.

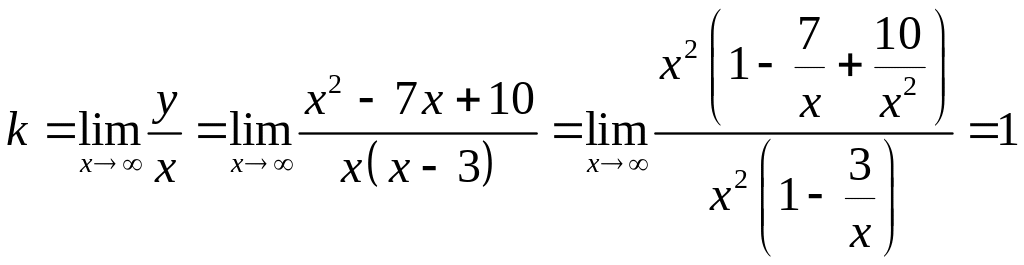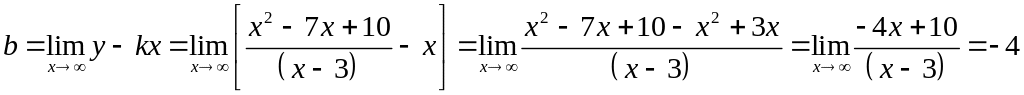
Значит уравнение наклонной асимптоты имеет вид .

Тогда используя проведенное исследование и некоторые разумные соображения можно схематично построить график.

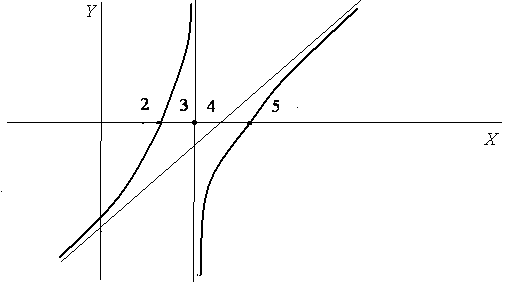
Пример. Найти асимптоты и схематично построить график функции .

Поскольку дискриминант выражения стоящего под знаком квадратного корня отрицателен, то подкоренное выражение положительно и функция определена и непрерывна на всей числовой оси. Следовательно, нет ни нулей ни точек разрыва, а значит вертикальных асимптот нет, а сама функция всегда положительна.

Найдем наклонные асимптоты. В этом примере на плюс и минус бесконечности будут разные асимптоты.

Начнем с плюс бесконечности.

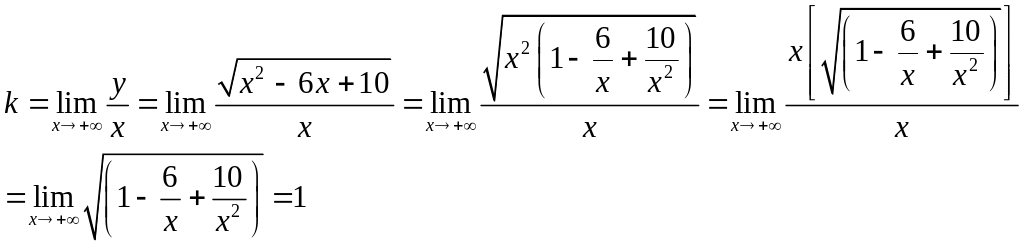
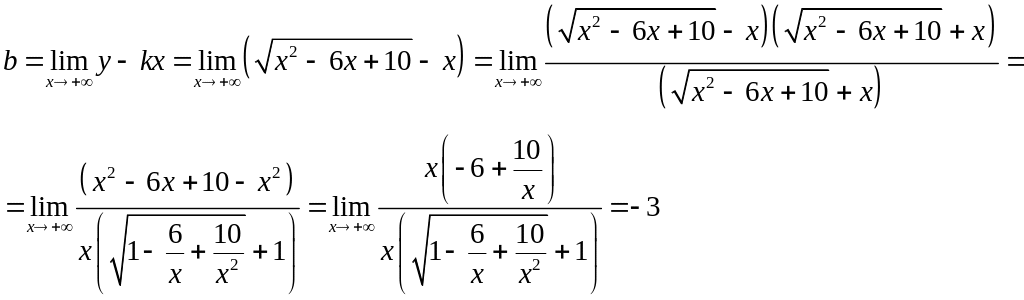
Значит уравнение наклонной асимптоты на плюс бесконечности имеет вид .

Аналогично на минус бесконечности.

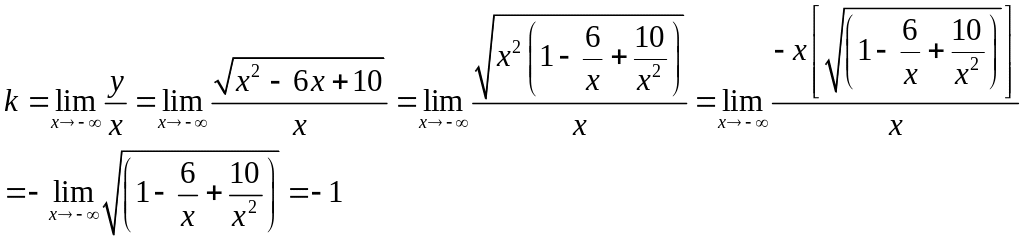
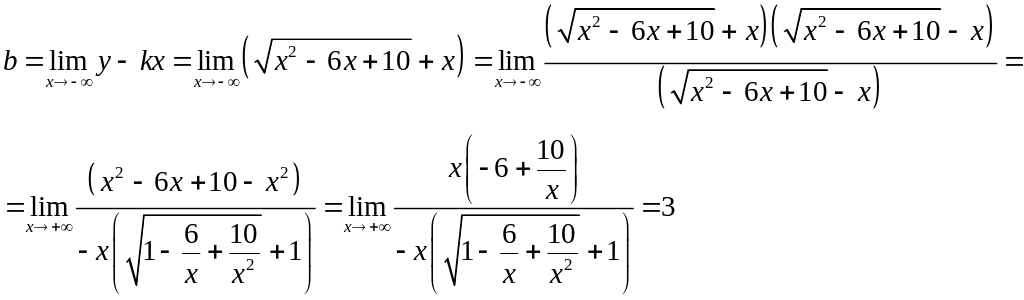Значит уравнение наклонной асимптоты на плюс бесконечности имеет вид .

Теперь мы можем позволить себе роскошь схематично построить график.

Полное исследование функции и построение ее графика.

Мы расскажем это на конкретном примере выделяя и поясняя основные существенные моменты.

Пример. Методами дифференциального исчисления провести полное исследование функции и построить ее график: .

Эту задачу мы рассмотрим более подробно. Непосредственно в ходе решения мы будем напоминать некоторые моменты теории. Схему построения графика мы покажем по шагам, предполагая, что в начале график строится на черновике, то есть схематично.

Полное исследование включает следующие моменты.

1. Область определения функции (ОДЗ).

Исследуемая функция определена на всей числовой оси за исключением тех точек, где знаменатель обращается в ноль.

Найдем эти точки: ; .

Следовательно, ОДЗ данной функции является вся числовая ось за исключением точек .

2. Четность, нечетность функции.

Напомним, что: функция называется четной, если y(-x)=y(x); функция называется нечетной, если y(-x)=-y(x). Напомним, что четная функция симметрична относительно оси Y, нечетная симметрична относительно начала координат. Если функция не является ни четной, ни нечетной, то говорят, что данная функция является функцией общего вида.

Для исследуемой функции имеем: ;

.

Следовательно, исследуемая функция является нечетной.

3. Нули, точки разрыва, точки пересечения графика с осями коор­динат.

Для определения нулей функции решаем уравнение y(x)=0.

Имеем: ; x=0. Следовательно, исследуемая функция обращается в ноль в единственной точке x=0.

Элементарная функция имеет точки разрыва только в тех точках, где она не определена. Следовательно, исследуемая функция имеет две точки разрыва , .

График функции пересекается с осью Х в тех точках, где она равна нулю. Эти точки уже найдены.

Определим точку пересечения с осью Y. Имеем y(0)=0.

Отметим, что в данной задаче точка пересечения с осью Х и точка пересечения с осью Y совпали, то есть график функции проходит через начало координат.

4. Интервалы знакопостоянства функции.

Для определения интервалов знакопостоянства функции напомним следующий факт.

Функция может изменить свой знак лишь при переходе через такие точки, в которых она равна нулю или имеет точку разрыва.

Исследуемая функция равна нулю при х=0. Имеет точки разрыва при х=-1 и х=1. Эти точки разбивают числовую ось на интервалы: (;1); (1;0); (0;1); (1; ). На каждом из интервалов функция сохраняет постоянный знак. Чтобы определить знак функции на любом интервале, достаточно ее вычислить в любой точке интервала. Например, определим знак на интервале (0;1). Возьмем точку , лежащую на этом интервале. Вычислим 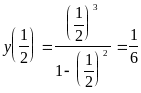>0. Следовательно, исследуемая функция положительна на интервале (0;1). Аналогично исследуются знаки функции на остальных интервалах. Результаты удобно свести в таблицу.

x (интервал изменения)	(;1)	(1;0)	(0;1)	(1; )
у (знак функции)				

5. Асимптоты графика функции.

5а. Вертикальные асимптоты.

Напомним, что прямая х=а является вертикальной асимптотой графика функции у=у(х), если хотя бы один из пределов или равен бесконечности. Вертикальные асимптоты могут быть только в точках разрыва функции.

В исследуемой функции имеются две точки разрыва. При стремлении к этим точкам знаменатель дроби стремится к нулю, а числитель к ненулевой конечной величине. Следовательно, выражение будет стремиться к бесконечности. Знак бесконечности можно определить из таблицы интервалов знакопостоянства функции. Например, в окрестности точки х=-1 (x<-1) функция положительна. Следовательно

= .

Аналогично:

= ;

= ;

= .

5Б. Наклонные асимптоты.

Напомним, что прямая y=kx+b является наклонной асимптотой графика функции y=y(x) при x+, если .

Достаточные условия существования асимптот и формулы для нахождения параметров k и b имеют вид.

; .

Если хотя бы один из этих пределов не существует или равен бесконечности, то функция не имеет асимптот при x+. Аналогично определяется асимптота при x.

В исследуемой задаче асимптоты при x и при x + одинаковы. Поэтому мы будем рассматривать предел при x .

.

.

Уравнение наклонной асимптоты имеет вид y=-x.

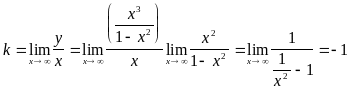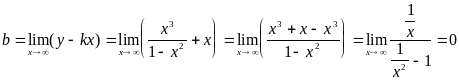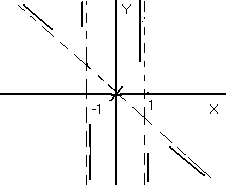
С этого момента на черновике можно начинать строить схему графика. Нанесем точки пере­сечения с осями координат, асимптоты и поведение функций около асимптот.

6. Интервалы возрастания, убывания функции. Точки экстремума.

Напомним достаточные условия возрастания (убывания) на отрезке.

Если производная функции положительна (отрицательна) во всех точках отрезка, то функция возрастает (убывает) на этом отрезке.

Необходимые и достаточные условия экстремума были сформулированы ранее.

6а. Найдем производную функции.

.

6б. Определим интервалы знакопостоянства производной. Интервалы возрастания и убывания функции.

Интервалы знакопостоянства производной определяются по той же схеме, что и ранее определялись интервалы знакопостоянства функции.

Производная имеет точки разрыва при х=-1, х=1.

Производная равна нулю: ; ; х=0, , x= .

Точки х=-1, х=1, х=0, , разбивают числовую ось на 6 интервалов. Как и ранее определяем знак производной на каждом интервале. На основании знака производной делаем вывод о характере поведения функции на интервале (возрастание или убывание). Результаты удобно свести в таблицу. В таблице

з нак указывает на возрастание функции, знак на убывание.

x			(-1;0)	(0;1)	(1; )	( ;)
y		+	+	+	+	
y