Лекция № 3

1.2. Графическая интерпретация злп и связанные с этим понятия линейного программирования

Графически ЗЛП может быть представлена и решена лишь для случая двух оптимизационных переменных. Несмотря на такую малую размерность, рассмотрение графического изображения позволяет выявить многие характерные свойства ЗЛП произвольной размерности, связанные с ней понятия и определить стратегию работы алгоритма поиска её оптимального решения.

Рассмотрим задачу

, (1.14)

,

.

Использование здесь для обозначения типа ограничения условий , и говорит о том, что каждое конкретное (i-ое) ограничение может быть одного из этих типов. Приведенные здесь условия неотрицательности оптимизационных переменных являются в общем случае необязательными.

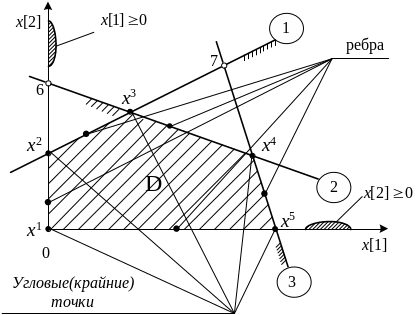
Графическое отображение D

Графическое отображение отдельного ограничения – прямой линией, для неравенств – со штриховкой наложенной в сторону полуплоскости, где неравенство выполняется.

D - выпуклый многогранник, ограниченный отрезками прямых. Несложно себе представить, что в задаче с тремя переменными допустимое множество в общем случае будет не плоским, а объемным выпуклым многогранным множеством, ограниченным плоскостями. Строго показано, что в n-мерном случае множество D также представляет собой выпуклое многогранное множество, ограниченное гиперплоскостями.

Гиперплоскостью в n-мерном Евклидовом пространстве называется множество

. (1.15)

Угловой (крайней) точкой не пустого выпуклого многогранного множества в n-мерном Евклидовом пространстве называется такая его точка, которая образована пересечением гиперплоскостей, ограничивающих D.

Ребром не пустого выпуклого многогранного множества D в n-мерном Евклидовом пространстве называется такое его подмножество, которое образовано пересечением

(n-1)-ой гиперплоскостей, ограничивающих D. Геометрически – это всегда отрезки прямых линий, соединяющих соседние угловые точки.

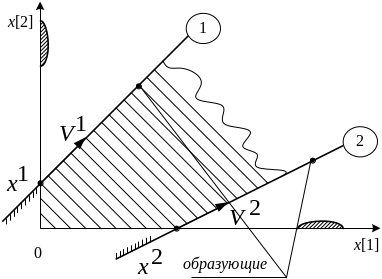
Образующей не пустого выпуклого многогранного множества D в n-мерном Евклидовом пространстве называется такое его ребро, которое имеет бесконечно удаленную точку. Уравнение образующей записывается в векторной форме следующим образом:

, (1.17)

где - угловая точка, являющаяся началом образующей;

- направляющий вектор образующей;

- скалярная величина, большая нуля, определяющая положение точки х.

Рис. 1.4	Рис. 1.5	Рис. 1.6
Рис. 1.7	Рис. 1.8	Рис. 1.9

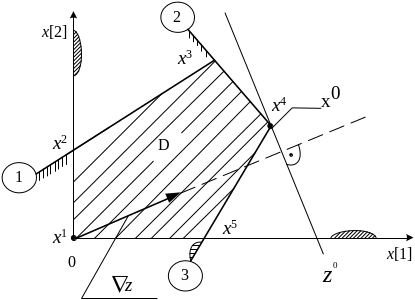
1.2.2. Графическое представление целевой функции злп

Градиент целевой функции ЗЛП:

… , … , (1.18)

Линия уровня целевой функции ЗЛП (сечение линейной целевой функции на уровне ):

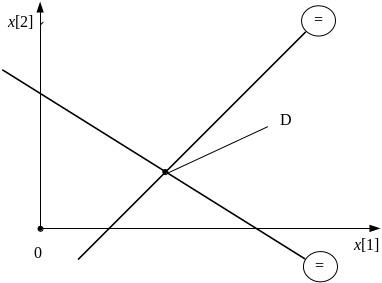
1.2.3. Графическое решение злп

1.3. Формы записи злп

Общая форма записи ЗЛП имеет следующий вид:

- направление оптимизации max или min

(или ) , (1.19)

- ограничения любых видов

или или = , , (1.20)

- не на все оптимизационные переменные накладывается условие неотрицательности, т.е. часть из них могут быть свободными

, , где (1.21)

Стандартная форма записи ЗЛП

Характеризуется тем, что все ограничения ЗЛП записаны в виде неравенств типа " " и свободные оптимизационные переменные отсутствуют:

, , (1.22)

, . (1.23)

Особо необходимо отметить случай, когда при записи ЗЛП в стандартной форме все правые части ограничений являются неотрицательными величинами ( , ), например, в производственной задаче. В этом случае, как будет показано ниже, можно сразу начинать поиск оптимального решения, минуя этап поиска допустимого решения.

Каноническая форма записи ЗЛП

Характеризуется следующими свойствами:

- направление оптимизации – max

, (1.24)

- все ограничения – типа "="

, , (1.25)

- все оптимизационные переменные – несвободные (в этом случае говорят, что имеет место однородные условия неотрицательности оптимизационных переменных)

, . (1.26)

Каноническая форма является наиболее важной среди других форм записи ЗЛП, т.к. формальные алгоритмы решения работают с ЗЛП, приведенной к этой форме.

Рассмотрим способы приведения ЗЛП к канонической форме записи:

1. Изменение направления оптимизации с min на max осуществляется умножением целевой функции на "-1":

. (1.27)

В ЗЛП этот переход соответствует изменению знаков коэффициентов целевой функции с[j] на противоположные.

2. Переход от ограничения типа " " к ограничению типа "=" осуществляется путем введения дополнительной (балансовой) оптимизационной переменной.

Пусть в исходной задаче ЗЛП с n оптимизационными переменными среди всех ограничений имеется единственное ограничение типа " "

. (1.28)

Вводится новая (так называемая дополнительная, или балансовая) переменная

, (1.29)

на которую накладывается условие неотрицательности

. (1.30)

Балансовой эта переменная называется потому, что она характеризует расхождение (дисбаланс) между левой и правой частями исходного ограничения типа "неравенство".

Очевидно, что соотношение (1.29), переписанное в виде

, (1.31)

и условие неотрицательности (1.30), добавляемое к (1.31), можно рассматривать как ограничения преобразованной задачи, эквивалентно заменяющие исходное ограничение (1.28).

Теперь рассмотрим случай преобразования ограничения типа " ":

. (1.32)

В предположении, что (1.32) – это единственное имеющиеся в исходной задаче ограничение типа неравенства, введем балансовую переменную

(1.33)

с условием ее неотрицательности

. (1.34)

Тогда равенство (1.33), переписанное в виде

(1.35)

вместе с условием (1.34) можно рассматривать как ограничения преобразованной задачи, эквивалентно заменяющие исходное ограничение (1.32).

Таким образом, можно сформулировать следующие правило перехода от ограничений типа неравенства к ограничениям типа равенства:

Переход осуществляется путем введения в левую часть ограничений дополнительных (балансовых) переменных, удовлетворяющих условиям неотрицательности, причем, - со знаком "+" для неравенства типа " " и со знаком "-" для неравенств типа " ".

Необходимо отметить, что если ограничений типа "неравенство" в исходной задаче несколько (например, l), то при переходе к равенствам должно быть введено такое же число балансовых переменных с соответствующими номерами: n+1, n+2, … , n+l.

3. Переход к однородным условиям неотрицательности оптимизационных переменных осуществляется также за счет введения новых переменных.

Предположим, что в исходной задаче имеется единственная свободная переменная x[j] и к моменту осуществления данного преобразования в ЗЛП имеется n оптимизационных переменных. Делается следующая замена переменных:

(1.36)

где и .

Такая замена основана на том очевидном факте, что любое значение переменной x[j] (и положительное, и отрицательное) может быть определено, как разность значений двух новых неотрицательных переменных. Одна из новых переменных x'[j] формально занимает место старой переменной x[j], а номер второй переменной определяется с учетом числа переменных исходной задачи и увеличения этого числа за счет сделанных до этого других преобразований. После нахождения оптимального решения ЗЛП значение исходной переменной x[j] определяется в соответствии с (1.36)

4)Переход от многоиндексной к одноиндексной задаче осуществляется путем сквозной перенумерации многоиндексных оптимизационных переменных и соответствующих им параметров задачи. Так на примере Т-задачи эта перенумерация делается путем присвоения каждой паре сквозного номера:

{(1,1), … , (1,n), (2,1), … , (2,n), … , (m,1) , … , (m,n)} ~

{ 1 , … , n , n+1 , … , 2n , … ,n (m-1)+1, … , m n}.