Механічні коливання та хвилі

4.Коливання

У цьому розділі фізики розглядаються коливання та процеси їх поширення (хвилі) у різних середовищах: рідині, атмосфері, корі земної поверхні, поверхні океанів, електромагнітні коливання у вакуумі та багато інших. Головна мета розділу - познайомити студента з основними ідеями, загальними для усіх коливань, що дозволяють побудувати їх фізичні і математичні моделі - канонічні диференціальні рівняння коливань та хвилі. Указані моделі, як універсальні, можна застосувати до окремих явищ, таких як сейсмічні коливання, виникнення та поширення цунамі, радіохвиль та ін.

У межах програми вищої математики наведені приклади розв'язку канонічних рівнянь вільних та вимушених коливань, виведення рівняння хвилі.

4.1. Коливальний рух

Коливальним рухом називається рух, що повторюється в часі. Якщо повторюваність відбувається за один і той же проміжок часу Т, то рух називається періодичним, а час Т  періодом. За період здійснюється одне повне коливання. Частота коливань  число повних коливань за одиницю часу. Рівняння коливання описує залежність зміщення тіла х з положення рівноваги від часу t.

Гармонічним називається коливання, рівняння якого описується функцією синуса або косинуса від часу  кінематичне визначення, наприклад,

х = А·cos(t + ). (1)

В цьому виразі х  зміщення від положення рівноваги, А  амплітуда коливань (максимальне зміщення),  - циклічна частота, Ф(t)=t+  фаза коливань, Ф(t=0) =   початкова фаза. Знайдемо період гармонічних коливань T, знаючи, що період косинуса є 2. Запишемо функцію косинуса в (1), ввівши період Т

. (2)

З (2) вилучимо доданок Т і прирівняємо його до періоду косинуса

. (3)

Таким чином ми одержали звязок періода T й частоти  через циклічну частоту .

Я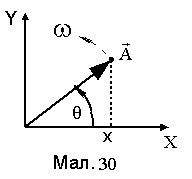 кщо рух тіла спричиняється пружною силою, або квазипружною силою (величина сили пропорційна зміщенню тіла зі стану рівноваги)  то такі коливання будуть також гармонічними. Це є динамічне визначення гармонічних коливань.

Гармонічне коливання можна представити графічно за допомогою вектора , який обертається в площині ХОУ з частотою  (див. Мал. 30). Модуль вектора дорівнює амплітуді коливання, а кут , який він складає з віссю ОХ, дорівнює фазі коливання, тобто =Ф=t+. Величина проекції х вектора А на вісь ОХ здійснює коливання по гармонічному закону х=А·cos(t+). Графічне зображення гармонічного коливання називається методом векторних діаграм.

В комплексній формі гармонічне коливання можна представити у вигляді:

,

де Z₀ = A·e^i  комплексна амплітуда, модуль якої дорівнює Z₀=A, а =argZ₀  аргумент. Фізичний зміст має дійсна частина комплексної величини Z, а саме , або уявна частина , які представляють гармонічні коливання величин х та y відповідно.

4.2. Пружинний маятник

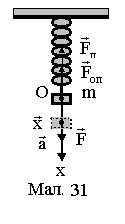Пружинний маятник являє собою тіло, підвішене на пружині, масою якої, порівнюючи з масою тіла m, можна знехтувати (див.Мал.31). Створимо зовнішньою силою зміщення маятника зі стану рівноваги . Напрямок сили буде співпадати з напрямком прискорення маятника . У протилежному напрямку будуть діяти пружна сила та сила опору . Величина пружної сили F_п = kx, де х  величина зміщення тіла зі стану рівноваги, k  жорсткість пружини, а сила опору дорівнює , де коефіцієнт опору. Лінійна залежність пружної сили від зміщення виконується лише для малих амплітуд коливань, коли виконується закон Гука.

Рівняння другого закону Ньютона для тіла тепер має вигляд

. (1)

Усі сили , що діють на тіло й вектор прискорення , лежать на одній прямій, а тому, взявши напрямок прискорення за додатній, запишемо рівняння (1) в алгебраїчній формі

. (2)

Підставимо в (2) значення сил і запишемо його у канонічній формі

, (3)

де , , ₀  власна частота, яку називають частотою вільних незгасаючих коливань,  коефіцієнт згасання коливань. Період вільних незгасаючих коливань

.