2. Факторний експеримент другого порядку

Плани другого порядку використовують для опису області оптимуму поліномами другого порядку вигляду:

.

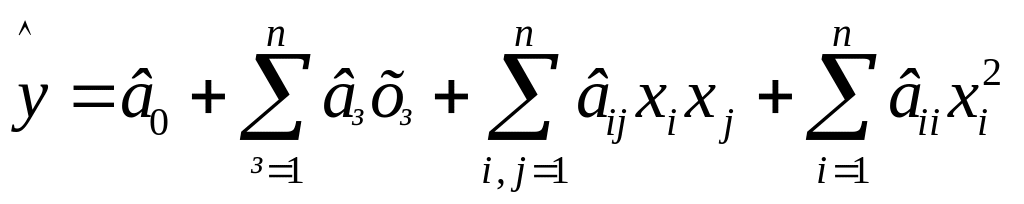Для отримання такої моделі можна використати плани на трьох рівнях 3ⁿ. Але при кількості факторів n > 4 вони стають неекономічними внаслідок великої кількості дослідів. Наприклад, реалізація такого плану для n = 5 потребує виконання N = 3⁵ = 243 дослідів.

Боксом і Уілсоном було запропоновано доповнювати дворівневий план ПФЕ “зоряними” точками. Загальна кількість дослідів за такими планами складає:

N = 2ⁿ + 2n + N₀,

де 2ⁿ – кількість дослідів за ПФЕ першого порядку;

2n – кількість “зоряних” точок;

N₀ – кількість “нульових” точок в центрі плану.

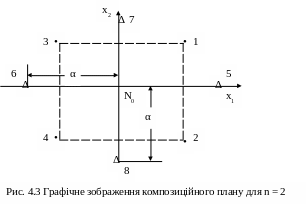
Вони є більш економічними, ніж плани 3ⁿ. Наприклад, вже при n = 4 в плані 3ⁿ кількість дослідів складає N = 3⁴ = 81, у той час, як при реалізації запропонованих планів N = 2⁴ + 2*4 + 1 = 25 (при N₀ = 1). Вибір плеча “зоряних” точок і числа “нульових” точок залежить від вибраного критерію оптимальності плану. Принцип побудови таких планів на прикладі n = 2

пояснює рис. 4.3 і табл. 4.14.

Точки 1, 2, 3, 4 утворюють ПФЕ 2ⁿ; точки 5, 6, 7, 8 - “зоряні” точки з координатами (±α; 0) та (0; ±α) ; в центрі плану знаходиться точка нульового рівня з координатами (0; 0).

Найбільш широкого застосування набули ортогональні та рототабельні плани другого порядку.

В ортогональних планах приймають кількість дослідів в центрі плану N₀ =1; величину плеча “зоряних” точок знаходять з відповідних таблиць. Наприклад, для n = 2; α = 1,0; для n = 3; α = 1,215; для n = 4; α = 1,414. Окрім того, в план вводять додаткові кодовані змінні:

.

Матриця такого плану для n = 3 наведена в табл. 4.15

Таблиця 4.14

Матриця композиційного плану другого порядку для n = 2

№№ дослідів	х0	х1	х2	Змінна стану у
1	+1	+1	+1	у1
2	+1	-1	+1	у2
3	+1	+1	-1	у3
4	+1	-1	-1	у4
5	+1	+α	0	у5
6	+1	-α	0	у6
7	+1	0	+α	у7
8	+1	0	-α	у8
9	+1	0	0	у9

Таблиця 4.15

Матриця ортогонального композиційного плану для n = 3

№№	х0	План						х1х2	х1х3	х2х3	У
		х1	х2	х3	х1/	х2/	х3/
1	+1	+1	+1	+1	+0,27	+0,27	+0,27	+1	+1	+1	у1
2	+1	-1	+1	+1	+0,27	+0,27	+0,27	-1	-1	+1	у2
3	+1	+1	-1	+1	+0,27	+0,27	+0,27	-1	+1	-1	у3
4	+1	-1	-1	+1	+0,27	+0,27	+0,27	+1	-1	-1	у4
5	+1	+1	+1	-1	+0,27	+0,27	+0,27	+1	-1	-1	у5
6	+1	-1	+1	-1	+0,27	+0,27	+0,27	-1	+1	-1	у6
7	+1	+1	-1	-1	+0,27	+0,27	+0,27	-1	-1	+1	у7
8	+1	-1	-1	-1	+0,27	+0,27	+0,27	+1	+1	+1	у8
9	+1	1,215	0	0	0,746	-0,73	-0,73	0	0	0	у9
10	+1	-1,215	0	0	0,746	-0,73	-0,73	0	0	0	у10
11	+1	0	1,215	0	-0,73	0,746	-0,73	0	0	0	у11
12	+1	0	-1,215	0	-0,73	0,746	-0,73	0	0	0	у12
13	+1	0	0	1,215	-0,73	-0,73	0,746	0	0	0	у13
14	+1	0	0	-1,215	-0,73	-0,73	0,746	0	0	0	у14
15	+1	0	0	0	-0,73	-0,73	-0,73	0	0	0	у15

Наприклад, значення х₁^/ в дослідах 1 ÷ 8 визначаються наступним чином:

- в дослідах 9,10:

;

- в дослідах 11 ÷ 15:

.

Коефіцієнти регресії обчислюють за формулами:

в₀^/ = ; ; ; ; ,

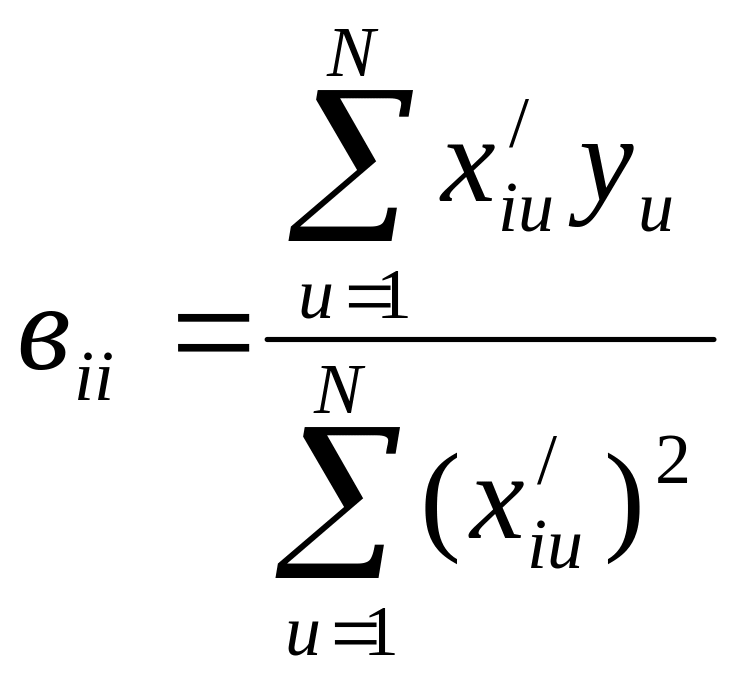де .

Дисперсії коефіцієнтів визначають за формулами:

; ; ; ,

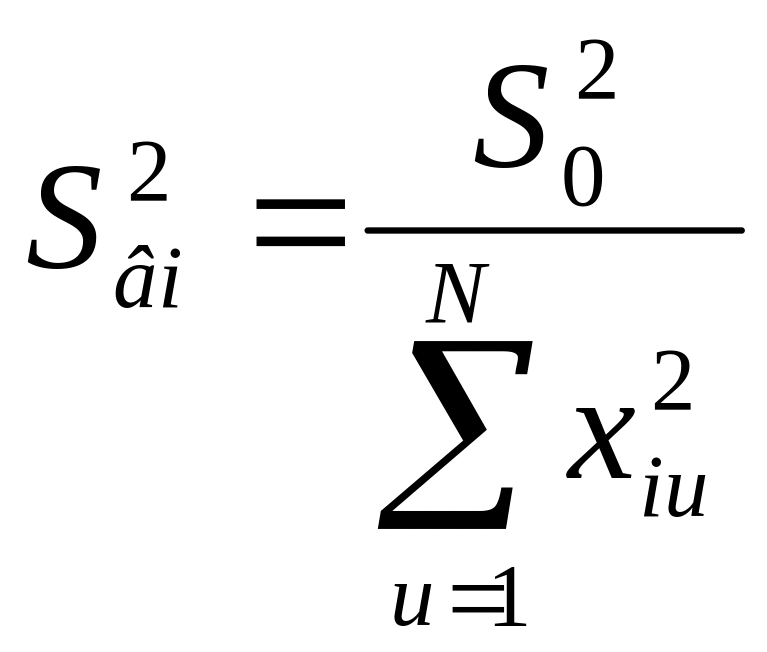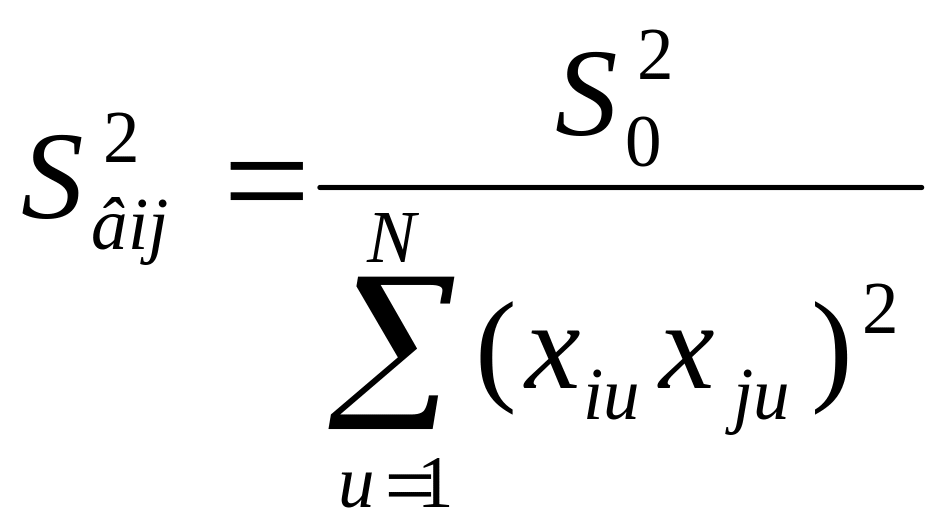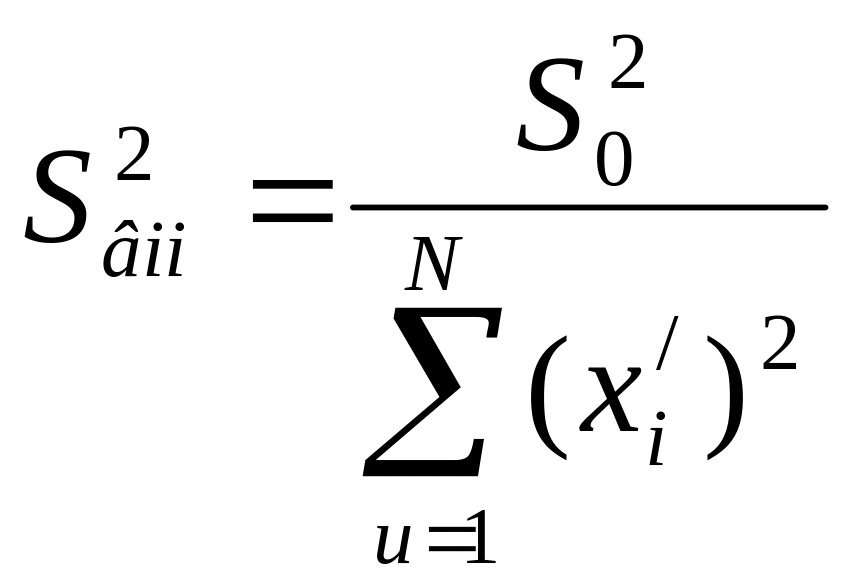де S₀² – помилка досліду.

Оцінка значимості коефіцієнтів виконується за критерієм Стьюдента, як і для планів ПФЕ.

Дисперсію адекватності знаходять за формулою:

,

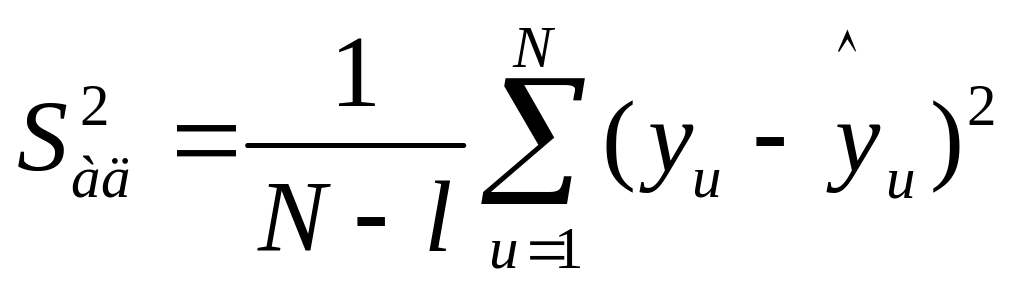де l – число членів рівняння регресії, які залишилися після відсіювання незначущих коефіцієнтів.

Адекватність також перевіряють, як і для планів ПФЕ, за критерієм Фішера.

Рототабельні плани були запропоновані Боксом та Хантером. “Зоряні” точки в них будують на відстані від центру плану α = ; рекомендована кількість дослідів в центрі плану (нульових точок) наведена в табл. 4.16, приклад рототабельного композиційного плану для n = 2 факторів – в табл. 4.17.

Розрахунок коефіцієнтів регресії виконується за формулами:

,

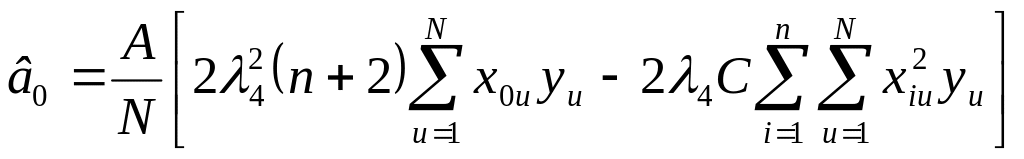де допоміжні параметри визначають за виразами:

; ;

; ; .

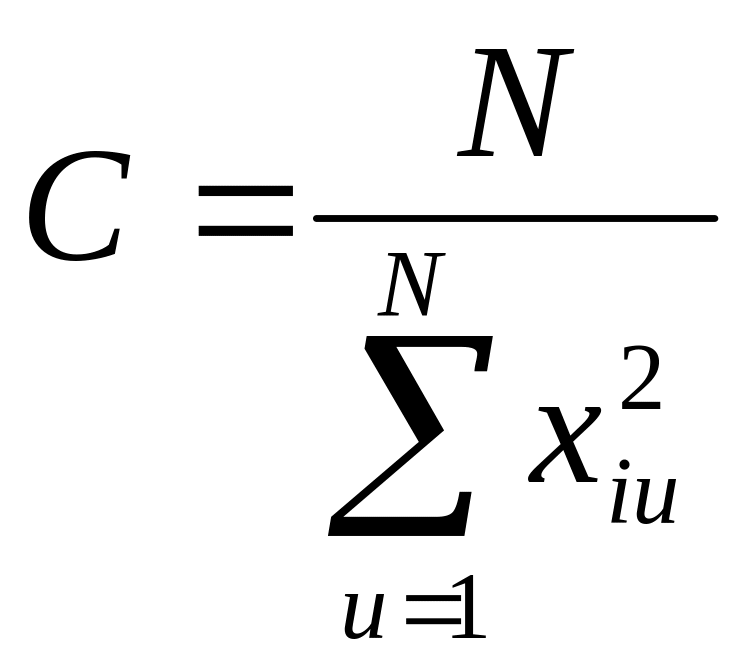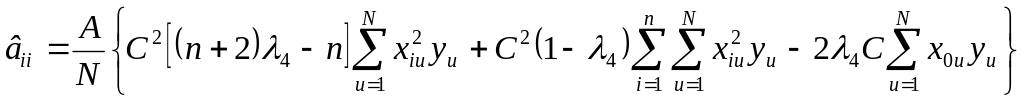Таблиця 4.16

Параметри рототабельних планів

Параметр	План
	n = 2	n = 3	n = 4	n = 5
Число «зоряних» точок	4	6	8	10
Число дослідів ядра плану	4	8	16	32
Число нульових точок	5	6	7	10
«Зоряне» плечо	1,414	1,682	2,000	2,378

Таблиця 4.17

Матриця двохфакторного рототабельного композиційного плану другого порядку

№№ дослідів	х0	План					уu
		Х1	х2	х12	х22	х1х2
1	+1	+1	+1	+1	+1	+1	у1
2	+1	-1	+1	+1	+1	-1	у2
3	+1	+1	-1	+1	+1	-1	у3
4	+1	-1	-1	+1	+1	+1	у4
5	+1	1,141	0	2,0	0	0	у5
6	+1	-1,141	0	2,0	0	0	у6
7	+1	0	1,141	0	2,0	0	у7
8	+1	0	-1,141	0	2,0	0	у8
9	+1	0	0	0	0	0	у9
10	+1	0	0	0	0	0	у10
11	+1	0	0	0	0	0	у11
12	+1	0	0	0	0	0	у12
13	+1	0	0	0	0	0	у13

Помилку досліду, тобто, дисперсію репродукційності, визначають за результатами дослідів в центрі плану:

.

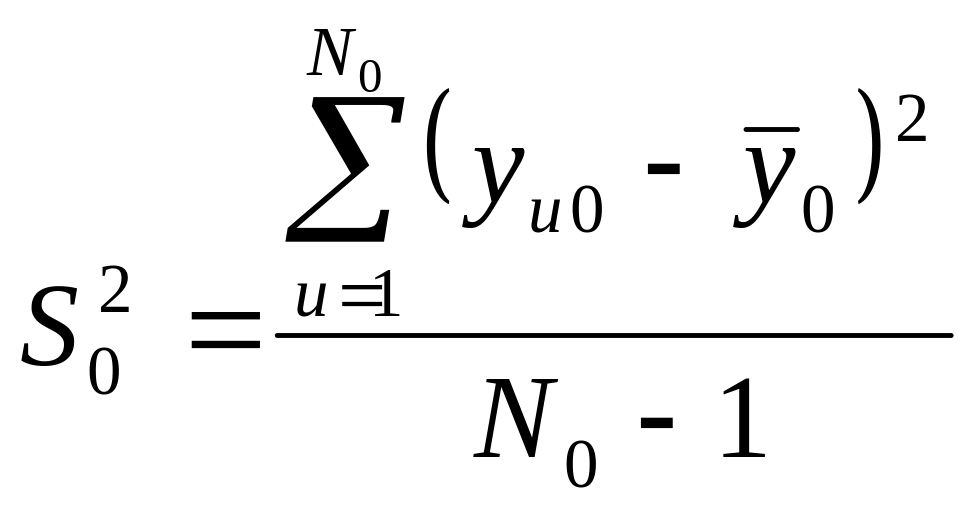Дисперсії коефіцієнтів обчислюють за формулами:

; ; ; .

Перевірка значимості коефіцієнтів проводиться за критерієм Стьюдента:

; ; ;

для числа ступенів свободи f₀ = N₀ – 1 і рівня значимості q.

Для перевірки адекватності моделі розраховують суму квадратів відхилень експериментальних даних у_u від прогнозованих :

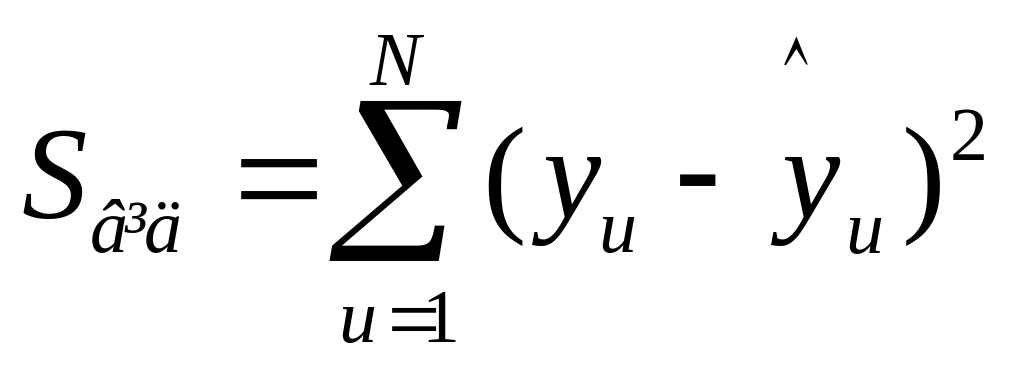
і число ступенів свободи:

f_від = N – l,

де l – кількість членів в рівнянні регресії, які залишилися після відсіювання незначущих коефіцієнтів.

Потім визначають критерій Фішера:

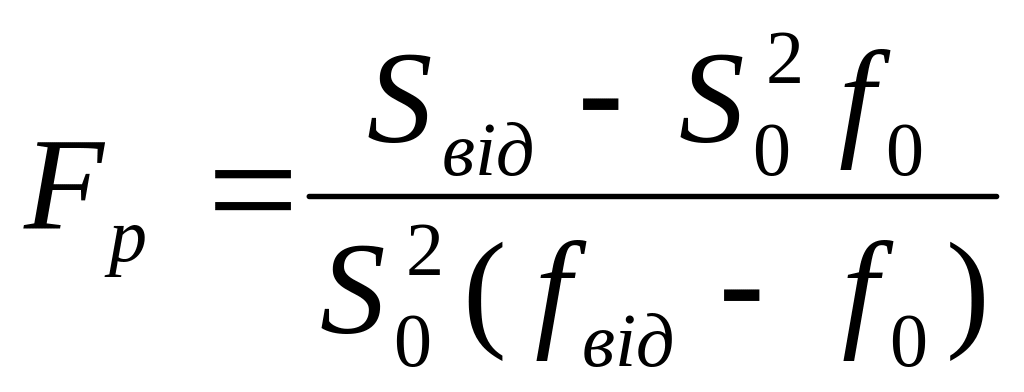
і порівнюють його з табличним для числа ступенів свободи f₀ = N₀ – 1; f_ад = f_від – f₀ і рівня значимості q. Якщо F_p ≤ F_T, то модель є адекватною. В такому випадку можна переходити до визначення координати оптимуму одним з пошукових методів або вирішити цю задачу аналітично з урахуванням необхідних та достатніх умов існування екстремуму.

Якщо нелінійна модель виявилася неадекватною, частіше за все в план вводять додаткові фактори і експеримент знову повторюють.

Приклад. При реалізації плану експерименту другого порядку на об’єкті дослідження і обробки результатів отримана адекватна нелінійна модель:

= 85,14 + 0,43х₁ + 0,32х₂ – 1,6х₁² – 1,19х₂² – 3х₁х₂ .

Треба знайти оптимальні умови роботи об’єкту.

Рішення. Необхідні умови існування екстремуму функції :

= 0,43 – 2*1,6х₁ – 3х₂; = 0,32 – 2*1,19х₂ – 3х₁ .

Вирішуємо цю систему рівнянь і знаходимо координати екстремуму:

х₁^* = - 0,0458; х₂^* = + 0,1922

Гесіан функції:

=

Кутовий мінор першого порядку Δ₁ є негативним (Δ₁ = - 3,2). Негативним є також визначник гесіану:

Δ = ( - 3,2)(- 2,38) – ( - 3)( - 3) = - 1,384.

Таким чином, в точці екстремуму спостерігається максимум цільової функції, абсолютна величина якого = 85,161.