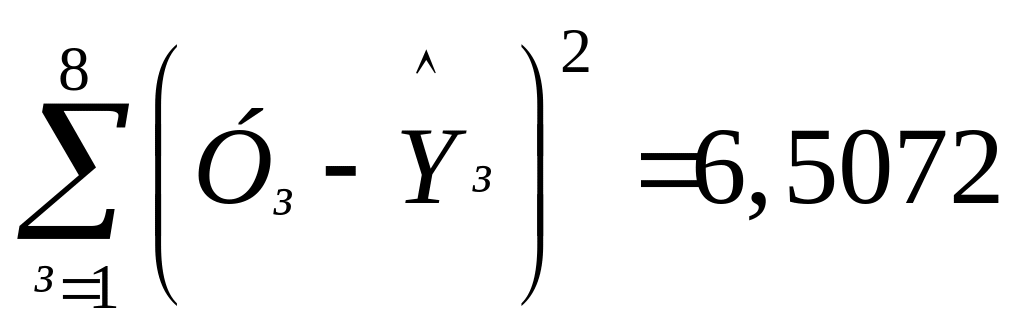5. Основний експеримент

Задачами основного експерименту є:

- отримання математичної моделі об’єкту дослідження у вигляді лінійної моделі;

- пошук оптимальної області функціонування об’єкту за лінійною моделлю;

- отримання математичної моделі об’єкту в області оптимуму у вигляді нелінійної моделі;

- пошук оптимальної координати функціонування об’єкту.

4.6.1. Факторний експеримент за планами першого порядку

Цей експеримент є першим етапом основного експерименту. Його сутність полягає в одночасному зміні всіх факторів, тобто параметрів об’єкту дослідження, за визначеним планом; репрезентації математичної моделі у вигляді лінійного поліному і дослідженні його методами математичної статистики.

Наведемо деякі основні терміни, які використовуються при подальшому розгляді матеріалу.

Рівнем фактору називають чітко визначене його значення, яке буде фіксуватися при проведенні експерименту. Наприклад, це температура 60 і 80⁰С або тиск 40 і 120Па та інше. Середні значення інтервалів зміни факторів називають нульовим рівнем. Для наведених прикладів це температура 70⁰С і тиск 80Па. Інтервал варіювання – це таке значення фактору в натуральних одиницях, тобто ⁰С, Па, кг, і т. д., додавання якого до нульового рівня дає верхній, а відіймання дає нижній рівень фактору. Для наведеного прикладу це температура 10⁰С і тиск 40Па. Верхній і нижній рівні фактору позначають символами " + 1” і “ – 1”, нульовий рівень “ 0 ”, що фактично відповідає кодуванню факторів за формулою:

,

де Х_і0 і Х_і – нульовий та фактичний рівень фактору;

ΔХ_і – інтервал його варіювання.

Експеримент, в якому реалізуються всі можливі сполучення рівнів факторів, називають повним факторним експериментом (ПФЕ). Якщо n факторів варіюють на двох рівнях, тобто на рівнях " + 1” і “ – 1”, то отримують ПФЕ типу 2ⁿ; якщо варіювання здійснюється на трьох рівнях ( + 1; 0; - 1), то кількість дослідів в такому повному факторному експерименті дорівнює 3ⁿ і т. д.

Загальні рекомендації до планування факторного експерименту першого порядку наступні:

- нульовий рівень плану бажано вибирати якомога ближче до оптимальної області. Це дозволить зменшити витрати часу і інших ресурсів на пошук оптимальної області при використанні отриманої лінійної моделі на другому етапі основного експерименту. Для такого вибору може бути використана апріорна інформація, результати попередніх експериментів на об’єкті або на лабораторній установці, досвід дослідника, знання фахівців та інше.

- інтервал варіювання фактору повинен перевищувати подвоєне середньоквадратичне відхилення даного параметра, тобто повинна дотримуватися нерівність:

2S_xi < ΔХ_і < (Х_{і max} – X_{i min}),

де (Х_{і max} – X_{i min}) - область визначення параметру Х_і.

В протилежному випадку на результати експерименту домінуючий вплив будуть чинити випадкові процеси і отримати адекватну модель буде неможливо. Значення середньоквадратичного відхилення беруть з результатів попередніх досліджень об’єкту.

Побудова матриці планування здійснюється із залученням прийому чергування знаків. Розглянемо цей прийом на прикладах складання планів повного факторного експерименту першого порядку для двох рівнів. Для двох факторів (n = 2) матриця в безрозмірних одиницях буде мати вигляд табл. 4.10 з загальною кількістю дослідів 2ⁿ = 2² = 4.

Таблиця 4.10

План ПФЕ першого порядку для n = 2

№№ дослідів	х0	х1	х2	yu1	yu2	…….
1	+1	+1	+1	y11	y12	…….
2	+1	-1	+1	y21	y22	…….
3	+1	+1	-1	y31	y32	…….
4	+1	-1	-1	y41	y42	…….

Для чотирьох факторів (n = 4) кількість дослідів буде складати 2⁴ = 16 і матриця плану буде мати вигляд табл. 4.11.

Таблиця 4.11

План ПФЕ першого порядку для n = 4

№№ дослідів	x0	х1	x2	х3	х4	yu1	yu2	…….	yu m
1	+1	+1	+1	+1	+1	y11	y12	…….	y1m
2	+1	-1	+1	+1	+1	y21	y22	…….	y2m
3	+1	+1	-1	+1	+1	y31	y32	…….	y3m
4	+1	-1	-1	+1	+1	y41	y42	…….	y4m
5	+1	+1	+1	-1	+1	y51	y52	…….	y5m
6	+1	-1	+1	-1	+1	y61	y62	…….	y6m
7	+1	+1	-1	-1	+1	y71	y72	…….	y7m
8	+1	-1	-1	-1	+1	y81	y82	…….	y8m
9	+1	+1	+1	+1	-1	y91	y92	…….	y9m
10	+1	-1	+1	+1	-1	y10 1	y10 2	…….	y10m
11	+1	+1	-1	+1	-1	y11 1	y11 2	…….	y11m
12	+1	-1	-1	+1	-1	y12 1	y12 2	…….	y12m
13	+1	+1	+1	-1	-1	y13 1	y13 2	…….	y13m
14	+1	-1	+1	-1	-1	y14 1	y14 2	…….	y14m
15	+1	+1	-1	-1	-1	y15 1	y15 2	…….	y15m
16	+1	-1	-1	-1	-1	y16 1	y16 2	…….	y16m

Тобто, за правилом чергування знаків в першому стовпчику знаки не змінюються. Це стовпчик фіктивної змінної х₀, який використовується при подальшій обробці результатів дослідів, зокрема, для визначення вільного члена рівняння регресії. Звичайно цей стовпчик в робочій матриці плану не наводять.

В другому стовпчику знаки змінюються почергово; в третьому – через 2; в четвертому – через 4 і так далі за показником ступенів 2.

Якщо рівень похибки в дослідах незначний у порівнянні зі значенням параметру, то план експерименту реалізують один раз і переходять до обробки експериментальних даних. Якщо в дослідах спостерігаються значні похибки, то виконують декілька (m) паралельних дослідів при однакових співвідношеннях факторів об’єкту, тобто, повторюють дослід m разів і знаходять середні значення вихідного параметру в кожному з цих дослідів, що дозволяє знизити похибку експерименту. (Як вже зазначалося раніш, за законом зростання точності в теорії випадкових помилок похибка “m” вимірів в разів менше, ніж похибка поодинокого виміру).

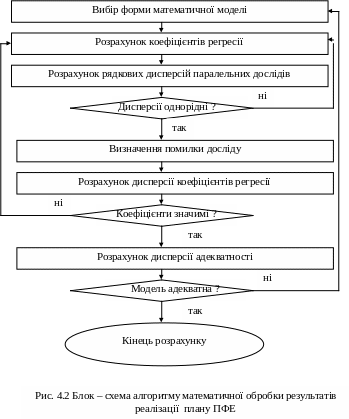
Розроблений план реалізують на об’єкті дослідження і починають обробку результатів експерименту. Алгоритм математичної обробки результатів реалізації плану ПФЕ представлений на рис. 4.2.

Розглянемо сутність кожного з етапів математичної обробки результатів дослідів. Як вже зазначалося, метою повного факторного експерименту першого порядку є отримання лінійної моделі у вигляді:

,

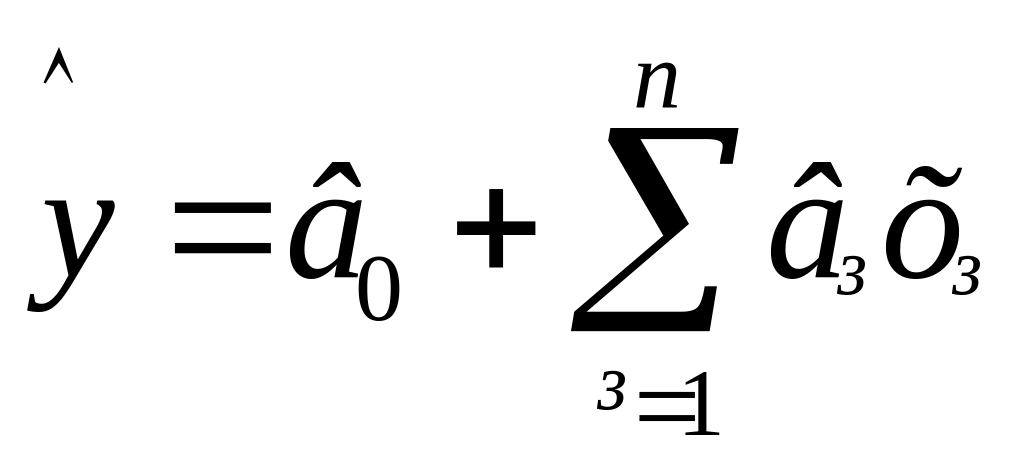де і = 1, 2,…, n – номери факторів, які впливають на вихідну змінну об’єкту у, тобто управляючі параметри об’єкту, значення яких можна стабілізувати на заданому рівні в кожному окремому досліді;

n – кількість факторів Х;

в₀ і в_і – коефіцієнти регресії.

Коефіцієнти рівняння регресії (так звані коефіцієнти лінійних ефектів) визначають за формулою:

,

де N – кількість рядків матриці планування (дослідів);

- середнє значення вихідного параметру (змінної стану) об’єкту досліджень за результатами m паралельних дослідів для u – того рядка матриці (тобто, при u – тому співвідношенні вхідних параметрів об’єкту).

Для вільного члена рівняння регресії використовується аналогічна формула:

,

або, оскільки х_0u = + 1, то його можна визначати як середнє значення вихідного параметру за результатами всіх дослідів:

.

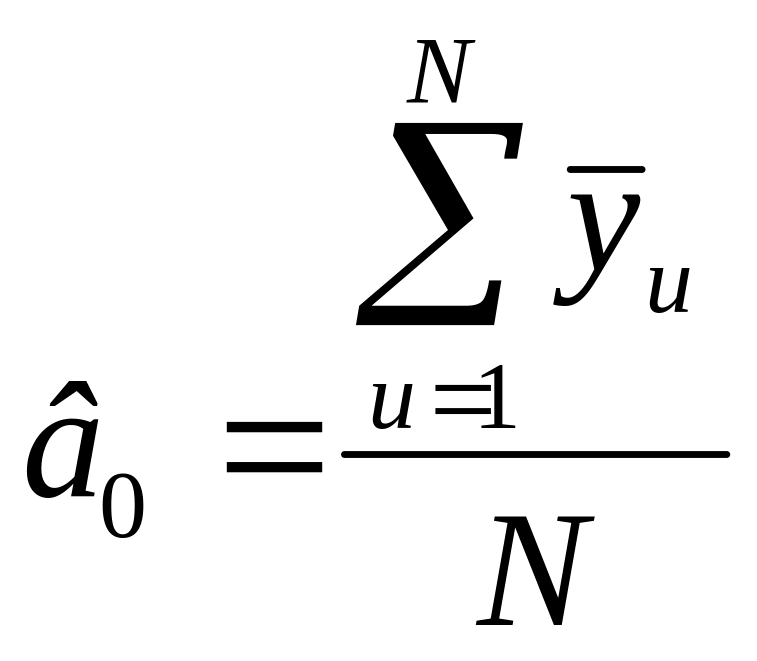Помилку досліду або дисперсію репродукції визначають за результатами паралельних дослідів. Для цього розраховують всі рядкові дисперсії за формулою:

,

знаходять їх суму, вибирають з них максимальну і розраховують критерій Кохрена:

G_p = .

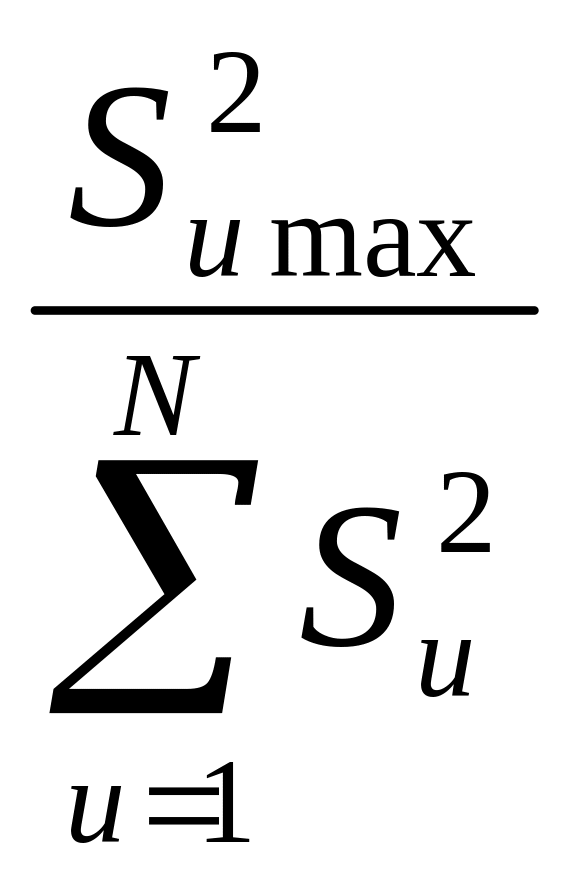Якщо розрахункове значення G_p менш, ніж табличне G_т (або дорівнює йому) для кількості ступенів свободи f₁ = m – 1; f₂ = N і рівня значимості q (звичайно 5%), то дисперсії вихідної змінної в дослідах є однорідними і їх можна усереднити за формулою:

.

Ця величина і є помилкою досліду.

В протилежному випадку, якщо G_p > G_т , треба збільшити кількість паралельних дослідів m. Таке може статися з різних причин: особливості властивостей об’єкту, його роботи, неуважність або недостатня кваліфікація експериментатора, недосконалість засобів експерименту. В останньому випадку інколи більш доцільно зробити заміну засобів проведення експерименту, ніж нарощувати кількість паралельних дослідів. Тобто, в кожній конкретній ситуації приймають відповідне рішення, яке б забезпечило досягнення прийнятного рівня відхилень дисперсій в кожному досліді від середніх значень. Неоднорідні рядкові дисперсії усереднювати неприпустимо.

Значимість коефіцієнтів регресії перевіряють наступним чином. Знаходять дисперсії коефіцієнтів за формулою:

і розраховують критерій Стьюдента:

Якщо t_pi перевищує або дорівнює табличному значенню критерію t_т для числа ступенів свободи f₀ = N(m – 1) і рівня значимості q , коефіцієнт регресії в_і є значимим і повинен бути присутнім в рівнянні регресії.

При невиконанні цієї умови, тобто при t_pi < t_т , відповідний коефіцієнт в_і повинен бути вилучений з рівняння.

Однак тут треба бути уважним і завжди пам’ятати, що в попередньому експерименті незначущі фактори вже відсіювалися. Тому отримана незначущість фактору може бути наслідком невдало вибраного інтервалу варіювання. Тобто може статися, що він був вибраний занадто малим і на результати вплинули домінуючим чином випадкові процеси. Звідси зрозуміло, що більш доречним є рішення повторити експеримент при розширеним інтервалі варіювання такого фактору. Звісно, при цьому кількість дослідів, а відповідно і витрати часу і ресурсів на проведення експерименту зростуть. Однак буде отримана більш об’єктивна оцінка властивостей об’єкту досліджень.

Інколи для зменшення експериментів половину результатів вже проведених дослідів зберігають за рахунок того, що розширення інтервалу виконується лише в один бік: або підвищують верхній рівень фактору, або знижують нижній рівень при стабільному іншому рівні.

Якщо фактор залишився незначущим і після повторення експерименту на розширеному інтервалі його варіювання, тоді його (або їх, якщо цих факторів декілька) впевнено відкидають і переходять до наступного етапу – до оцінки адекватності отриманої математичної моделі.

Для перевірки адекватності рівняння регресії порівнюють дві дисперсії – дисперсію адекватності і дисперсію репродукційності. Дисперсія адекватності показує розсіювання дослідних даних відносно розрахованих за рівнянням регресії :

,

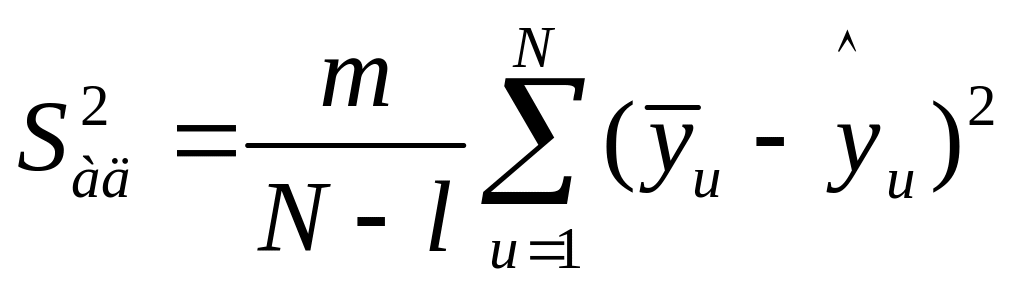де l – кількість членів в рівнянні регресії, які залишилися в ньому після оцінки значимості коефіцієнтів і відсіювання факторів, які є незначущими.

Адекватність моделі перевіряють за критерієм Фішера:

,

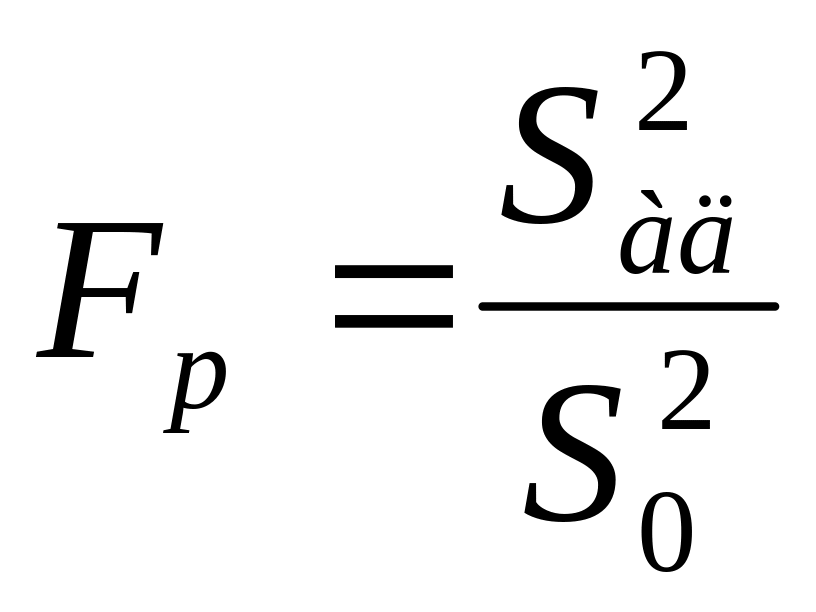який порівнюють з табличним його значенням F_т для числа ступенів свободи f_ад = N – l (для дисперсії адекватності); f₀ = N(m – 1) (для дисперсії досліду) і рівня значимості q.

При дотриманні співвідношення F_p ≤ F_т математична модель є адекватною. Це означає, що розсіювання експериментальних даних відносно рівняння регресії того ж порядку, що і розсіювання, яке викликане випадковими процесами в об’єкті. Таку адекватну модель можна використовувати для організації руху до області оптимуму з застосуванням, наприклад, градієнтного метода, метода крутого сходження, найшвидшого спуску та інше.

Перевірку адекватності за критерієм Фішера виконують, якщо дисперсія адекватності S_ад² є більшою, ніж помилка досліду S₀². Якщо за результатами експериментів отримано, що S_ад² ≤ S₀², то висновок про адекватність моделі можна зробити і без перевірки умови: F_p ≤ F_т .

Якщо лінійна модель виявляється неадекватною (F_p > F_т ), приймають рішення щодо змін в експерименті. Найбільш часто приймається рішення про зменшення інтервалів варіювання факторів і повторення експерименту. Таке рішення дозволяє зменшити кривизну поверхні відгуку змінної стану об’єкту. Однак при цьому зростає небезпека появи незначущих коефіцієнтів регресії, тому зменшення інтервалу треба робити в розумних, раціональних межах.

Інколи ефективним є включення до плану експерименту нового фактору з числа тих, котрі в попередньому експерименті були відсіяні, але були близькими за своїм ефектом до факторів, які залишилися в моделі. Застосовують також прийом переносу центру експерименту (нульової точки) в експериментальну точку найкращим значенням змінної стану, тобто вихідного параметру об’єкту, і повторення експерименту.

В разі неадекватності лінійної моделі і після застосування цих заходів або переходять до реалізації планів другого порядку, або здійснюють пошук оптимальної області за допомогою неадекватної моделі. Хоча це з математичної точки зору є некоректним, але на практиці такий ризик для досягнення результату часто є виправданим.

Приклад. За планом ПФЕ 2³ на камерній нагрівальній печі виконані дослідження впливу початкової температури металу на посаді Х₁, ⁰С, маси садки Х₂,т і питомої витрати повітря на спалювання палива Х₃, на середню продуктивність печі У, (табл. 4.12). Для оцінки помилки досліду в центрі плану додатково реалізовано 3 досліди. За нульовий рівень прийняті номінальні значення параметрів Х₁⁰ = 120⁰С; Х₂⁰ = 22т; Х₃⁰ = 12 ; інтервали їх варіювання: ΔХ₁ = 100⁰С; ΔХ₂ = 4т; ΔХ₃ = 2 . Виконати обробку дослідних даних.

Таблиця 4.12

План і результати експерименту, розрахункові дані

№№ дослідів	х0	Х1	х2	х3	У
1	+1	+1	+1	+1	9,86	10,91	1,1020
2	+1	-1	+1	+1	9,09	9,25	0,0256
3	+1	+1	-1	+1	6,35	6,61	0,0676
4	+1	-1	-1	+1	6,41	4,95	2,1320
5	+1	+1	+1	-1	15,00	13,73	1,6130
6	+1	-1	+1	-1	12,02	12,07	0,0025
7	+1	+1	-1	-1	9,48	9,43	0,0025
8	+1	-1	-1	-1	6,52	7,77	1,1562
9	+1	0	0	0	9,12
10	+1	0	0	0	10,30
11	+1	0	0	0	9,80

Рішення. Середнє значення продуктивності печі за N₀ = 3 дослідах в центрі плану і помилка досліду:

;

.

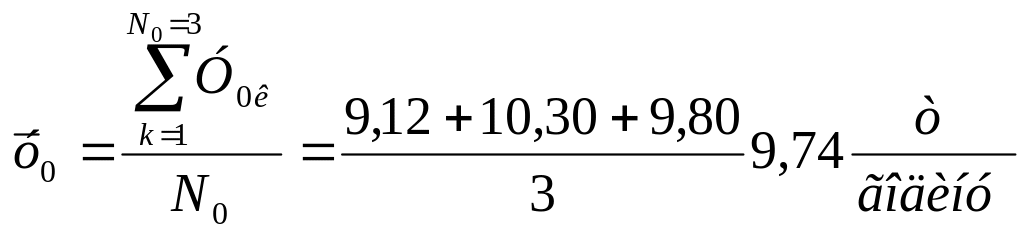За матрицею плану визначаємо:

; ; ; .

Коефіцієнти регресії:

; ; ; .

Рівняння регресії:

.

Дисперсія коефіцієнтів регресії і розрахунковий t – критерій для них:

; ; ; ; .

Табличне значення t – критерію для f = N₀ – 1 = 3 – 1 = 2 і q = 5% складає t_т = 4,3, що суттєво менш, ніж розрахункові значення t_і . Тобто всі коефіцієнти рівняння регресії є значимими.

За отриманим рівнянням розраховуємо прогнозовану продуктивність , відхилення дослідних даних від прогнозної лінії 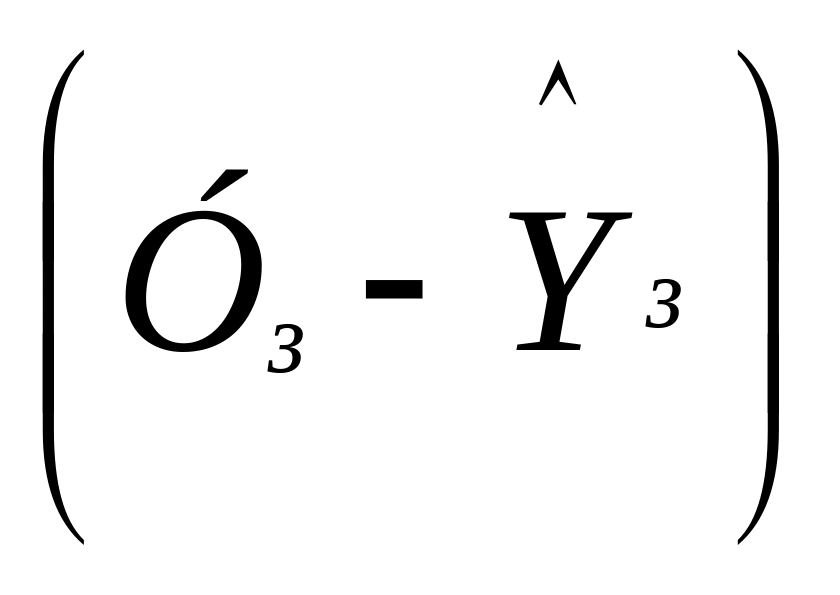і за сумою квадратів цих відхилень визначаємо дисперсію адекватності:

,

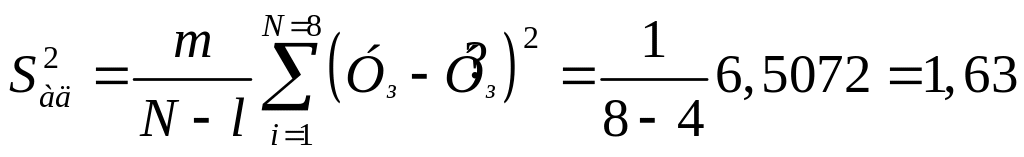де m = 1 – число паралельних дослідів при реалізації основного плану;

l = 4 – число членів у рівнянні регресії, які залишилися після перевірки значимості коефіцієнтів.

Критерій Фішера:

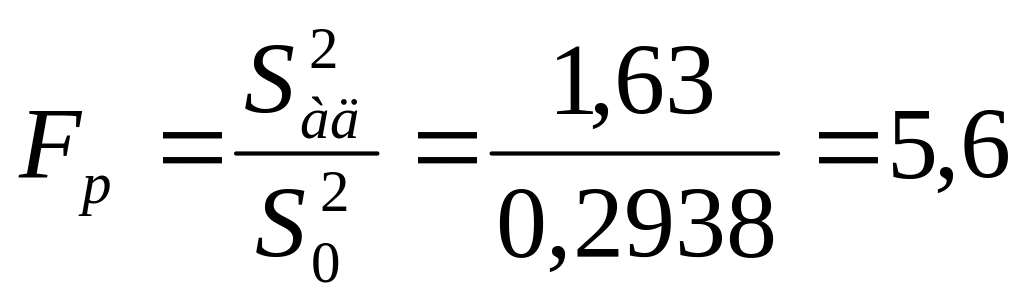
Табличне значення цього критерію для f_ад = N – l = 4; f₀ = N₀ – 1 = 2; q = 5% становить F_т = 19,25. Тому можна зробити висновок щодо адекватності отриманого лінійного рівняння.

В натуральному масштабі ця модель має наступний вигляд:

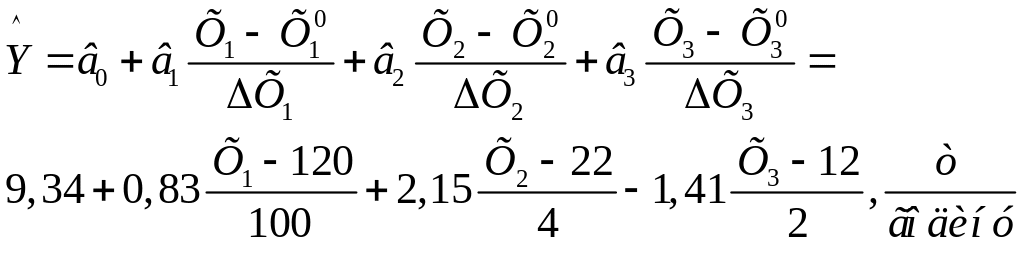
Результати реалізації ПФЕ першого порядку можна використати не лише для рішення задач оптимізації, а і для отримання апроксимаційних або інтерполяційних моделей об’єкту. Такі моделі мають вигляд:

,

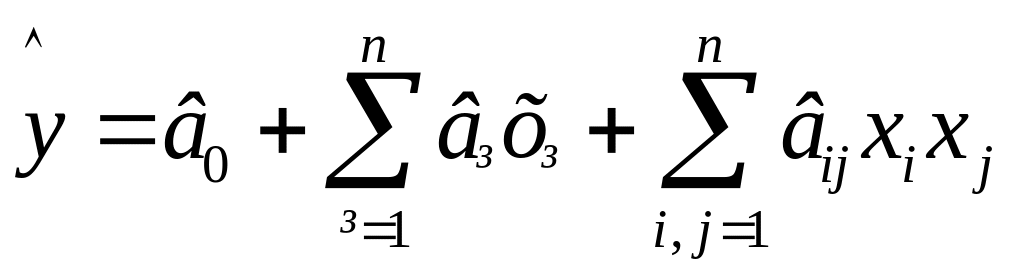де в_ij – коефіцієнти взаємодії факторів.

Для визначення коефіцієнтів взаємодії план ПФЕ доповнюють стовпчиками, які являють собою добуток стовпчиків відповідних факторів. Наприклад, для двохфакторного плану типу 2² розрахункова матриця має вигляд табл. 4.13.

Таблиця 4.13

Розрахункова матриця плану ПФЕ 2² для визначення ефектів взаємодії

№№ дослідів	х0	х1	х2	х1х2	yu1	yu2	…….
1	+1	+1	+1	+1	y11	y12	…….
2	+1	-1	+1	-1	y21	y22	…….
3	+1	+1	-1	-1	y31	y32	…….
4	+1	-1	-1	+1	y41	y42	…….

Коефіцієнти взаємодії визначають за формулою:

при х_і ≠ х_j

Наприклад, для наведеного плану модель має вигляд:

,

де .

Оцінка значимості коефіцієнтів взаємодії виконується за означеною раніш методикою, тобто, порівнянням розрахункового і табличного критерію Стьюдента для кожного з цих коефіцієнтів.